Input
n (0 < n < 20).
Output
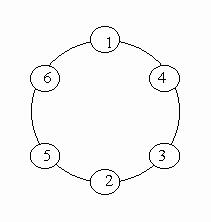
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
6
8
Sample Output
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
题意:输入一个数n,把1到n的自然数放到一个环里,保证相邻的两个数的和是素数。
二、解题思想
- dfs+素数打表
- 经典的一道DFS
三、代码
#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> using namespace std; const int maxn = 50; int a[maxn]; int b[maxn]; int n,prime[2*maxn]; bool vis[maxn]; //素数打表,相当于int prime[40]={0,1,1,1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,1,0,0}; void isprime() { int i,j; for(i = 0;i<50;i++) prime[i] = 1; prime[0] = prime[1] = 0; for(i = 2;i<50;i++) { if(prime[i]) for(j = i+i;j<50;j+=i) prime[j] = 0; } } //深搜 void dfs(int x) //x:当前搜索第几个数 { if(x==n+1 && prime[b[n]+b[1]]){ //满足条件了,就输出来 for(int i=1;i<n;i++) printf("%d ",b[i]); printf("%d\\n",b[n]); return; } for(int i=2;i<=n;i++){ if(!vis[i] && prime[a[i]+b[x-1]]){ //此数未用并且与上一个放到环中的数相加是素数 vis[i] = 1; //标记 b[x] = a [i]; //放进数组 dfs(x+1); vis[i] = 0; //退去标记 } } } int main() { int kase = 1; isprime(); while(cin>>n && (n>0&&n<20)){ for(int i=1;i<=n;i++) a[i] = i; memset(vis,0,sizeof(vis)); b[1] = 1; printf("Case %d:\\n",kase++); dfs(2); printf("\\n"); } return 0; }