求立方根算法--个人对立方根算法的穷举和优化
Posted GFuZan的博客
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了求立方根算法--个人对立方根算法的穷举和优化相关的知识,希望对你有一定的参考价值。
遇到了求立方根的题目,在此做一下算法笔记,
分析过程:
数n的立方根就是n=i*i*i;所以我们会优先想到一下方法.
static double g32(double n){ //简易版 double i = 0, k = 0.0005f; if (n < 0) { //输入负数判断 k /= -1; } do{ i+=k; }while(abs(i*i*i)<abs(n)); //abs为自己写的求绝对值方法 return i; }
可以看出此方法的求解精度为0.001;且当输入数据过大时效率堪忧,所以就有了以下优化
static double g33(double n){ //优化2 double i = 0, k = 5f; if (n < 0) { k /= -1; }for (int t = 0; t < 15; t++) {//精度到小数点后15位 do { i += k; //开始时每次加5快速逼近正确值 } while (abs(i * i * i) < abs(n)); //当i^3>=n时退出 i-=k;k /= 9.2; //i还原到退出前的值,k缩小,进入下一次逼近 } return i; }
此方法可以快速求得立方根,输入数值n不太大时使用,当n太大在逼近过程中i^3与(i+k)^3差距太大,循环次数剧增,进入死循环状态.在我电脑上当n=9999999999 (10个9)时就会进入死循环
所以想到一种解决方法,设置一循环次数计数器w,使k值随循环次数增加而增加,在一定程度上解决死循环问题.下面是代码
static double g34(double n){ //最终优化 double i = 0, k = 5f; if (n < 0) { k /= -1; } int w=0; for (int t = 0; t < 15; t++) { do { i += k; k=k+w*k/50000; w++; //循环计数器 } while (abs(i * i * i) < abs(n)); i-=k;k /= 9.5; } System.out.println(w); return i; }
更改后n等于20个9也不会死循环.
最后附上所有程序代码.
package com.gfuzan.test; import java.util.Scanner; public class Test { /** * 开发: GFuZan * 时间: 2017.08.08 * 功能: 立方根 */ public static void main(String[] args) { System.out.print("请输入一个数: "); Scanner sc = new Scanner(System.in); double n = sc.nextDouble(); sc.close(); System.out.println("Math: \\t"+ Math.pow(n, 1.0/3)); System.out.println("My简易版: \\t"+g32(n)); System.out.println("My优化2: \\t"+g33(n)); System.out.println("My最终优化:\\t"+g34(n)); } static double g32(double n){ //简易版 double i = 0, k = 0.0005f; if (n < 0) { k /= -1; } do{ i+=k; }while(abs(i*i*i)<abs(n)); return i; } static double g34(double n){ //最终优化 double i = 0, k = 5f; if (n < 0) { k /= -1; } int w=0; for (int t = 0; t < 15; t++) { do { i += k; k=k+w*k/50000; w++; } while (abs(i * i * i) < abs(n)); i-=k;k /= 9.5; } return i; } static double g33(double n){ //优化2 double i = 0, k = 5f; if (n < 0) { k /= -1; } for (int t = 0; t < 15; t++) { do { i += k; } while (abs(i * i * i) < abs(n)); i-=k;k /= 9.2; } return i; } static double abs(double f) { if (f < 0) { return 0 - f; } return f; } }
运行结果
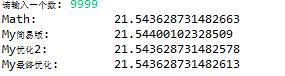
以上是关于求立方根算法--个人对立方根算法的穷举和优化的主要内容,如果未能解决你的问题,请参考以下文章