工作随笔

Posted 2020-10-01 longCC

测试题

ArrayList：

ArrayList是一种线性数据结构，它的底层是用数组实现的，相当于动态数组。与Java中的数组相比，它的容量能动态增长。类似于C语言中的动态申请内存，动态增长内存。 
当创建一个数组的时候，就必须确定它的大小，系统会在内存中开辟一块连续的空间，用来保存数组，因此数组容量固定且无法动态改变。ArrayList在保留数组可以快速查找的优势的基础上，弥补了数组在创建后，要往数组添加元素的弊端。实现的基本方法如下

1. 快速查找：在物理内存上采用顺序存储结构，因此可根据索引快速的查找元素。 
2. 容量动态增长

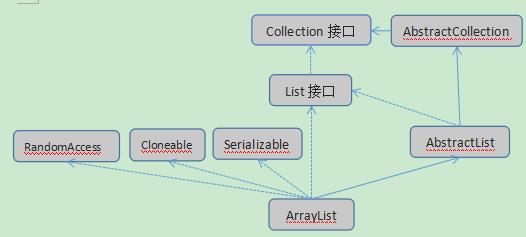
ArrayList与Collection关系如下图，实线代表继承，虚线代表实现接口： 

 

元素存储 
ArrayList是基于数组实现的，当添加元素的时候，如果数组大，则在将某个位置的值设置为指定元素即可，如果数组容量不够了，以add（E e）为例，可以看到add(E e)中先调用了ensureCapacity(size+1)方法，之后将元素的索引赋给elementData[size]，而后size自增。例如初次添加时，size为0，add将elementData[0]赋值为e，然后size设置为1（类似执行以下两条语句elementData[0]=e;size=1）。http://blog.csdn.net/jianyuerensheng/article/details/51192811

LinkedList

LinkedList与ArrayList一样，实现List接口，LinkedList是基于链表实现的，插入和删除操作比ArrayList更加有效，但随机访问的效率比ArrayList差。

LinedList数据结构原理：底层的数据结构是基于双向循环链表的，且头结点中不存放数据

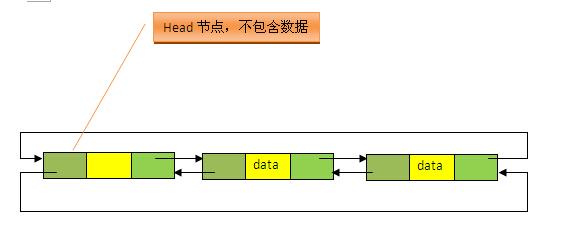
既然是双向链表，那么必定存在一种数据结构——我们可以称之为节点，节点实例保存业务数据，前一个节点的位置信息和后一个节点位置信息

stack：栈

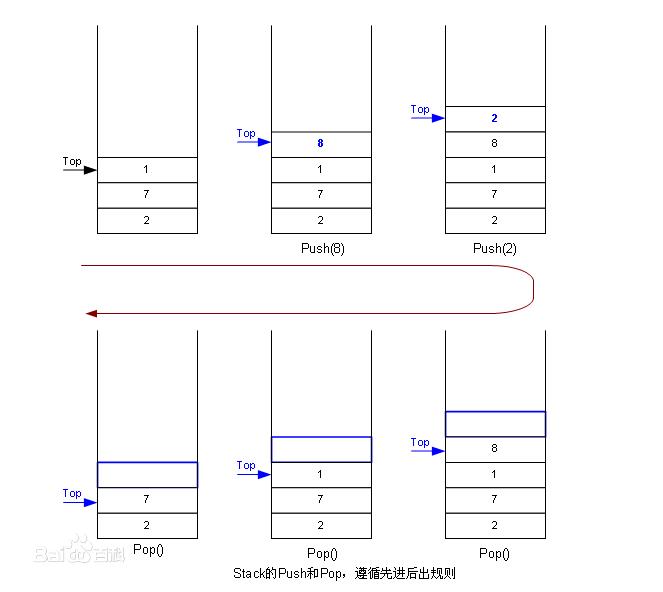
栈（stack）在计算机科学中是限定仅在表尾进行插入或删除操作的线性表。栈是一种数据结构，它按照后进先出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据。栈是只能在某一端插入和删除的特殊线性表。用桶堆积物品，先堆进来的压在底下，随后一件一件往上堆。取走时，只能从上面一件一件取。读和取都在顶部进行，底部一般是不动的。栈就是一种类似桶堆积物品的数据结构，进行删除和插入的一端称栈顶，另一端称栈底。插入一般称为进栈，删除则称为退栈。 栈也称为后进先出表。

 

Queue：队列

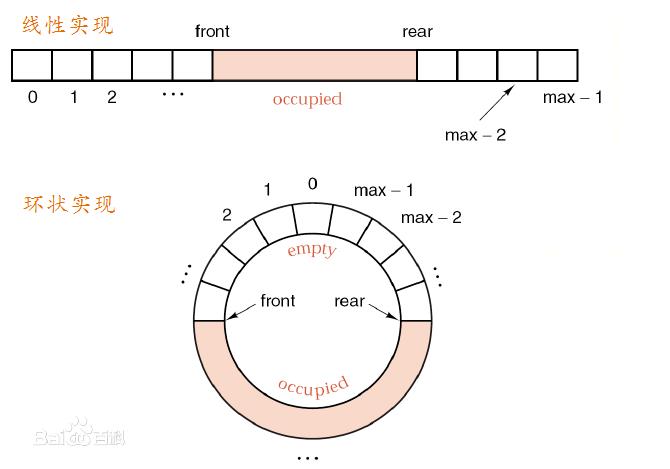
队列是一种特殊的线性表，是一种先进先出（FIFO）的数据结构。它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。

 

queue的基本操作有：

1.入队：如q.push(x):将x元素接到队列的末端；

2.出队：如q.pop() 弹出队列的第一个元素，并不会返回元素的值；

3,访问队首元素：如q.front()

4,访问队尾元素，如q.back();

5,访问队中的元素个数，如q.size();

成员函数

• q.empty()判断队列q是否为空，当队列q空时，返回true;否则为false（值为0(false)/1(true)）。
• q.size()访问队列q中的元素个数。(不可写成sizeof(q)或size（q）)
• q.push(a)会将一个元素a置入队列q中。
• q.front()会返回队列q内的第一个元素(也就是第一个被置入的元素)。(不可写成front(q))
• q.back()会返回队列q中最后一个元素(也就是最后被插入的元素)。(不可写成back(q))
• q.pop()会从队列q中移除第一个元素。(不可写成pop(q))[1] 
  注意：pop()虽然会移除下一个元素，但是并不返回它。
  front()和back()返回下一个元素但并不移除该元素。
  在stack库中的函数与queue很类似，但是stack中要返回元素时，只能返回最后一个元素，且函数名不一样（stack中为s.top()），需要区分。

Tree：树

 

树的标准定义：

 

树（tree）是包含n（n>0）个节点的有穷集合，其中：

 

　　（1）每个元素称为节点（node）；

 

　　（2）有一个特定的节点被称为根节点或树根（root）。

 

（3）除根节点之外的其余数据元素被分为m（m≥0）个互不相交的结合T1，T2，……Tm-1，其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）。

 

树具有以下特点：

 

（1）    每个节点有零个或多个子节点。

 

（2）    每个子节点只有一个父节点。

 

（3）    没有父节点的节点称为根节点。

关于树的一些术语

        节点的度：一个节点含有的子树的个数称为该节点的度；

        叶节点或终端节点：度为零的节点称为叶节点；

        非终端节点或分支节点：度不为零的节点；

        双亲节点或父节点：若一个结点含有子节点，则这个节点称为其子节点的父节点；

        孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；

        兄弟节点：具有相同父节点的节点互称为兄弟节点；

        树的高度或深度：定义一棵树的根结点层次为1，其他节点的层次是其父结点层次加1。一棵树中所有结点的层次的最大值称为这棵树的深度。节点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；

        树的度：一棵树中，最大的节点的度称为树的度；

        节点的祖先：从根到该节点所经分支上的所有节点；

        子孙：以某节点为根的子树中任一节点都称为该节点的子孙。

        森林：由m（m>=0）棵互不相交的树的集合称为森林；

二叉树：

二叉树首先是一棵树，每个节点都不能有多于两个的儿子，也就是树的度不能超过2。二叉树的两个儿子分别称为“左儿子”和“右儿子”，次序不能颠倒。如图1是一个简单的二叉树。

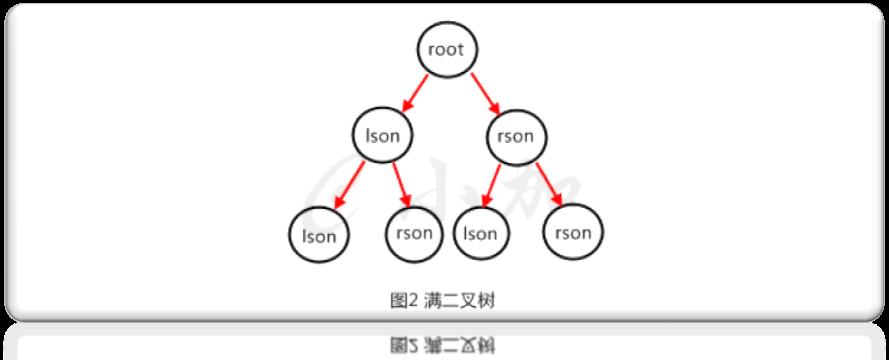
二叉树的遍历

二叉树的遍历有三种，分别为先序遍历，中序遍历和后序遍历。这三种遍历方式是根据根节点的读取顺序来分的：

先序遍历，就是最先读取根节点，然后再读取左子树（按照同样的方法读取子树上的节点），最后读取右子树；

中序遍历，就是第二个读取根节点，最先要读取的是左子树，然后根节点，最后右子树；

后序遍历，就是最后一个读取根节点，最先读取的是左子树，第二个读取右子树，最后读取根节点。

先序遍历的递归实现代码

Heap：堆

堆数据结构是一种数组对象，它可以被视为一科完全二叉树结构。它的特点是父节点的值大于（小于）两个子节点的值（分别称为大顶堆和小顶堆）。它常用于管理算法执行过程中的信息，应用场景包括堆排序，优先队列等。