数据结构学习笔记02堆栈

Posted 2020-06-27 kuotian

栈（stack）又名堆栈，它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。是一种后进先出（LIFO）的数据结构。

一．栈的顺序存储

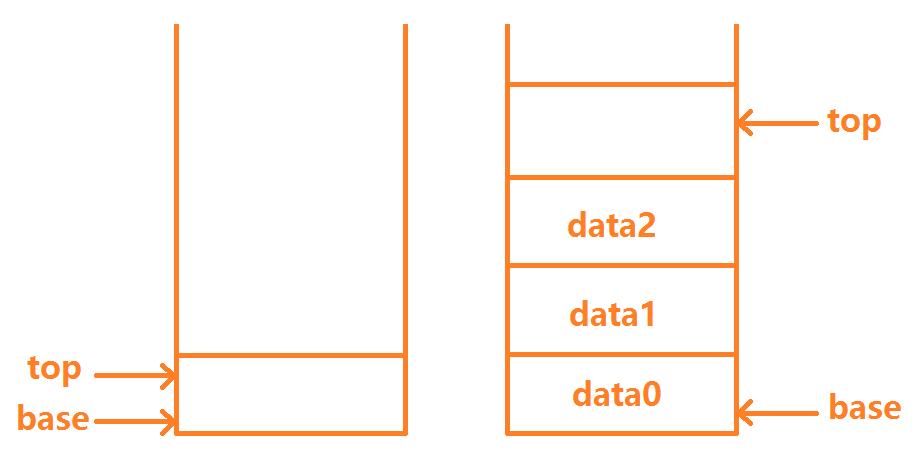
如图，左图为空栈，右图为已存放数据的栈。不难发现，栈只有一个口子，数据只能从一端进行入栈（push）和出栈（pop）操作。数据data的入栈顺序为 0， 1， 2.因此，出栈顺序只能为2,  1，0，从栈顶向栈底依次取出。

  1 //顺序栈
  2 #include <stdio.h>
  3 #include <stdlib.h>
  4 
  5 typedef int Status;
  6 typedef int SElemType; /* SElemType类型根据实际情况而定，这里假设为int */
  7 
  8 #define STACK_INTI_SIZE 100        //存储空间初始分配量 
  9 #define STACKINCREMENT 10        //存储空间分配增量
 10 
 11 #define OK 1
 12 #define ERROR 0
 13 #define INFEASIBLE -1
 14 #define OVERFLOW -2
 15 
 16 typedef struct {
 17     SElemType *base;    
 18     SElemType *top;        //栈顶指针
 19     int stacksize;        //当前已分配的存储空间
 20 }SqStack;
 21 
 22 Status InitStack(SqStack &S);    
 23 Status DestroyStack(SqStack &S);
 24 Status ClearStack(SqStack &S);
 25 bool StackEmpty(SqStack S);        
 26 int StackLength(SqStack S);            
 27 Status GetTop(SqStack S, SElemType &e);    
 28 Status Push(SqStack &S, SElemType e);    
 29 Status Pop(SqStack &S, SElemType &e);    
 30 Status StackTraverse(SqStack S, Status(*visit)(SElemType e));
 31 
 32 Status visit(SElemType c)
 33 {
 34     printf("%d ", c);
 35     return OK;
 36 }
 37 /*操作结果：构造一个空栈S*/ 
 38 Status InitStack(SqStack &S)
 39 {
 40     S.base = (SElemType *)malloc(STACK_INTI_SIZE * sizeof(SElemType));
 41     if (!S.base) exit(OVERFLOW);
 42     S.top = S.base;
 43     S.stacksize = STACK_INTI_SIZE;
 44     return OK;
 45 }
 46 /*初始条件：栈S已存在。
 47 操作结果：栈S被销毁*/ 
 48 Status DestroyStack(SqStack &S)
 49 {
 50     free(S.base);
 51     free(&S); 
 52     S.top = NULL;
 53     S.base = NULL;
 54     S.stacksize = 0;
 55     return OK;
 56 }
 57 /*初始条件：栈S已存在。
 58 操作结果：将S清为空栈*/ 
 59 Status ClearStack(SqStack &S)
 60 {
 61     S.top = S.base;
 62     return OK;
 63 }
 64 /*初始条件：栈S已存在。
 65 操作结果：若栈S为空栈，则返回TRUE，否则FALSE*/ 
 66 bool StackEmpty(SqStack S)
 67 {
 68     if (S.top == S.base)
 69         return true;
 70     else
 71         return false;
 72 }
 73 /*初始条件：栈S已存在。
 74 操作结果：返回S的元素个数，即栈的长度*/ 
 75 int StackLength(SqStack S)
 76 {
 77     return (S.top - S.base);
 78 }
 79 /*初始条件：栈S已存在且非空。
 80 操作结果：用e返回S的栈顶元素*/ 
 81 Status GetTop(SqStack S, SElemType &e)
 82 {
 83     if (S.top == S.base) return ERROR;    //若栈空 返回ERROR
 84     e = *(S.top - 1);
 85     return OK;
 86 }
 87 /*初始条件：栈S已存在。
 88 操作结果：插入元素e为新的栈顶元素*/ 
 89 Status Push(SqStack &S, SElemType e)
 90 {
 91     if (S.top - S.base >= S.stacksize) {        //栈满追加存储空间
 92         S.base = (SElemType *)realloc(S.base,     
 93                     (S.stacksize + STACKINCREMENT) * sizeof(SElemType));
 94         if (!S.base) exit(OVERFLOW);            //存储分配失败 
 95         S.top = S.base + S.stacksize;/*realloc可能返回了新的地址，所以top的地址需重新确定。*/ 
 96         S.stacksize += STACKINCREMENT;            //更新stacksize的值
 97     }
 98     *S.top++ = e;  //*S.top = e; S.top++
 99     return OK;
100 }
101 /*初始条件：栈S已存在且非空。
102 操作结果：删除S的栈顶元素，并用e返回其值*/ 
103 Status Pop(SqStack &S, SElemType &e)
104 {
105     if (S.top == S.base) return ERROR;
106     e = * --S.top;  //S.top--; e = *S.top;
107     return OK;
108 }
109 /*初始条件：栈S已存在且非空。
110 操作结果：从栈底到栈顶依次对S的每个数据元素调用函数visit()。
111 一旦visit()失败，则操作失败。*/ 
112 Status StackTraverse(SqStack S, Status(*visit)(SElemType e))
113 {
114     if (S.base == S.top)
115     {
116         printf("栈为空！");
117         return ERROR;
118     }
119     for (SElemType *p = S.base;p < S.top;p++)
120         visit(*p);
121     
122     printf("\\n");
123     return OK;
124 }
125 int main()
126 {
127     SqStack s;
128     int e,length;
129     
130     if (InitStack(s) == OK)
131         for (int j = 1;j <= 10;j++)
132             Push(s, j);
133     length = StackLength(s);
134     StackTraverse(s,visit);
135     printf("length = %d\\n", length);
136     if (StackEmpty(s) == true)
137         printf("empty!\\n");
138     else printf("not empty!\\n");
139     Pop(s, e);
140     printf("e = %d\\n", e);
141     ClearStack(s);
142     if (StackEmpty(s) == true)
143         printf("empty!\\n");
144     else printf("not empty!\\n");
145     DestroyStack(s);
146     if (StackEmpty(s) == true)
147         printf("empty!\\n");
148     else printf("not empty!\\n");
149     system("pause");
150     return 0;
151 }

sj2_0

栈的顺序存储表示:

#define STACK_INTI_SIZE 100            //存储空间初始分配量

#define STACKINCREMENT 10           //存储空间分配增量

typedef struct {

       SElemType *base;        //在栈构造之前和销毁之后，base值为NULL

       SElemType *top;          //栈顶指针

       int stacksize;         //当前已分配的存储空间

}SqStack;

顺序栈的基本操作：/*只需浏览，作了解，详情（代码：sj2_0）*/

Status InitStack(SqStack &S);     

       操作结果：构造一个空栈S。

Status DestroyStack(SqStack &S);

       初始条件：栈S已存在。

　　  操作结果：栈S被销毁。

Status ClearStack(SqStack &S);

       初始条件：栈S已存在。

　　  操作结果：将S清为空栈

Status StackEmpty(SqStack S);   

       初始条件：栈S已存在。

　　  操作结果：若栈S为空栈，则返回TRUE，否则FALSE。

int StackLength(SqStack S);       

       初始条件：栈S已存在。

　　  操作结果：返回S的元素个数，即栈的长度。

Status GetTop(SqStack S, SElemType &e);

　　  初始条件：栈S已存在且非空。

　　  操作结果：用e返回S的栈顶元素。

Status Push(SqStack &S, SElemType e);    

       初始条件：栈S已存在。

　　  操作结果：插入元素e为新的栈顶元素。

Status Pop(SqStack &S, SElemType &e);   

　　  初始条件：栈S已存在且非空。

　　  操作结果：删除S的栈顶元素，并用e返回其值。

Status StackTraverse(SqStack S, Status(*visit)(SElemType e));

       初始条件：栈S已存在且非空。

　　  操作结果：从栈底到栈顶依次对S的每个数据元素调用函数visit()。

　　  一旦visit()失败，则操作失败。

1.入栈操作

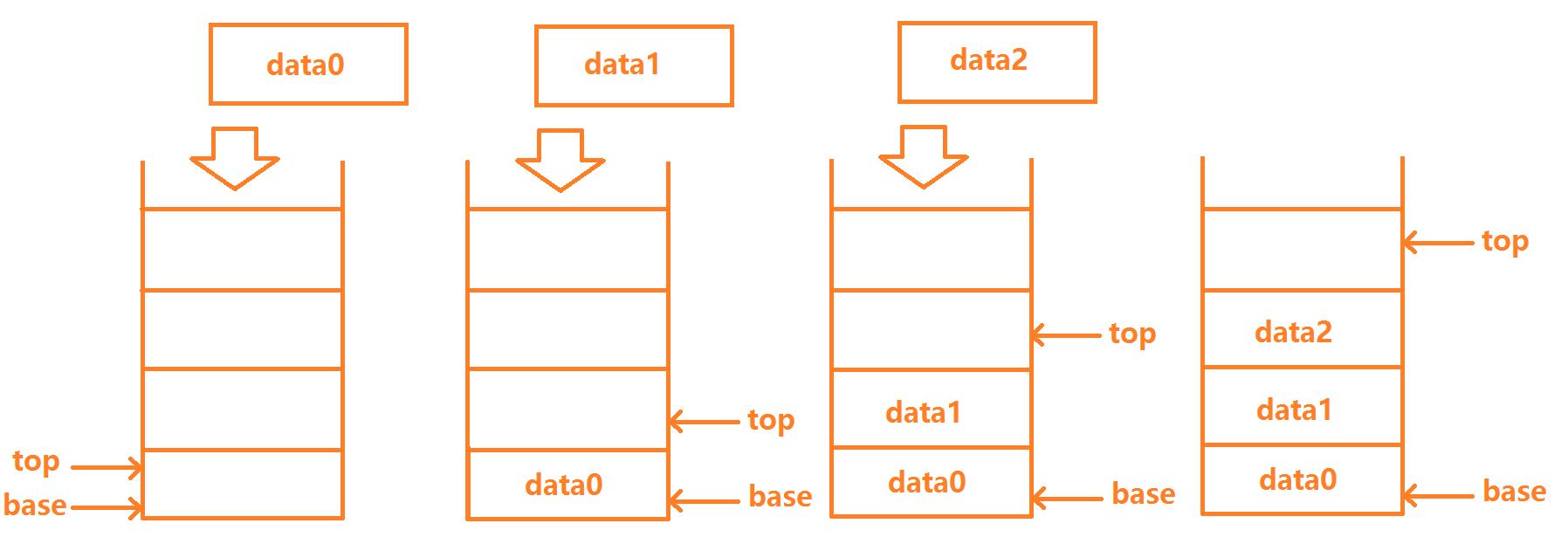
　　算法思路：

　　1. *top = e

　　2. top++

　　3.若栈满用realloc追加空间

　　//malloc、calloc、realloc的区别　　http://www.cnblogs.com/kuotian/p/5277335.html

 1 /*初始条件：栈S已存在。
 2 操作结果：插入元素e为新的栈顶元素*/ 
 3 Status Push(SqStack &S, SElemType e)
 4 {
 5     if (S.top - S.base >= S.stacksize) {        //栈满追加存储空间
 6         S.base = (SElemType *)realloc(S.base,     
 7                     (S.stacksize + STACKINCREMENT) * sizeof(SElemType));
 8         if (!S.base) exit(OVERFLOW);            //存储分配失败 
 9         S.top = S.base + S.stacksize;/*realloc可能返回了新的地址，所以top的地址需重新确定。*/ 
10         S.stacksize += STACKINCREMENT;            //更新stacksize的值
11     }
12     *S.top++ = e;  //*S.top = e; S.top++
13     return OK;
14 }

View Code

 

2.出栈操作

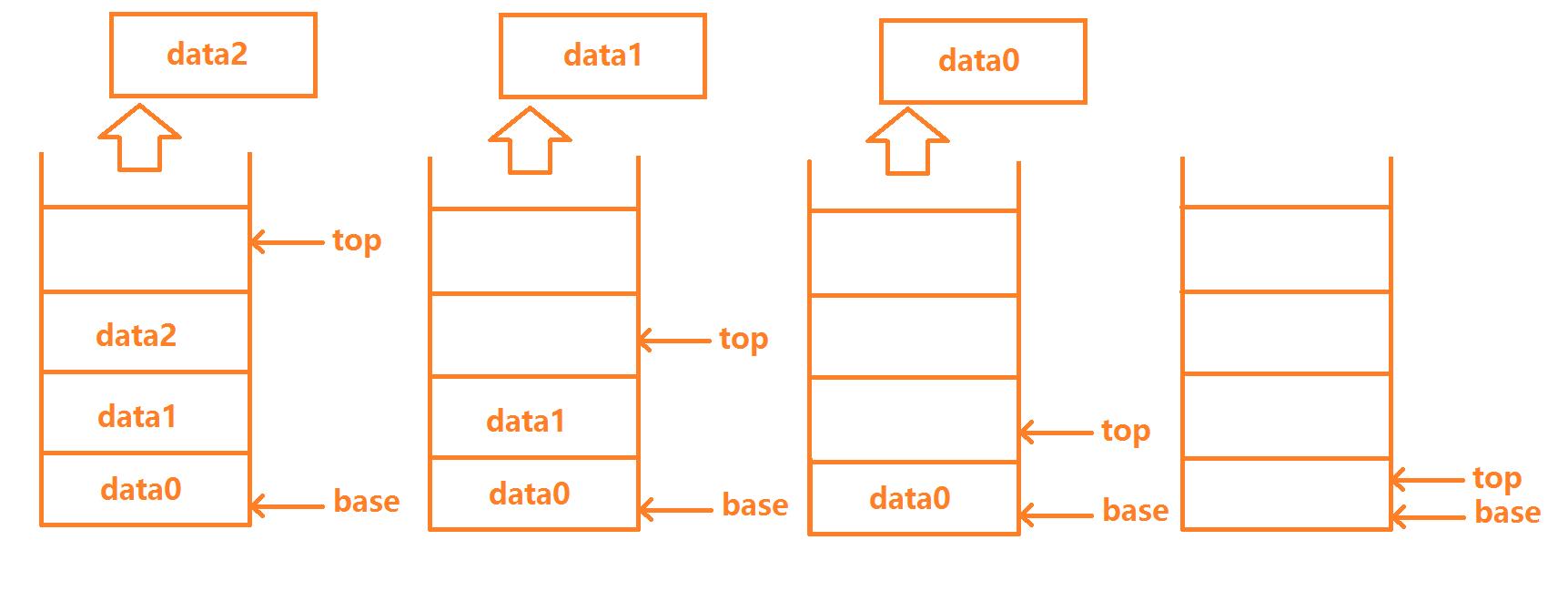
　　算法思路：

　　1.若top == base 即栈为空，不能pop，返回ERROR。

　　2.top—

　　3.e = *top

1 /*初始条件：栈S已存在且非空。
2 操作结果：删除S的栈顶元素，并用e返回其值*/ 
3 Status Pop(SqStack &S, SElemType &e)
4 {
5     if (S.top == S.base) 
6             return ERROR;
7     e = * --S.top;  //S.top--; e = *S.top;
8     return OK;
9 }        

View Code

 

practice：

1.假设以顺序存储结构实现一个双向栈，即在一维数组的存储空间中存在着两个栈，他们的栈底分别设在数组的两个端点。试编写实现这个双向栈tws的三个操作：初始化inistack(tws)、入栈push(tws,I,x)和出栈pop(tws,i)的算法，其中i为0或1，用以分别指示设在数组两端的两个栈，并讨论按过程(正/误状态变量可设为变参)或函数设计这些操作算法各有说明优缺点。(代码：sj2_1)

  1 /*顺序存储结构双向栈 */
  2 #include <stdio.h>
  3 #include <stdlib.h>
  4 
  5 typedef int Status;
  6 typedef int SElemType; /* SElemType类型根据实际情况而定，这里假设为int */
  7 
  8 #define OK 1
  9 #define ERROR 0
 10 #define INFEASIBLE -1
 11 #define OVERFLOW -2
 12 
 13 #define MAXSIZE 100
 14 
 15 #define LEFT 1
 16 #define RIGHT 0
 17 typedef struct
 18 {
 19     SElemType data[MAXSIZE];
 20     int top1;    /* 栈1栈顶 */
 21     int top2;    /* 栈2栈顶 */
 22 }SqDoubleStack;
 23 
 24 Status InitStack(SqDoubleStack &S);
 25 Status DestroyStack(SqDoubleStack &S);
 26 Status ClearStack(SqDoubleStack &S);
 27 bool StackEmpty(SqDoubleStack S);
 28 int StackLength(SqDoubleStack S, int flag);
 29 Status GetTop(SqDoubleStack S, SElemType &e,int flag);
 30 Status Push(SqDoubleStack &S, SElemType e, int flag);
 31 Status Pop(SqDoubleStack &S, SElemType &e, int flag);
 32 Status StackTraverse(SqDoubleStack S, Status(*visit)(SElemType e),int flag);
 33 
 34 Status visit(SElemType c)
 35 {
 36     printf("%d ", c);
 37     return OK;
 38 }
 39 
 40 Status InitStack(SqDoubleStack &S)
 41 {
 42     S.top1 = -1;
 43     S.top2 = MAXSIZE;
 44     return OK;
 45 }
 46 
 47 Status DestroyStack(SqDoubleStack &S)
 48 {
 49     S.top1 = -1;
 50     S.top2 = -1;
 51 //    S.top1 = NULL;
 52 //    S.top2 = NULL;
 53     return OK;
 54 }
 55 
 56 Status ClearStack(SqDoubleStack &S)
 57 {
 58     S.top1 = -1;
 59     S.top2 = MAXSIZE;
 60     return OK;
 61 }
 62 
 63 bool StackEmpty(SqDoubleStack S)
 64 {
 65     if (S.top1 == -1 && S.top2 == MAXSIZE)
 66         return true;
 67     else
 68         return false;
 69 }
 70 
 71 int StackLength(SqDoubleStack S, int flag)
 72 {
 73     if (flag == LEFT)
 74         return (S.top1 + 1);
 75     else
 76         return (MAXSIZE - S.top2);
 77 }
 78 Status GetTop(SqDoubleStack S, SElemType &e, int flag)
 79 {
 80     if (flag == LEFT)
 81         e = S.data[S.top1];
 82     else
 83         e = S.data[S.top2];
 84     return OK;
 85 }
 86 
 87 Status Push(SqDoubleStack &S, SElemType e, int flag)
 88 {
 89     if (S.top1 + 1 == S.top2)
 90         return ERROR;
 91     if (flag == LEFT)
 92         S.data[++S.top1] = e;
 93     else
 94         S.data[--S.top2] = e;
 95     return OK;
 96 }
 97 
 98 Status Pop(SqDoubleStack &S, SElemType &e, int flag)
 99 {
100     if (flag == LEFT) {
101         if (S.top1 == -1) return ERROR;
102         else
103             e = S.data[S.top1--];
104 
105     }
106     else {
107         if (S.top2 == MAXSIZE) return ERROR;
108         else
109             e = S.data[S.top2++];
110     }
111     return OK;
112 }
113 
114 Status StackTraverse(SqDoubleStack S, Status(*visit)(SElemType e),int flag)
115 {
116     int i;
117     if (flag == LEFT)
118     {
119         for (i = 0;i <= S.top1;i++) 
120             visit(S.data[i]);
121     }
122     else
123     {
124         for (i = MAXSIZE - 1;i >= S.top2;i--) 
125             visit(S.data[i]);
126     }
127     printf("\\n");
128     return OK;
129 }
130 
131 int main()
132 {
133     SqDoubleStack s;
134     int e;
135     InitStack(s);
136     
137     Push(s, 2, 1);
138     Push(s, 7, 1);
139     Push(s, 3, 0);
140     Push(s, 5, 0);
141     Push(s, 5, 0);
142     
143     StackTraverse(s, visit, 1);
144     StackTraverse(s, visit, 0);
145     system("pause");
146     return 0;
147 }

sj2_1

 

二.链栈

栈的链式表示如图，栈的操作是线性表操作的特例。(代码: sj2_2)

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 #define OK 1
 5 #define ERROR 0
 6 
 7 
 8 typedef int Status;
 9 typedef int ElementType; /* SElemType类型根据实际情况而定，这里假设为int */
10 
11  
12 struct SNode{
13     ElementType data;
14     struct SNode *next;
15 };
16 typedef struct SNode *PtrToSNode;//PtrToSNode指向结点的指针
17 typedef PtrToSNode Stack;//Stack指向结点的指针 
18 
19 Stack CreateStack();
20 bool IsEmpty(Stack S);
21 bool Push(Stack S, ElementType X);
22 ElementType Pop(Stack S);
23 
24 /* 构建一个堆栈的头结点，返回该结点指针 */
25 Stack CreateStack() 
26 { 
27     Stack S;
28     S = (PtrToSNode)malloc(sizeof(struct SNode));
29     S->next = NULL;
30     return S;
31 }
32 /* 判断堆栈S是否为空，若是返回true；否则返回false */
33 bool IsEmpty(Stack S)
34 { 
35     return ( S->next == NULL );
36 }
37 
38 /* 将元素X压入堆栈S */
39 bool Push(Stack S, ElementType X)
40 { 
41     PtrToSNode tmpCell;
42     tmpCell = (PtrToSNode)malloc(sizeof(struct SNode));
43     tmpCell->data = X;
44     tmpCell->next = S->next;
45     S->next = tmpCell;
46     return true;
47 }
48 
49 /* 删除并返回堆栈S的栈顶元素 */
50 ElementType Pop(Stack S)  
51 { 
52     PtrToSNode firstCell;
53     ElementType topElem;
数据结构学习笔记——顺序存储结构实现栈

 堆栈的定义和两种存储结构下堆栈的基本操作
 数据结构学习笔记——链式存储结构实现栈
 数据结构学习笔记——链式存储结构实现栈（链栈）
 数据结构学习笔记——队列的基本知识和顺序存储结构实现队列
 栈的顺序存储和链式存储