AVL树
Posted 未夏
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了AVL树相关的知识,希望对你有一定的参考价值。

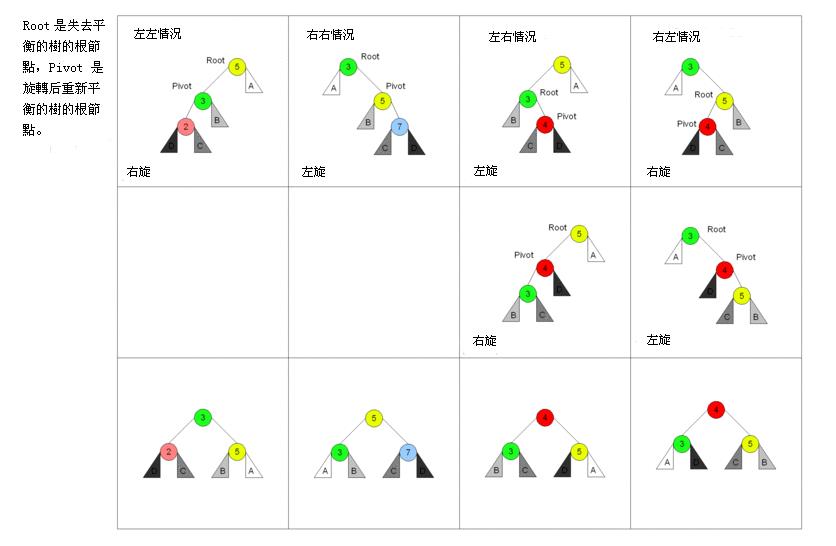
C实现代码如下:
1 2 /* 3 AVL树 4 */ 5 6 /*接口头文件*/ 7 typedef int ElementType; 8 9 #ifndef _AVLTREE_H 10 #define _AVLTREE_H 11 12 struct AVLNode; 13 typedef struct AVLNode * PtrToNode; 14 typedef PtrToNode Position; 15 typedef PtrToNode AVLTree; 16 17 /*操作集*/ 18 AVLTree MakeEmpty( AVLTree T ); 19 AVLTree Insert( ElementType X, AVLTree T ); 20 AVLTree Delete( ElementType X, AVLTree T ); 21 Position Find( ElementType X, AVLTree T ); 22 Position FindMin( AVLTree T ); 23 Position FindMax( AVLTree T ); 24 ElementType Retrieve( Position P ); 25 void PrintfTree( AVLTree T ); 26 27 #endif 28 29 30 /*接口实现*/ 31 #include <stdio.h> 32 #include <stdlib.h> 33 #include "AVLTree.h" 34 35 /*特定结构体定义*/ 36 struct AVLNode 37 { 38 ElementType Element; 39 AVLTree Left; 40 AVLTree Right; 41 int Height; 42 }; 43 44 int Height( Position P ); 45 int Max( int A, int B ); 46 Position SingleRotateWithLeft( Position K1 ); 47 Position SingleRotateWithRight( Position K1 ); 48 Position DoubleRotateWithLeft( Position K1 ); 49 Position DoubleRotateWithRight( Position K1 ); 50 51 AVLTree 52 MakeEmpty( AVLTree T ) 53 { 54 if ( T != NULL ) 55 { 56 MakeEmpty( T->Left ); 57 MakeEmpty( T->Right ); 58 MakeEmpty( T ); 59 } 60 61 return NULL; 62 } 63 64 Position 65 Find( ElementType X, AVLTree T ) 66 { 67 if ( T == NULL ) 68 return NULL; 69 if ( X < T->Element ) 70 return Find( X, T->Left ); 71 else 72 if ( X > T->Right ) 73 return Find( X, T->Right ); 74 else 75 return T; 76 } 77 78 /*递归例程*/ 79 Position 80 FindMin( AVLTree T ) 81 { 82 if ( T == NULL ) 83 return NULL; 84 if ( T->Left == NULL ) 85 return T; 86 else 87 return FindMin( T->Left ); 88 } 89 90 /*非递归例程*/ 91 /* 92 Position 93 FindMin( AVLTree T 0 94 { 95 if ( T != NULL ) 96 while ( T->Left != NULL ) 97 T = T->Left; 98 99 return T; 100 } 101 */ 102 103 /*递归例程*/ 104 Position 105 FindMax( AVLTree T ) 106 { 107 if ( T == NULL ) 108 return NULL; 109 if ( T->Right == NULL ) 110 return T; 111 else 112 return FindMax( T->Right ); 113 } 114 115 /*非递归例程*/ 116 /* 117 Position 118 FindMax( AVLTree T ) 119 { 120 if ( T != NULL ) 121 while ( T->Right 1= NULL ) 122 T = T->Right; 123 124 return T; 125 } 126 */ 127 128 ElementType 129 Retrieve( Position P ) 130 { 131 return P->Element; 132 } 133 134 /*中序查找,打印*/ 135 void 136 PrintfTree( AVLTree T ) 137 { 138 if ( T != NULL ) 139 { 140 PrintfTree( T->Left ); 141 printf( "%3d", T->Element ); 142 PrintfTree( T->Right ); 143 } 144 } 145 146 AVLTree 147 Insert( ElementType X, AVLTree T ) 148 { 149 if ( T == NULL ) 150 { 151 T = ( AVLTree )malloc( sizeof( struct AVLNode ) ); 152 if ( T == NULL ) 153 { 154 printf( "No Space!!!\\n" ); 155 exit( 1 ); 156 } 157 T->Element = X; 158 T->Height = 0; 159 T->Left = NULL; 160 T->Right = NULL; 161 } 162 163 if ( X < T->Element ) 164 { 165 T->Left = Insert( X, T->Left ); 166 if ( Height( T->Left ) - Height( T->Right ) == 2 ) 167 { 168 if ( X < T->Left->Element ) 169 T = SingleRotateWithLeft( T ); 170 else 171 T = DoubleRotateWithLeft( T ); 172 } 173 } 174 else 175 if ( X > T->Element ) 176 { 177 T->Right = Insert( X, T->Right ); 178 if ( Height( T->Right ) - Height( T->Left ) == 2 ) 179 { 180 if ( X > T->Right->Element ) 181 T = SingleRotateWithRight( T ); 182 else 183 T = DoubleRotateWithRight( T ); 184 } 185 } 186 187 T->Height = Max( Height( T->Left ), Height( T->Right ) ) + 1; 188 189 return T; 190 } 191 192 int 193 Max( int A, int B ) 194 { 195 return A > B ? A : B; 196 } 197 198 int 199 Height( Position P ) 200 { 201 if ( P == NULL ) 202 return -1; 203 else 204 return Max( Height( P->Left ), Height( P->Right ) ) + 1; 205 } 206 207 Position 208 SingleRotateWithLeft( Position K1 ) 209 { 210 Position K2 = K1->Left; 211 212 K1->Left = K2->Right; 213 K2->Right = K1; 214 215 /*update height*/ 216 K1->Height = Height( K1 ); 217 K2->Height = Height( K2 ); 218 219 return K2; 220 } 221 222 Position 223 SingleRotateWithRight( Position K1 ) 224 { 225 Position K2 = K1->Right; 226 227 K1->Right = K2->Left; 228 K2->Left = K1; 229 230 /*update height*/ 231 K1->Height = Height( K1 ); 232 K2->Height = Height( K2 ); 233 234 return K2; 235 } 236 237 Position 238 DoubleRotateWithLeft( Position K1 ) 239 { 240 Position K2 = K1->Left; 241 Position K3 = K2->Right; 242 243 K1->Left = SingleRotateWithRight( K2 ); 244 return SingleRotateWithLeft( K1 ); 245 } 246 247 Position 248 DoubleRotateWithRight( Position K1 ) 249 { 250 Position K2 = K1->Right; 251 Position K3 = K2->Left; 252 253 K1->Right = SingleRotateWithLeft( K2 ); 254 return SingleRotateWithRight( K1 ); 255 } 256 257 258 /*AVLTree 259 Insert( ElementType X, AVLTree T ) 260 { 261 if ( T == NULL ) 262 { 263 T = ( AVLTree )malloc( sizeof( struct AVLNode ) ); 264 if ( T == NULL ) 265 { 266 printf( "No Space!!!\\n" ); 267 exit( 1 ); 268 } 269 T->Element = X; 270 T->Left = NULL; 271 T->Right = NULL; 272 } 273 else if ( X < T->Element ) 274 T->Left = Insert( X, T->Left ); 275 else if ( X > T->Element ) 276 T->Right = Insert( X, T->Right ); 277 278 return T; 279 }*/
以上是关于AVL树的主要内容,如果未能解决你的问题,请参考以下文章