HDU——3501 Calculation 2

Posted 2020-10-01

题意：

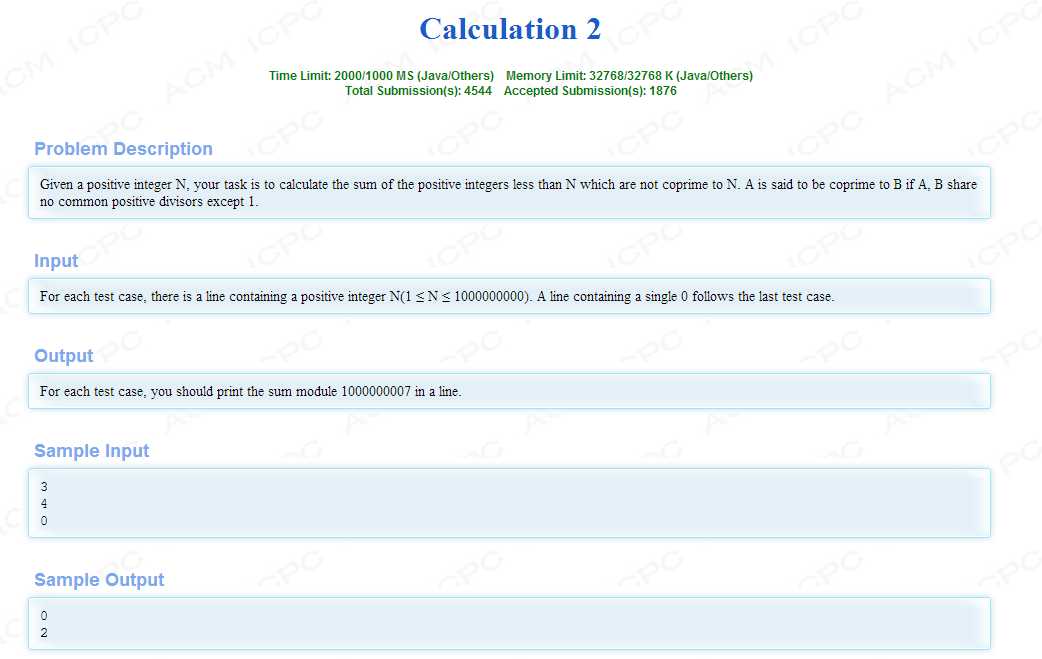
给定正整数n，求所有小于n的且与n为非互质数的和。
输入
对于每一个测试用例，都有一个包含正整数n(1≤n≤1000000000)的行。包含单个0的行将遵循最后一个测试用例。
输出
对于每个测试用例，您应该在一行中打印求和模1000000007。

思路：

考虑互质的数的一个性质，n与m互质，那么m-n与m也一定互质。

好，我们再来考虑这个题。

让求与n为非互质数的数的和，那么我们是不是就可以先把所有数的和求出来然后再减去与n互质的数的和？？？！！

好，我们就这样干。 有人又要问了，为什么要这样啊，不是更麻烦吗？？！！

好像不是这样的，因为我们可以用欧拉函数求与n互质的数的个数啊！！这样我们就不用暴力枚举了啊。。。

（好像知道与n互质的数的个数也没有用啊。。。）

(⊙o⊙)…      我们考虑数学里的小技巧。再求n内所有数的和时，我们是不是可以用等差数列前n项和公式？？（公式是什么。。。）

等差数列求和公式                  s=n*（n-1）/2

好，这样我们就轻松求出n以内所有数的和了。 我们接下来再求与n互质的数的和。（怎么求？？）

我们继续看上面给出的性质，一共有phi（n）个与n互质的数，而且这phi（n）个数一定存在m、n-m的关系，那么这两个数两两相加不就是n吗？？我们可以凑出phi（n）/2对n，这样这phi（n）个数的和不就是n*phi(n)/2吗？？！！

好了，这样我们就完工了。。。。

代码：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define mod 1000000007
using namespace std;
int t,n;
long long ans;
int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘) f=-1; ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘) {x=x*10+ch-‘0‘; ch=getchar();}
    return x*f;
}
int get_phi(int x)
{
    int sum=x;
    if(x%2==0) 
    {
        while(x%2==0) x/=2;
        sum/=2;
    }
    for(int i=3;i*i<=x;i+=2)
    {
        if(x%i==0)
        {
           while(x%i==0) x/=i;
           sum=sum/i*(i-1);    
        }
    }
    if(x>1) sum=sum/x*(x-1);
    return sum;
}
int main()
{
    while(1)
    {
        n=read();
        if(n==0) break;
        ans=(long long )n*(n-1)/2;
        ans-=(long long )n*get_phi(n)/2;
        printf("%lld\\n",ans%mod);
    }
    return 0;
}