散列表链地址法查找成功的平均查找长度怎么计算

Posted 2023-05-18

一、举个例子：数组长度10 散列函数x%7。

如 13 先计算散列 13%7 = 6 如果没有冲突的话会被放在第六个格子里。

现在散列表中 ： (x为已经有一个元素 o表示空)

0 x

1 x

2 x

3 o

4 o

5 x

6 x

7 x

8 x

9 o

计算失败概率 ： 

思路如下，任意出现一个数字（概率均等）经过hash函数以后 0 ~ 6的概率均等 现在假设 输入一个数字 hash计算结果是1，去1里查找，结果发现位置1(接下来简称pos1)不是目标元素（查找失败），于是线性探查找到了2（还是失败）然后找三，发现没有，于是确定所找元素不在哈希表里。

以上是查找过程，以此类推失败的情况下需要找 4，3，2，1，1，5，4 （7和7以后没得找，因为任何数膜7都<7）失败概率。

二、查找不成功的次数表如下表所示

Key 7 8 30 11 18 9 14

Count 3 2 1 2 1 5 

所以ASLunsuccess= （3+2+1+2+1+5+4）/ 7 = 18/7。

扩展资料：

散列函数

在进行查找时，在记录的存储位置与它的关键字之间建立一个确定的对应关系h,以线性表中每个元素的关键字K为自变量，通过函数h(K)计算出该元素的存储位置，我们将h函数称为散列函数或哈希函数。h(K)的值称为散列地址或哈希地址。

例：

假定一个线性表为A=(18,75,60,43,54,90,46)，选取散列函数为：

h(K)=K%m 取m=13

则得每个元素散列地址：

h(18)=18 % 13=5 h(75)=75 % 13=10 h(60)=60 % 13=8 h(43)=43 % 13=4

h(54)=54 % 13=2 h(90)=90 % 13=12 h(46)=46 % 13=7

参考资料来源:百度百科-散列查找

参考技术A 举个例子吧 数组长度10 散列函数x%7
如 13 先计算散列 13%7 = 6 如果没有冲突的话会被放在第六个格子里
现在散列表中 ： (x为已经有一个元素 o表示空)
0 x
1 x
2 x
3 o
4 o
5 x
6 x
7 x
8 x
9 o

计算失败概率 ： 思路如下，任意出现一个数字（概率均等）经过hash函数以后 0 ~ 6的概率均等 现在假设 输入一个数字 hash计算结果是1，去1里查找，结果发现位置1(接下来简称pos1)不是目标元素（查找失败），于是线性探查找到了2（还是失败）然后找三，发现没有，于是确定所找元素不在哈希表里，以上是查找过程，以此类推失败的情况下需要找 4，3，2，1，1，5，4 （7和7以后没得找，因为任何数膜7都<7）失败概率 参考技术B 举个例子吧 数组长度10 散列函数x%7
如 13 先计算散列 13%7 = 6 如果没有冲突的话会被放在第六个格子里
现在散列表中 ： (x为已经有一个元素 o表示空)
0 x
1 x
2 x
3 o
4 o
5 x
6 x
7 x
8 x
9 o

计算失败概率 ： 思路如下，任意出现一个数字（概率均等）经过hash函数以后 0 ~ 6的概率均等 现在假设 输入一个数字 hash计算结果是1，去1里查找，结果发现位置1(接下来简称pos1)不是目标元素（查找失败），于是线性探查找到了2（还是失败）然后找三，发现没有，于是确定所找元素不在哈希表里，以上是查找过程，以此类推失败的情况下需要找 4，3，2，1，1，5，4 （7和7以后没得找，因为任何数膜7都<7）失败概率~~~自己算吧~本回答被提问者和网友采纳

散列表

一、基本概念

关键字的全域为集合U，待散列的关键字集合为K，散列表的存储需求为O(K)，同时针对平均情况的查找时间为O(1)。关键字k被存放在槽h(k)中，即利用散列函数h，由关键字k计算出槽的位置，h将U映射到散列表T[0...m1]的槽位上。

冲突：两个关键字可能映射到同一个槽中。

解决冲突：链接法、开放寻址法

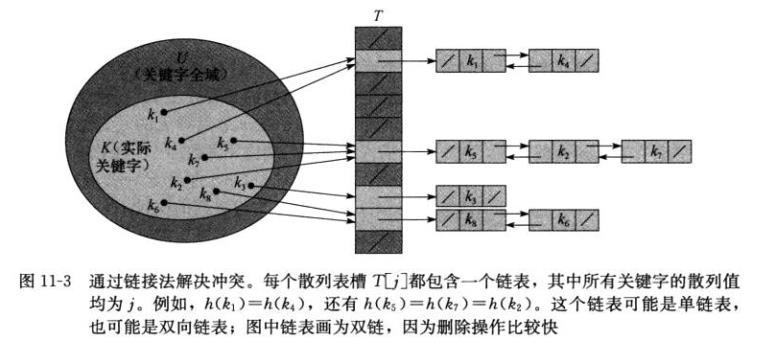
二、通过链接法解决冲突

把散列到同一槽中的所有元素都放在一个链表中，如下图所示。

 

 

  1 /* 通过链接法解决冲突的散列表
  2    链接链表，使用双向、非循环、非排序方式
  3 */
  4 #include <stdio.h>
  5 #include <stdlib.h>
  6 
  7 #define HASH_SIZE 10
  8 #define ARRAY_SIZE 15
  9 
 10 typedef struct object {
 11     int key;
 12     struct object *prev,*next;
 13 }object_s;
 14 
 15 typedef struct chainedhash {
 16     object_s *ptable[HASH_SIZE];
 17 }chainedhash_s;
 18 
 19 //函数声明
 20 void chained_hash_init(chainedhash_s *phash);
 21 void chained_hash_insert(chainedhash_s *phash, int key);
 22 object_s *chained_hash_search(chainedhash_s *phash, int key);
 23 void chained_hash_delete(chainedhash_s *phash, object_s *pobj);
 24 void chained_hash_print(chainedhash_s *phash);
 25 int hash_function(int key);
 26 
 27 int main(void)
 28 {
 29     chainedhash_s hash;
 30     int index;    
 31         
 32     chained_hash_init(&hash);
 33     
 34     for(index=0;index<ARRAY_SIZE; index++) {
 35          chained_hash_insert(&hash, index);
 36     }
 37     
 38     chained_hash_print(&hash);
 39     return 0;
 40 }
 41 
 42 void chained_hash_init(chainedhash_s *phash)
 43 {
 44     int i;
 45     for(i=0; i<HASH_SIZE; i++)
 46         phash->ptable[i] = NULL;
 47 }
 48 
 49 void chained_hash_insert(chainedhash_s *phash, int key)
 50 {
 51     object_s *pobj;
 52     int index;
 53     
 54     pobj = (object_s*)malloc(sizeof(object_s));
 55     pobj->key = key;
 56     index = hash_function(key);
 57     
 58     // 从链表头插入
 59     if(phash->ptable[index] != NULL)
 60         phash->ptable[index]->prev = pobj;
 61     pobj->prev = NULL;
 62     pobj->next = phash->ptable[index];
 63     phash->ptable[index] = pobj;
 64     
 65     return;
 66 }
 67 
 68 object_s *chained_hash_search(chainedhash_s *phash, int key)
 69 {
 70     int index;
 71     object_s *pobj;
 72     
 73     index = hash_function(key);
 74     for(pobj=phash->ptable[index]; pobj!=NULL; pobj=pobj->next) {
 75         if(pobj->key == key)
 76             return pobj;
 77     }
 78         
 79     return NULL;
 80 }
 81 
 82 void chained_hash_delete(chainedhash_s *phash, object_s *pobj)
 83 {
 84     int index;
 85     index = hash_function(pobj->key);
 86     
 87     if(phash->ptable[index] == pobj) {
 88         phash->ptable[index] = pobj->next;
 89         if(pobj->next != NULL)
 90             pobj->next->prev = NULL;
 91     } else {
 92         pobj->prev->next = pobj->next;
 93         if(pobj->next != NULL)
 94             pobj->next->prev = pobj->prev;
 95     }
 96     free(pobj);
 97 }
 98 
 99 void chained_hash_print(chainedhash_s *phash)
100 {
101     int index;
102     object_s *pobj;
103     
104     for(index=0; index<HASH_SIZE; index++) {
105         printf("%d:",index);
106         for(pobj=phash->ptable[index]; pobj!=NULL; pobj=pobj->next) {
107             printf("%d ",pobj->key);
108         }
109         printf("\\n");
110     }
111 }
112 
113 int hash_function(int key)
114 {
115     return key%10;
116 }

 三、开放寻址法解决冲突

在开放寻址法中，当要插入一个元素时，可以连续地检查（或称探查）散列表的各项，直到找到一个空槽来放置待插入的关键字时为止。在必须删除关键字的应用中，往往采用链表法来解决碰撞。若采用一致散列，则search、insert时间复杂度都为O(1)

探查序列有三种

1.线性探查。 h(k,i)=(h\'(k) + i) mod m, i=0,1,...,m-1 ；m种不同的探查序列

2.二次探查。 h(k,i) = (h\'(k) + c1*i + c*i^2) mod m ； m种不同的探查序列

3.双重散列。h(k,i) = (h1(k) + i*h2*k)) mod m ； m^2种不同的探查序列

 

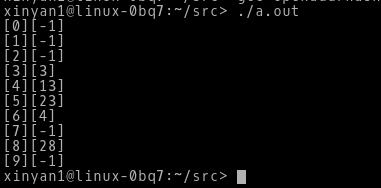
 1 // 散列表，使用开发寻址法（线性探测）解决冲突
 2 #include<stdio.h>
 3 
 4 #define HASH_SIZE 10
 5 #define ARRAY_SIZE 5
 6 #define FAIL -1
 7 
 8 int hashtable[HASH_SIZE];
 9 
10 // 函数声明
11 int insert_hash(int hasht[], int key);
12 int search_hash(int hasht[], int key);
13 void init_hash(int hasht[]);
14 int hash_function(int key, int i);
15 
16 int main(void)
17 {
18     int array[ARRAY_SIZE]={3,13,23,4,28};
19     int i;
20     
21     init_hash(hashtable);
22     
23     for(i=0;i<ARRAY_SIZE;i++)
24         insert_hash(hashtable, array[i]);
25     
26     for(i=0; i<HASH_SIZE; i++)
27         printf("[%d][%d]\\n",i,hashtable[i]);
28 }
29 
30 int insert_hash(int hasht[], int key)
31 {
32     int i,j;
33 
34     for(i=0;i<HASH_SIZE;i++) {
35         j=hash_function(key, i);
36         if(hasht[j] == -1) {
37             hasht[j]=key;
38             return j;
39         }
40     }
41     printf("hash table overflow\\n");
42     return FAIL;
43 }
44 
45 int search_hash(int hasht[], int key)
46 {
47     int i,j;
48     
49     for(i=0; i<HASH_SIZE; i++) {
50         j=hash_function(key, i);
51         if(hasht[j] == key) {
52             return j;
53         }
54         if(-1 == hasht[j])
55             break;
56     }
57     
58     return FAIL;
59 }
60 
61 void init_hash(int hasht[])
62 {
63     int i;
64     for(i=0; i<HASH_SIZE; i++)
65         hasht[i]=-1;
66 }
67 
68 int hash_function(int key, int i)
69 {
70     return (key%HASH_SIZE+i)%HASH_SIZE;
71 }

测试结果如下：