目录
一、引例
1、一类不等式组的解
二、最短路
1、Dijkstra
2、图的存储
3、链式前向星
4、Dijkstra + 优先队列
5、Bellman-Ford
6、SPFA
7、Floyd-Warshall
三、差分约束
1、数形结合
2、三角不等式
3、解的存在性
4、最大值 => 最小值
5、不等式标准化
四、差分约束的经典应用
1、线性约束
2、区间约束
3、未知条件约束
五、差分约束题集整理
一、引例
1、一类不等式组的解
给定n个变量和m个不等式,每个不等式形如 x[i] - x[j] <= a[k] (0 <= i, j < n, 0 <= k < m, a[k]已知),求 x[n-1] - x[0] 的最大值。例如当n = 4,m = 5,不等式组如图一-1-1所示的情况,求x3 - x0的最大值。
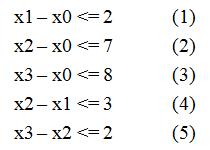
图一-1-1
1. (3) x3 - x0 <= 8
2. (2) + (5) x3 - x0 <= 9
3. (1) + (4) + (5) x3 - x0 <= 7
这里的T等于{8, 9, 7},所以min{ T } = 7,答案就是7。的确是7吗?我们再仔细看看,发现的确没有其它情况了。那么问题就是这种方法即使做出来了还是带有问号的,不能确定正确与否,如何系统地解决这类问题呢?
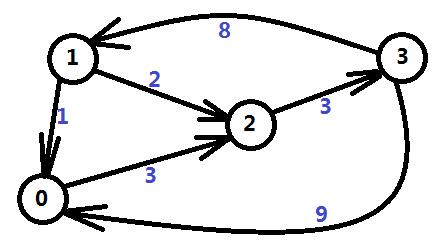
让我们来看另一个问题,这个问题描述相对简单,给定四个小岛以及小岛之间的有向距离,问从第0个岛到第3个岛的最短距离。如图一-1-2所示,箭头指向的线段代表两个小岛之间的有向边,蓝色数字代表距离权值。


图一-1-2
这个问题就是经典的最短路问题。由于这个图比较简单,我们可以枚举所有的路线,发现总共三条路线,如下:
1. 0 -> 3 长度为8
2. 0 -> 2 -> 3 长度为7+2 = 9
3. 0 -> 1 -> 2 -> 3 长度为2 + 3 + 2 = 7
最短路为三条线路中的长度的最小值即7,所以最短路的长度就是7。这和上面的不等式有什么关系呢?还是先来看看最短路求解的原理,看懂原理自然就能想到两者的联系了。
二、最短路
1、Dijkstra
最短路满足最优子结构性质,所以是一个动态规划问题。最短路的最优子结构可以描述为:
D(s, t) = {Vs ... Vi ... Vj ... Vt}表示s到t的最短路,其中i和j是这条路径上的两个中间结点,那么D(i, j)必定是i到j的最短路,这个性质是显然的,可以用反证法证明。
基于上面的最优子结构性质,如果存在这样一条最短路D(s, t) = {Vs ... Vi Vt},其中i和t是最短路上相邻的点,那么D(s, i) = {Vs ... Vi} 必定是s到i的最短路。Dijkstra算法就是基于这样一个性质,通过最短路径长度递增,逐渐生成最短路。
Dijkstra算法是最经典的最短路算法,用于计算正权图的单源最短路(Single Source Shortest Path,源点给定,通过该算法可以求出起点到所有点的最短路),它是基于这样一个事实:如果源点到x点的最短路已经求出,并且保存在d[x] ( 可以将它理解为D(s, x) )上,那么可以利用x去更新 x能够直接到达的点 的最短路。即:
d[y] = min{ d[y], d[x] + w(x, y) } y为x能够直接到达的点,w(x, y) 则表示x->y这条有向边的边权
具体算法描述如下:对于图G = <V, E>,源点为s,d[i]表示s到i的最短路,visit[i]表示d[i]是否已经确定(布尔值)。
1) 初始化 所有顶点 d[i] = INF, visit[i] = false,令d[s] = 0;
2) 从所有visit[i]为false的顶点中找到一个d[i]值最小的,令x = i; 如果找不到,算法结束;
3) 标记visit[x] = true, 更新和x直接相邻的所有顶点y的最短路: d[y] = min{ d[y], d[x] + w(x, y) }
(第三步中如果y和x并不是直接相邻,则令w(x, y) = INF)
2、图的存储
以上算法的时间复杂度为O(n^2),n为结点个数,即每次找一个d[i]值最小的,总共n次,每次找到后对其它所有顶点进行更新,更新n次。由于算法复杂度是和点有关,并且平方级别的,所以还是需要考虑一下点数较多而边数较少的情况,接下来以图一-2-1为例讨论一下边的存储方式。

图一-2-1
邻接矩阵是直接利用一个二维数组对边的关系进行存储,矩阵的第i行第j列的值 表示 i -> j 这条边的权值;特殊的,如果不存在这条边,用一个特殊标记来表示;如果i == j,则权值为0。它的优点是实现非常简单,而且很容易理解;缺点也很明显,如果这个图是一个非常稀疏的图,图中边很少,但是点很多,就会造成非常大的内存浪费,点数过大的时候根本就无法存储。图一-2-2展示了图一-2-1的邻接矩阵表示法。


图一-2-2
邻接表是图中常用的存储结构之一,每个顶点都有一个链表,这个链表的数据表示和当前顶点直接相邻的顶点(如果边有权值,还需要保存边权信息)。邻接表的优点是对于稀疏图不会有数据浪费,缺点就是实现相对麻烦,需要自己实现链表,动态分配内存。图一-2-3展示了图一-2-1的邻接表表示法。

图一-2-3
前向星是以存储边的方式来存储图,先将边读入并存储在连续的数组中,然后按照边的起点进行排序,这样数组中起点相等的边就能够在数组中进行连续访问了。它的优点是实现简单,容易理解,缺点是需要在所有边都读入完毕的情况下对所有边进行一次排序,带来了时间开销,实用性也较差,只适合离线算法。图一-2-4展示了图一-2-1的前向星表示法。
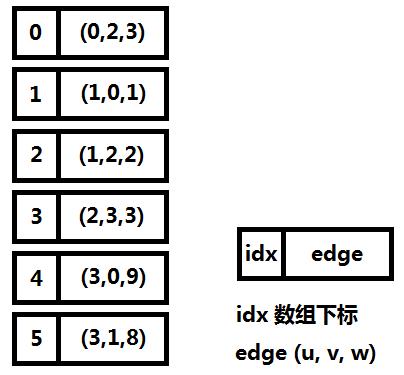
图二-2-4
那么用哪种数据结构才能满足所有图的需求呢?这里介绍一种新的数据结构一一链式前向星。
3、链式前向星
链式前向星和邻接表类似,也是链式结构和线性结构的结合,每个结点i都有一个链表,链表的所有数据是从i出发的所有边的集合(对比邻接表存的是顶点集合),边的表示为一个四元组(u, v, w, next),其中(u, v)代表该条边的有向顶点对,w代表边上的权值,next指向下一条边。
具体的,我们需要一个边的结构体数组 edge[MAXM],MAXM表示边的总数,所有边都存储在这个结构体数组中,并且用head[i]来指向 i 结点的第一条边。
边的结构体声明如下:
struct EDGE {
int u, v, w, next;
EDGE() {}
EDGE(int _u, int _v, int _w, int _next) {
u = _u, v = _v, w = _w, next = _next;
}
}edge[MAXM];
int u, v, w, next;
EDGE() {}
EDGE(int _u, int _v, int _w, int _next) {
u = _u, v = _v, w = _w, next = _next;
}
}edge[MAXM];
初始化所有的head[i] = INF,当前边总数 edgeCount = 0
每读入一条边,调用addEdge(u, v, w),具体函数的实现如下:
void addEdge(int u, int v, int w) {
edge[ edgeCount ] = EDGE(u, v, w, head[u]);
head[u] = edgeCount ++;
}
edge[ edgeCount ] = EDGE(u, v, w, head[u]);
head[u] = edgeCount ++;
}
这个函数的含义是每加入一条边(u, v),就在原有的链表结构的首部插入这条边,使得每次插入的时间复杂度为O(1),所以链表的边的顺序和读入顺序正好是逆序的。这种结构在无论是稠密的还是稀疏的图上都有非常好的表现,空间上没有浪费,时间上也是最小开销。
调用的时候只要通过head[i]就能访问到由 i 出发的第一条边的编号,通过编号到edge数组进行索引可以得到边的具体信息,然后根据这条边的next域可以得到第二条边的编号,以此类推,直到next域为INF(这里的INF即head数组初始化的那个值,一般取-1即可)。
4、Dijkstra + 优先队列(小顶堆)
有了链式前向星,再来看Dijkstra算法,我们关注算法的第3)步,对和x直接相邻的点进行更新的时候,不再需要遍历所有的点,而是只更新和x直接相邻的点,这样总的更新次数就和顶点数n无关了,总更新次数就是总边数m,算法的复杂度变成了O(n^2 + m),之前的复杂度是O(n^2),但是有两个n^2的操作,而这里是一个,原因在于找d值最小的顶点的时候还是一个O(n)的轮询,总共n次查找。那么查找d值最小有什么好办法呢?
数据结构中有一种树,它能够在O( log(n) )的时间内插入和删除数据,并且在O(1)的时间内得到当前数据的最小值,这个和我们的需求不谋而合,它就是最小二叉堆(小顶堆),具体实现不讲了,比较简单,可以自行百度。
在C++中,可以利用STL的优先队列( priority_queue )来实现获取最小值的操作,这里直接给出利用优先队列优化的Dijkstra算法的类C++伪代码(请勿直接复制粘贴到C++编译器中编译执行),然后再进行讨论:
void Dijkstra_Heap(s) {
for(i = 0; i < n; i++) {
d[i] = (i == s) ? 0 : INF; // 注释1
}
q.push( (d[s], s) ); // 注释2
while( !q.empty() ) {
(dist, u) = q.top(); // 注释3
q.pop(); // 注释4
for (e = head[u]; e != INF; e = edge[e].next) {
v = edge[e].v;
w = edge[e].w;
if(d[u] + w < d[v]) {
d[v] = d[u] + w;
path[v] = u;
q.push( (d[v], v) );
}
}
}
}
for(i = 0; i < n; i++) {
d[i] = (i == s) ? 0 : INF; // 注释1
}
q.push( (d[s], s) ); // 注释2
while( !q.empty() ) {
(dist, u) = q.top(); // 注释3
q.pop(); // 注释4
for (e = head[u]; e != INF; e = edge[e].next) {
v = edge[e].v;
w = edge[e].w;
if(d[u] + w < d[v]) {
d[v] = d[u] + w;
path[v] = u;
q.push( (d[v], v) );
}
}
}
}
注释1:初始化s到i的初始最短距离,d[s] = 0
注释2:q即优先队列,这里略去声明是为了将代码简化,让读者能够关注算法本身而不是关注具体实现, push是执行优先队列的插入操作,插入的数据为一个二元组(d[u], u)
注释3:执行优先队列的获取操作,获取的二元组为当前队列中d值最小的
注释4:执行优先队列的删除操作,删除队列顶部的元素(即注释3中d值最小的那个二元组)
以上伪代码中的主体部分竟然没有任何注释,这是因为我要用黑色的字来描述它的重要性,而注释只是注释一些和语法相关的内容。
主体代码只有一个循环,这个循环就是遍历了u这个结点的边链表,其中e为边编号,edge[e].w即上文提到的w(u, v),即u ->v 这条边的权值,而d[u] + w(u, v) < d[v]表示从起点s到u,再经过(u, v)这条边到达v的最短路比之前其它方式到达v的最短路还短,如图二-4-1所示,如果满足这个条件,那么就更新这条最短路,并且利用path数组来记录最短路中每个结点的前驱结点,path[v] = u,表示到达v的最短路的前驱结点为u。

图二-4-1
补充一点,这个算法求出的是一棵最短路径树,其中s为根结点,结点之间的关系是通过path数组来建立的,path[v] = u,表明u为v的父结点(树的存储不一定要存儿子结点,也可以用存父结点的方式表示)。
考虑这个算法的复杂度,如果用n表示点数,m表示边数,那么优先队列中最多可能存在的点数有多少?因为我们在把顶点插入队列的时候并没有判断队列中有没有这个点,而且也不能进行这样的判断,因为新插入的点一定会取代之前的点(距离更短才会执行插入),所以同一时间队列中的点有可能重复,插入操作的上限是m次,所以最多有m个点,那么一次插入和删除的操作的平摊复杂度就是O(logm),但是每次取距离最小的点,对于有多个相同点的情况,如果那个点已经出过一次队列了,下次同一个点出队列的时候它对应的距离一定比之前的大,不需要用它去更新其它点,因为一定不可能更新成功,所以真正执行更新操作的点的个数其实只有n个,所以总体下来的平均复杂度为O( (m+n)log m),而这个只是理论上界,一般问题中都是很快就能找到最短路的,所以实际复杂度会比这个小很多,相比O(n^2)的算法已经优化了很多了。
Dijkstra算法求的是正权图的单源最短路问题,对于权值有负数的情况就不能用Dijkstra求解了,因为如果图中存在负环,Dijkstra带优先队列优化的算法就会进入一个死循环,因为可以从起点走到负环处一直将权值变小 。对于带负权的图的最短路问题就需要用到Bellman-Ford算法了。
5、Bellman-Ford
Bellman-Ford算法可以在最短路存在的情况下求出最短路,并且在存在负权圈的情况下告诉你最短路不存在,前提是起点能够到达这个负权圈,因为即使图中有负权圈,但是起点到不了负权圈,最短路还是有可能存在的。它是基于这样一个事实:一个图的最短路如果存在,那么最短路中必定不存在圈,所以最短路的顶点数除了起点外最多只有n-1个。
Bellman-Ford同样也是利用了最短路的最优子结构性质,用d[i]表示起点s到i的最短路,那么边数上限为 j 的最短路可以通过边数上限为 j-1 的最短路 加入一条边 得到,通过n-1次迭代,最后求得s到所有点的最短路。
具体算法描述如下:对于图G = <V, E>,源点为s,d[i]表示s到i的最短路。
1) 初始化 所有顶点 d[i] = INF, 令d[s] = 0,计数器 j = 0;
2) 枚举每条边(u, v),如果d[u]不等于INF并且 d[u] + w(u, v) < d[v],则令d[v] = d[u] + w(u, v);
3) 计数器j + +,当j = n - 1时算法结束,否则继续重复2)的步骤;
第2)步的一次更新称为边的“松弛”操作。
以上算法并没有考虑到负权圈的问题,如果存在负圈权,那么第2)步操作的更新会永无止境,所以判定负权圈的算法也就出来了,只需要在第n次继续进行第2)步的松弛操作,如果有至少一条边能够被更新,那么必定存在负权圈。
这个算法的时间复杂度为O(nm),n为点数,m为边数。
这里有一个小优化,我们可以注意到第2)步操作,每次迭代第2)步操作都是做同一件事情,也就是说如果第k(k <= n-1)次迭代的时候没有任何的最短路发生更新,即所有的d[i]值都未发生变化,那么第k+1次必定也不会发生变化了,也就是说这个算法提前结束了。所以可以在第2)操作开始的时候记录一个标志,标志初始为false,如果有一条边发生了松弛,那么标志置为true,所有边枚举完毕如果标志还是false则提前结束算法。
这个优化在一般情况下很有效,因为往往最短路在前几次迭代就已经找到最优解了,但是也不排除上文提到的负权圈的情况,会一直更新,使得整个算法的时间复杂度达到上限O(nm),那么如何改善这个算法的效率呢?接下来介绍改进版的Bellman-Ford 一一 SPFA。
6、SPFA
SPFA( Shortest Path Faster Algorithm )是基于Bellman-Ford的思想,采用先进先出(FIFO)队列进行优化的一个计算单源最短路的快速算法。
类似Bellman-Ford的做法,我们用数组d记录每个结点的最短路径估计值,并用链式前向星来存储图G。利用一个先进先出的队列用来保存待松弛的结点,每次取出队首结点u,并且枚举从u出发的所有边(u, v),如果d[u] + w(u, v) < d[v],则更新d[v] = d[u] + w(u, v),然后判断v点在不在队列中,如果不在就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
&
以上是关于转载夜深人静写算法——差分约束的主要内容,如果未能解决你的问题,请参考以下文章