2017多校Round2(hdu6045~hdu6055)

Posted 2020-10-01 人活着就是为了Chelly

补题进度：10/11

1001（不等式）

根据题意列不等式，解一解就行了

1002（套路）

题意：

给定一个随机产生的1e6*1e6的矩阵和一个1e3*1e3的矩阵，你要回答这个1e3*1e3的小矩阵出现在大矩阵的哪个位置

分析：

每隔1e3行 1e3列去建立一个check矩阵，看看这个check矩阵在不在1e3*1e3的矩阵中（Hash就行）

那么时间复杂度就是O(1e3*1e3*hash)

一个比较好的取法是取一个1*64的矩阵，用unsigned long long把64个压成一位放入hash中

1003（贪心）

样例有误导性，贪心着来就行了，用单调队列维护

1004（找规律+逆序对）

题意：

按照其规则将数字填到一个矩阵中，问能不能通过移动空格使得最后的有序

分析：

若空格左右移动，相当于没有改变排列，逆序对奇偶性不改变

若空格上下移动，那么相当于左右移动了m-1次，因为最后空格又回到了右下角，所以上下移动一定进行偶数次，所以逆序对奇偶性也不该边

我们想要的结果逆序对是偶数，可以猜想如果原序列逆序对个数是偶数那么就可行，否则不可行（官方题解给出了这里的证明）

然后问题就是如何快速求出逆序对了

我们可以按照取数顺序考虑有多少个小于它的数放到了它后面

以第一次(1->p+1->2p+1->...)为例，我们发现对答案的贡献分别是p-1+2*(p-1)+3*(p-1)+..... 这明显可以等差数列求

然后去掉这些之后，我们发现剩余的还是单增的，算法仍旧相同

1005（DP）

题意：

给出一个n的排列(n<=3000),现在可以把连续的一段当作一组，组内进行排序，然后你可以任选两个区间进行交换，问交换后如果能变成12345...n的话，最多能分成多少块

分析：

首先一个n^3的算法很好得到

首先预处理出ma[i][j]和mi[i][j]

我们去枚举需要交换哪两个区间[a,b] [c,d]，那么很明显d=ma[a,b]，所以只需要去枚举a,b,c，而实际上符合条件的很少，所以这里枚举加些剪枝是可以看作n^2的

很明显我们需要知道f[i][j]表示区间[i,j]变为有序最多能分成多少块

那么求f是n^3的

现在我们要将求f[i][j]变成n^2的

我们发现这个dp中的k取值很有讲究，是决策单调的，并且k不能很大，如果很大就可能导致分割的两个区间不合法

我们用la[i]表示当前以i为左端点的最长可行区间是[i,la[i]]，那么f[i][j]=f[i][la[i]]+f[la[i]+1][j]

不过要注意分成的两个区间一定要是左边的左边的最大值小于等于右边的最小值，否则f[i][j]=1

这样我们利用了决策单调性将复杂度降到O(n^2)的了

1006（找规律）

题意：

分析：

刚开始想去找第一层每个数对答案的贡献，但数字量太多了，并没用

可以用特征根求出第一行的通式，然后等比求和求出第一行的S的通式

通过S的通式可以写出第二行的通式，然后再等比求和求出第二行的S的通式

再往下写两行，就能找出Fm,1的规律了

1007（原根）

队友太强辣，把切掉了，我就不补了

1008（单调栈）

题意：

对于一个n*m的方格，每个格子中都包含一种颜色，求出任意一个矩形包含颜色种数的期望。(n,m<=100)

分析：

我们单独去考虑每个位置对答案的贡献

很明显，不同的颜色互不影响，我们可以把相同的颜色挑出来单独计算

容易想到去计算这个东西的反面，当前答案=总的矩阵数-没有被任何一个点覆盖的矩形个数，但这个并不好求，所以这种求反面的想法不可行

我们定义一个位置(i,j)的有效管理矩形是以(i,j)为最左上角的矩形，那么答案就是所有位置的有效管理矩形数的和

那么我们对每一个位置去求有效管理矩形数

显然枚举上界，下界就是n，左界和右界也要枚举（注意左界右界是单调的）

那么当然没必要将每种颜色分开做，直接去枚举每个位置就行了，这样复杂度大概是O(n^4)，数据比较水直接就能过了

其实枚举左界和右界可以用单调栈进行优化

我们可以按行进行枚举，记pre[color][j]表示到当前行为止，对于第j列来说，行坐标的最大的颜色为color的格子是什么

那么我们枚举每一个j的时候，就可以把这些pre的高度放进一个单调栈中去计算就行了

这样的复杂度O(n^3)

1009（莫比乌斯反演）

题意：

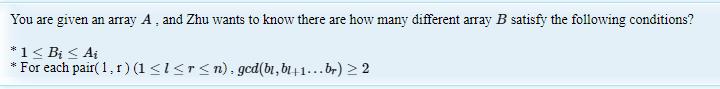
n,Ai<=10^5

分析：

对于一个B，我们去求所有数的gcd，如果这个gcd>=2，那么B是合法的，如果这个gcd=1，那么B是不合法的

gcd=1的B数量 + gcd=2的B的数量 + gcd=3的B的数量 + ...  + gcd=min(Ai)的B的数量  ==== 所有B的总数(πAi)

那么我们要求的答案就是$ans=\\prod {A_i} - (gcd=1的b的数量)$

那么莫比乌斯反演一下$ans=\\sum \\mu(d)*sum(d)$

sum(d)表示公约数为d的时候方案数，很明显$sum(d)=\\prod \\frac{A_i}{d}$

这里也要优化，将$\\frac{A_i} {d}$相同的放在一块，这里可以用一个桶来存

1010

待填坑

1011（Trick）

题目：

给了n个整点(n<=500)，问有多少个正多边形

分析：

找找规律会发现，只有正方形是可行的

所以可以枚举两个点作为正方形的相邻点，根据两个点去旋转90°以及去做一个平移操作可以得到另外两个点，判断那两个整点是否被读入覆盖就行了

时间复杂度O(n^2)