Backpropagation 算法的推导与直观图解

Posted 2020-10-01 文之

摘要

本文是对 Andrew Ng 在 Coursera 上的机器学习课程中 Backpropagation Algorithm 一小节的延伸。文章分三个部分：第一部分给出一个简单的神经网络模型和 Backpropagation（以下简称 BP）算法的具体流程。第二部分以分别计算第一层和第二层中的第一个参数（parameters，在神经网络中也称之为 weights）的梯度为例来解释 BP 算法流程，并给出了具体的推导过程。第三个部分采用了更加直观的图例来解释 BP 算法的工作流程。

注：1. 文中有大量公式，在 PC 或大屏移动设备下阅读排版更佳

　　2. 为了方便讨论，省去了 Bias unit，并在第二部分的讨论中省去了 cost function 的正则化项

　　3. 如果熟悉 Ng 课程中使用的字符标记，则推荐的阅读顺序为：第一、第三、第二部分

 

第一部分 BP 算法的具体过程

图 1.1 给出了一个简单的神经网络模型（省去了 Bias unit）：

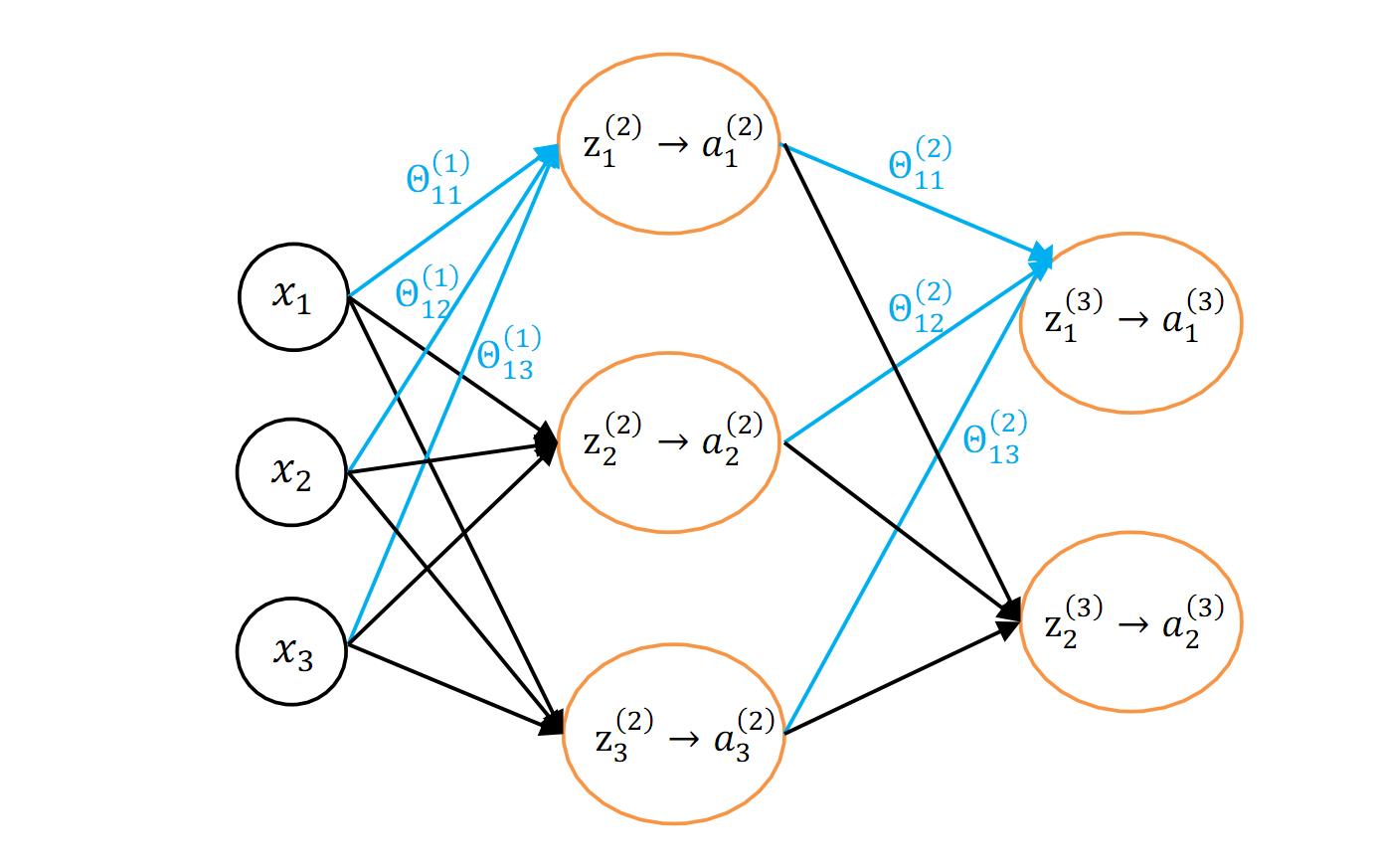
图 1.1 一个简单的神经网络模型

 

其中字符标记含义与 Ng 课程中的一致：

\\(x_1, x_2, x_3 \\) 为输入值，也即 \\(x^{(i)}\\) 的三个特征；

 \\(z^{(l)}_{j}\\) 为第 l 层的第 j 个单元的输入值。

 \\(a^{(l)}_{j}\\) 为第 l 层的第 j 个单元的输出值。其中 a = g(z)，g 为 sigmoid 函数。

 \\(\\Theta_{ij}^{(l)}\\) 第 l 层到 l+1 层的参数（权重）矩阵。

 

表 1.1 BP 算法的具体流程（Matlab 伪代码）

1    for i = m,

2        \\(a^{(1)} = x ^{(i)};\\)

3        使用前馈传播算法计算 \\(a^{(2)}, a^{(3)};\\)

4        \\(\\delta^{(3)} = a^{(3)} - y^{(i)};\\)                                                                

5        \\(\\delta^{(2)} = (\\Theta^{(2)})^T * \\delta^{(3)} .* g\\prime(z^{(2)});\\)  % 第 2 个运算符 \' .* \' 为点乘，即按元素操作

6        \\(\\Delta^{(2)} = \\Delta^{(2)} + a^{(2)} * \\delta^{(3)};\\)

7        \\(\\Delta^{(1)} = \\Delta^{(1)} + a^{(1)} * \\delta^{(2)};\\)

8    end;

 

第二部分 BP 算法步骤的详解与推导过程

 

BP 算法的目的在于为优化函数（比如梯度下降、其它的高级优化方法）提供梯度值，即使用 BP 算法计算代价函数（cost function）对每个参数的偏导值，其数学形式为：\\(\\frac{\\partial}{\\partial{\\Theta^{(l)}_{ij}}}J(\\Theta)\\)，并最终得到的值存放在矩阵 \\(\\Delta^{(l)}\\) 中。

若神经网络有 K 个输出（K classes），那么其 J(Θ) 为：

\\[J(\\Theta) = -\\frac{1}{m}\\sum_{i=1}^m\\sum_{k=1}^K[y^{(i)}_klog(h_\\Theta(x^{(i)})_k) + (1-y_k^{(i)})log(1-h_\\Theta(x^{(i)})_k)]\\]

接下来，以计算 \\(\\Theta_{11}^{(1)}, \\Theta_{11}^{(2)}\\) 为例来给出 BP 算法的详细步骤。对于单个训练用例，其代价函数为：

\\[J(\\Theta) = -[y^{(i)}_klog(h_\\Theta(x^{(i)})_k) + (1-y_k^{(i)})log(1-h_\\Theta(x^{(i)})_k)]    （式1）\\]

其中 \\(h_\\Theta(x) = a^{(l)} = g(z^{(l)})\\), g 为 sigmoid 函数。

 

计算 \\(\\Theta_{11}^{(2)}\\) 的梯度:

\\[\\frac{\\partial J(\\Theta)}{\\partial \\Theta_{11}^{(2)}} = \\frac{\\partial J(\\Theta)}{\\partial a_1^{3}} * \\frac{\\partial a_1^{(3)}}{\\partial z_1^{(3)}} * \\frac{\\partial z_1^{(3)}}{\\partial \\Theta_{11}^{(2)}}    （式 2）\\]

先取出式 2 中等号右边前两项，并将其记为 \\(\\delta_1^{(3)}\\)：

\\[\\delta_1^{(3)} = \\frac{\\partial J(\\Theta)}{\\partial a_1^{3}} * \\frac{\\partial a_1^{(3)}}{\\partial z_1^{(3)}}    （式 3）\\]

这里给出 \\(\\delta^{(l)}\\) 的定义，即：

 \\[\\delta^{(l)} = \\frac{\\partial}{\\partial z^{(l)}}J(\\Theta)^{(i)}    （式 4）\\]

对式 3 进行详细计算，即将 \\(J(\\Theta)\\) 对 \\(z_1^{(3)}\\) 求偏导（计算过程中简记为 z）：

 \\[\\delta_1^{(3)} = \\frac{\\partial J(\\Theta)}{\\partial a_1^{(3)}} * \\frac{\\partial a_1^{(3)}}{\\partial z_1^{(3)}}\\]

\\[=-[y * \\frac{1}{g(z)}*g\\prime(z) + (1-y)*\\frac{1}{1 - g(z)}*(-g\\prime(z))]\\]

\\[=-[y*(1-g(z))+(y-1)*g(z)]\\]

\\[=g(z)-y =a^{(3)}-y\\]

其中用到了 sigmoid 函数的一个很好的性质：

\\[g\\prime(z)=g(z) * (1-g(z))    （易证）\\]

这样便得到了表 1.1 中 BP 算法的第四行过程。

接下来观察式 2 中等号右边最后一项  \\(\\frac{\\partial z_1^{(3)}}{\\partial \\Theta_{11}^{(2)}}\\)：

其中 \\(z_1^{(3)}=\\Theta_{11}^{(2)}*a_1^{(2)}+\\Theta_{12}^{(2)}*a_2^{(2)}+\\Theta_{13}^{(2)}*a_3^{(2)}\\)，则易得：

 \\[\\frac{\\partial z_1^{(3)}}{\\partial \\Theta_{11}^{(2)}}=a_1^{(2)}    （式 5）\\]

再回头观察最初的式 2，代入式 3 和式 5，即可得到：

 \\[\\frac{\\partial J(\\Theta)}{\\partial \\Theta_{11}^{(2)}} = \\delta_1^{(3)} * a_1^{(2)}\\]

这样便推导出了表 1.1 中 BP 算法的第六行过程。

至此，就完成了对 \\(\\Theta_{11}^{(2)}\\) 的计算。

 

计算 \\(\\Theta_{11}^{(1)}\\) 的梯度：

 \\[\\frac{\\partial J(\\Theta)}{\\partial \\Theta_{11}^{(1)}} = \\frac{\\partial J(\\Theta)}{\\partial a_1^{3}} * \\frac{\\partial a_1^{(3)}}{\\partial z_1^{(3)}}*\\frac{\\partial z_1^{(3)}}{\\partial a_1^{(2)}}*\\frac{\\partial a_1^{(2)}}{\\partial z_1^{(2)}}*\\frac{\\partial z_1^{(2)}}{\\partial \\Theta_{11}^{(1)}}    （式 6）\\]

类似地，根据式 4 中对 \\(\\delta^{(l)}\\) 的定义，可以把上式（即式 6）等号右边前四项记为  \\(\\delta_1^{(2)}\\) 。即：

 \\[\\delta_1^{(2)}=\\frac{\\partial J(\\Theta)}{\\partial a_1^{3}} * \\frac{\\partial a_1^{(3)}}{\\partial z_1^{(3)}}*\\frac{\\partial z_1^{(3)}}{\\partial a_1^{(2)}}*\\frac{\\partial a_1^{(2)}}{\\partial z_1^{(2)}}    （式 7）\\]

可以发现式 3 中的  \\(\\delta_1^{(3)}\\)  是这个等式右边的前两项。

 

于是  \\(\\delta^{(l)}\\)  的意义就体现出来了：它是用来保存上一次计算的部分结果。在计算  \\(\\delta^{(l-1)}\\)  时，可以使用这个部分结果继续向下逐层求偏导。这样在神经网络特别复杂、有大量计算时就可以节省大量重复的运算，从而有效地提高神经网络的学习速度。

 

继续观察式 7，其等号右边第三项易算得（已知  \\(z_1^{(3)}=\\Theta_{11}^{(2)}*a_1^{(2)}+\\Theta_{12}^{(2)}*a_2^{(2)}+\\Theta_{13}^{(2)}*a_3^{(2)}\\)）：

 \\[\\frac{\\partial z_1^{(3)}}{\\partial a_1^{(2)}} = \\Theta_{11}^{(2)}    （式 8）\\]

式 7 等号右边最后一项为：

 \\[\\frac{\\partial a_1^{(2)}}{\\partial z_1^{(2)}}=g\\prime(z_1^{(2)})   （式 9） \\]

将 \\(\\delta_1^{(3)}\\)、式 8、式 9 代入式 7，即可得到：

 \\[\\delta_1^{(2)}=\\delta_1^{(3)}*\\Theta_{11}^{(2)}*g\\prime(z_1^{(2)})    （式 10）\\]

这样便推导出了表 1.1 中 BP 算法第五行过程。

接下来继续计算式 6 中等号右边最后一项，已知  \\(z_1^{(2)}=\\Theta_{11}^{(1)}*a_1^{(1)}+\\Theta_{12}^{(1)}*a_2^{(1)}+\\Theta_{13}^{(1)}*a_3^{(1)}\\)，易得：

 \\[\\frac{\\partial z_1^{(2)}}{\\partial \\Theta_{11}^{(1)}}=a_1^{(1)}    （式 11）\\]

将式 10、式 11 代入最开始的式 6 即可得：

 \\[\\frac{\\partial J(\\Theta)}{\\partial \\Theta_{11}^{(1)}} =\\delta_1^{(2)} * a_1^{(1)}\\]

如此，即可得到表 1.1 中 BP 算法的第七行过程。

至此，就完成了对 \\(\\Theta_{11}^{(1)}\\) 的计算。

 

第三部分 BP 算法的直观图解

 

神经网络学习算法图概览

给定一个函数 f(x)，它的首要求导对象是什么？就是它的输入值，是自变量 x。那 f(g(x)) 呢？即把g(x) 当作一个整体作为它的输入值，它的自变量。那么 g(x) 这个整体就是它的首要求导对象。因此，一个函数的求导对象是它的输入值，是它的自变量。弄清楚这一点，才能在求多元函数偏导的链式法则中游刃有余。

图 3.1 自下而上，每一个框是上面一个框的输入值，也即上面一个框中函数的自变量。这张图明确了神经网络中各数据之间的关系——谁是谁的输入值，图中表现得非常清楚。上段提到一个函数的求导对象是它的输入值，那么通过图 3.1 就能非常方便地使用链式法则，也能清楚地观察到 BP 算法的流程（后面一个小节会给出一个更具体的 BP 流程图）。

对照文首给出的图 1.1 神经网络的模型图，应该很容易理解图 3.1 的含义，它大致地展现了神经网络的学习（训练）流程。前馈传播算法自下而上地向上计算，最终可以得到 \\(a^{(3)}\\)，进一步可以计算得到 \\(J(\\Theta)\\)。而 BP 算法自顶向下，层层求偏导，最终得到了每个参数的梯度值。下面一个小节将仔细介绍本文的主题，即 BP 算法的流程图解。

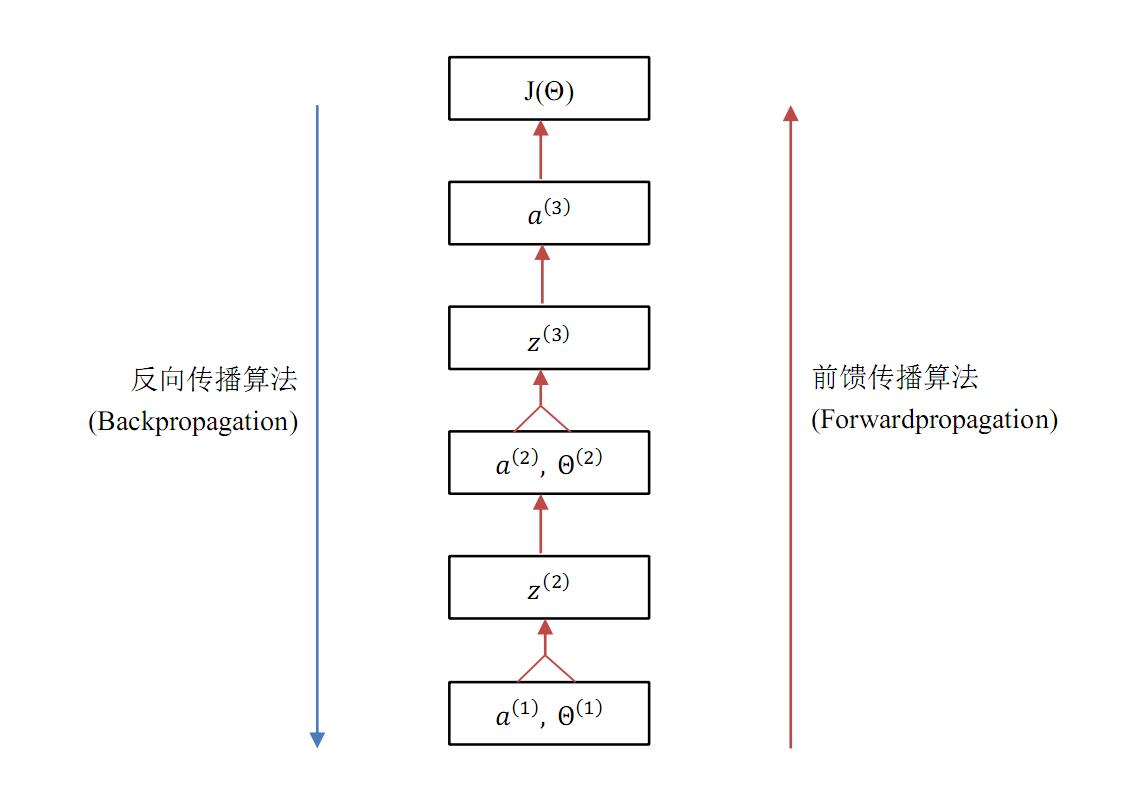
图 3.1 神经网络学习算法概览

 

BP 算法的直观图解

图 3.2 给出了 BP 算法的计算流程，并附上了具体的计算步骤。BP 算法的流程在这张图中清晰可见：自顶向下（对应神经网络模型为自输出层向输入层）层层求偏导。因为神经网络的复杂性，人们总是深陷于求多元函数偏导的泥潭中无法自拔：到底该对哪个变量求导？图 3.2 理顺了神经网络中各数据点之间的关系，谁是谁的输入值，谁是谁的函数一清二楚，然后就可以畅快地使用链式法则了。

> 如果看不清图片上的文字，可在图片上右键，选择在新窗口中打开以查看原图

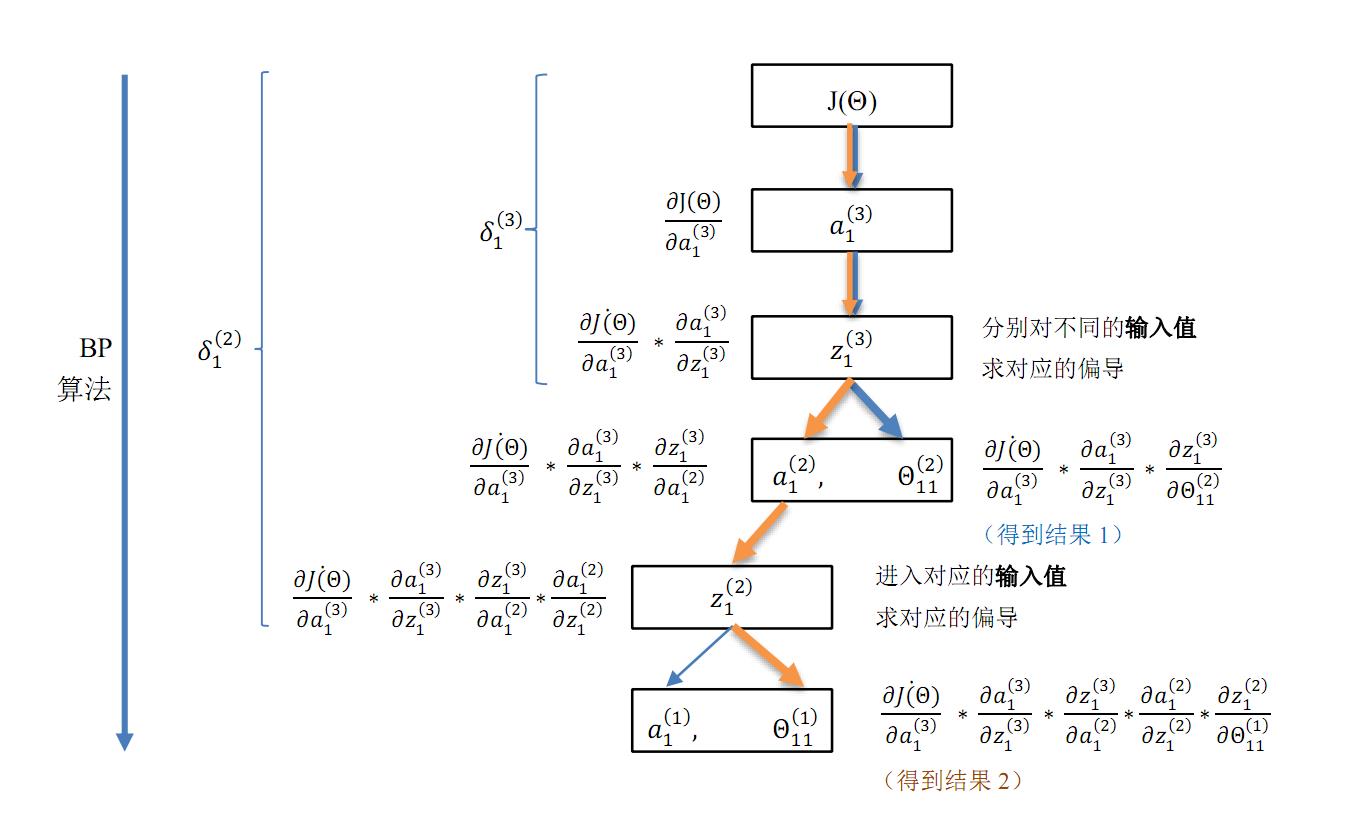
图3.2 BP 算法流程

 

所以 BP 算法即反向传播算法，就是自顶向下求代价函数 \\(J(\\Theta)\\) 对各个参数 \\(\\Theta_{ij}^{(l)}\\) 偏导的过程，对应到神经网络模型中即自输出层向输入层层层求偏导。在图 3.2 中，当反向传播到 \\(a_1^{(2)}\\) 结点时，遇到分叉路口：选择对 \\(\\Theta_{11}^{(2)}\\) 求偏导，即可得到第二层的参数梯度。而若选择对 \\(a_1^{(2)}\\) 这条路径继续向下求偏导，就可以继续向下（即输出层）传播，继续向下求偏导，最终可得到第一层的参数梯度，于是就实现了 BP 算法的目的。在选择分叉路口之前，使用 \\(\\delta^{(l)}\\) 来保存到达分岔路口时的部分结果（本文的第二部分对 \\(\\delta^{(l)}\\) 做出了精确定义）。那么如果选择继续向下求偏导，则还可以使用这个部分结果继续向下逐层求偏导。从而避免了大量的重复计算，有效地提升了神经网络算法的学习速度。

 

因此可以观察到 BP 算法两个突出特点：

1) 自输出层向输入层（即反向传播），逐层求偏导，在这个过程中逐渐得到各个层的参数梯度。

2) 在反向传播过程中，使用 \\(\\delta^{(l)}\\) 保存了部分结果，从而避免了大量的重复运算。

 

（完）