数据结构基础_图
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构基础_图相关的知识,希望对你有一定的参考价值。
图
黑白图像
题目:输入一个n*n的黑白图像(1表示黑色,0表示白色),任务是统计其中的八连块的个数。如果两个黑格子有公共边或者公共顶点,就说它们属于同一个八连块。
输入:
6
100100
001010
000000
110000
111000
010100
输出:
3
1 #include <stdio.h> 2 #include<string.h> 3 const int MAXN=100; 4 int mat[MAXN][MAXN],vis[MAXN][MAXN]; 5 char s[MAXN*MAXN]; 6 void dfs(int x,int y){ 7 if(!mat[x][y]||vis[x][y]) return;//曾经访问过这个各自,或者当前格子是白色 8 vis[x][y]=1; 9 dfs(x-1,y-1);dfs(x-1,y);dfs(x-1,y+1); 10 dfs(x,y-1); dfs(x,y+1); 11 dfs(x+1,y-1);dfs(x+1,y);dfs(x+1,y+1); 12 } 13 14 int main() { 15 memset(mat,0,sizeof(mat)); 16 memset(vis,0,sizeof(vis)); 17 int n; 18 scanf("%d",&n); 19 for(int i=0;i<n;i++){ 20 scanf("%s",s); 21 for(int j=0;j<n;j++){ 22 mat[i+1][j+1]=s[j]-‘0‘;//把图像往中间移动一点,空出一圈白格子 23 } 24 } 25 int count=0; 26 for(int i=1;i<=n;i++){ 27 for(int j=1;j<=n;j++){ 28 if(!vis[i][j]&&mat[i][j]){ 29 count++; 30 dfs(i,j); 31 } 32 } 33 } 34 printf("%d\\n",count); 35 return 0; 36 }
走迷宫(借鉴加篡改  )
)
题目:一个网络迷宫由n行m的单元格组成,每个单元格要么是空地(1),要么是障碍物(0)。你的任务是照一天从起点到重点的最短移动序列,其中UDLR表示往上下左右移动单元格
输出:
(2,1) 1 D
(3,1) 1 D
(4,1) 1 D
(5,1) 1 D
(5,2) 3 R
(5,3) 3 R
(4,3) 0 U
(3,3) 0 U
(2,3) 0 U
(2,4) 3 R
(1,4) 0 U
(1,5) 3 R
二叉树的BFS是结点的访问顺序恰好是它们到根结点距离从小到大的顺序。类似地,也可以用BFS来按照到起点的距离顺序遍历迷宫图。
1 #include<stdio.h> 2 const int row=8; 3 const int col=7; 4 5 int maze[row][col]={ 6 {0,0,0,0,0,0,0}, 7 {0,1,1,0,1,1,0}, 8 {0,1,0,1,1,1,0}, 9 {0,1,0,1,0,0,0}, 10 {0,1,0,1,1,1,0}, 11 {0,1,1,1,0,1,0}, 12 {0,1,1,1,1,1,0}, 13 {0,0,0,0,0,0,0} 14 }; 15 16 int fa[row][col]; //记录位置(x,y)的上一步 17 int last_dir[row][col];//记录上一步到达(x,y)的方向(上下左右) 18 int dist[row][col];//(x,y)距离起点的距离 19 int vis[row][col];//访问标记 20 21 char load[4]={‘U‘,‘D‘,‘L‘,‘R‘};//广度优先的遍历顺序 22 int dx[4]={-1,1,0,0};//上下左右移动时,x的变化步伐 23 int dy[4]={0,0,-1,1};//上下左右移动时,y的变化步伐 24 25 26 int queue[row*col]; 27 void BFS(int x,int y) 28 {//广度优先遍历结点,其中参数x,y代表迷宫的出发点。 29 //本方法旨在求出从x,y出发到各点的最短路径 30 int u=col*x+y; 31 fa[x][y]=u;//出发点的父结点就是其本身,以此作为起点的标志,在遍历的时候需要用到 32 dist[x][y]=0; 33 vis[x][y]=1; 34 int front=0,rear=0; 35 queue[rear++]=u; 36 while(front<rear){ 37 u=queue[front++]; 38 int x=u/col; 39 int y=u%col; 40 for(int i=0;i<4;++i){//遍历四个方向 41 int nx=x+dx[i]; 42 int ny=y+dy[i]; 43 if( maze[nx][ny] && !vis[nx][ny]){ 44 int v=nx*col+ny; 45 queue[rear++]=v; 46 vis[nx][ny]=1; 47 fa[nx][ny]=u; 48 dist[nx][ny]=dist[x][y]+1; 49 last_dir[nx][ny]=i; 50 } 51 } 52 } 53 } 54 55 void print_load(int x,int y) 56 {//打印指定终点(x,y)的最短路径 57 int u=fa[x][y]; 58 if(u!=(x*col+y)){//在DFS(x,y)方法中约定的当fa[x][y]=col*x+y时表示该结点为起点 59 int nx=u/col; 60 int ny=u%col; 61 print_load(nx,ny); 62 printf("(%d,%d) %d %c\\n",x,y,last_dir[x][y],load[last_dir[x][y]]); 63 } 64 } 65 66 int main() 67 { 68 BFS(1,1); 69 print_load(1,5); 70 return 0; 71 }
拓扑排序
题目:假设有n个变量,还有m个二元组(u,v),分别表示变量u小于v。那么,所有变量从小到大排列起来应该是什么样子的呢?例如有4个变量a,b,c,d,若已知a<b,c<b,d<c,则这4个变量的排序可能是a<d<c<b。尽管还有其他可能(如d<a<c<b),你只需找出其中一个即可。
输出:
b a g c d e f
 (别人家的图)
(别人家的图)
1 #include <stdio.h> 2 #include<string.h> 3 #include <string.h> 4 const int max=7; 5 int maze[max][max]={ 6 {0,0,1,0,0,0,1}, 7 {0,0,1,1,0,0,0}, 8 {0,0,0,1,0,1,0}, 9 {0,0,0,0,1,0,0}, 10 {0,0,0,0,0,1,0}, 11 {0,0,0,0,0,0,0}, 12 {0,0,1,0,0,0,0} 13 }; 14 15 char node[max]={‘a‘,‘b‘,‘c‘,‘d‘,‘e‘,‘f‘,‘g‘}; 16 17 18 /* 19 int maze[max][max]={ 20 {0,1,0,1,0,0,0}, 21 {0,0,1,0,0,0,0}, 22 {0,0,0,0,1,0,0}, 23 {0,1,0,0,1,0,0}, 24 {0,0,0,0,0,0,0}, 25 {0,0,0,1,0,0,1}, 26 {0,0,0,1,0,0,0} 27 }; 28 char node[max]={‘b‘,‘d‘,‘e‘,‘c‘,‘f‘,‘a‘,‘g‘}; 29 */ 30 31 int vis[max]; 32 int topo[max],cur; 33 34 bool DFS(int u) 35 {//深度优先遍历,抽取从u出发的路径,并保存在topo(相当于栈)中 36 vis[u]=-1; 37 for(int v=0;v<max;++v){//遍历与u相连的所有的点 38 if(maze[u][v]){ 39 if(vis[v]<0) return false; 40 else if(!vis[v] && !DFS(v)) return false; 41 } 42 } 43 vis[u]=1; 44 topo[--cur]=u; 45 return true; 46 } 47 48 bool topo_sort() 49 { 50 cur=max;//假设栈底位于此,栈最顶端为0 51 memset(topo,0,sizeof(topo)); 52 memset(vis,0,sizeof(vis)); 53 for(int u=0;u<max;++u){ 54 if(!vis[u] && !DFS(u)) return false; 55 } 56 return true; 57 } 58 59 void print_topo() 60 {//输出拓扑排序 61 int flag=0; 62 for(int v=0;v<max;v++){ 63 printf(flag++? " %c":"%c",node[topo[v]]); 64 } 65 } 66 67 int main() 68 { 69 if(topo_sort()){ 70 print_topo(); 71 printf("\\n"); 72 } 73 return 0; 74 }
进入难关,渐渐力不从心。什么鬼,dfs和bfs说是就是,到底有什么界限,说深度和宽度,画图倒是挺简单,难的使用代码表示出来。嗯,要好好研究一下。
首先是bfs(宽度),按层次顺序去遍历一棵树,主要使用队列来实现,做完这个节点相关联的所有节点,在跑去做下一个节点。
其次是dfs(深度),访问一个节点过后,要访问这个节点相关联的所有节点的其中一个节点,然后重复往下走。
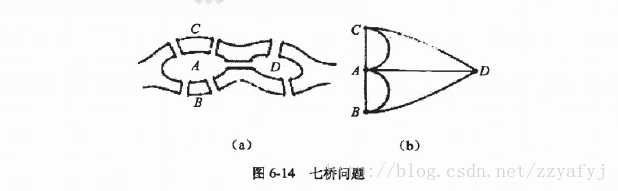
欧拉回路
题目:有一条命为Pregel的河流经过Konigsberg。城中有七座桥,把河中的两个岛与河岸连接起来。是否存在一条路线,可以不重复地走完7座桥 。
欧拉道路实际上是一笔画问题:欧拉图必须满足条件:图连通并且没有度数为奇数的节点
半连通(半连通的定义,有向图G(V,E),任意两个不同的点u、v,u有一条路径可达v或者v有一条路径可达u)
+
恰有2个度数为奇数的节点(这两个顶点为初始和结束顶点,因为其他节点进出次数相等)
如何判定恰有两个度数为奇数的节点:枚举即可 。
输出:
Euler path...
c d a c b a
1 #include<stdio.h> 2 #include <string.h> 3 #define max 4 4 //存在欧拉路径 5 int G[4][4]={ 6 {0,1,1,1}, 7 {1,0,1,0}, 8 {1,1,0,1}, 9 {1,0,1,0} 10 }; 11 /* 12 //存在欧拉回路 13 int G[4][4]={ 14 {0,1,0,1}, 15 {1,0,1,0}, 16 {0,1,0,1}, 17 {1,0,1,0} 18 }; 19 */ 20 char city[max]={‘a‘,‘b‘,‘c‘,‘d‘}; 21 int degree[max]; 22 void cal_degree() 23 {//计算所有结点的度 24 int pos=0; 25 for(int i=0;i<max;i++){ 26 for(int j=0;j<max;j++){ 27 if(G[i][j]) degree[i]++; 28 } 29 } 30 } 31 int stack[max*max]={0},top=0; 32 int visited[max][max]={0}; 33 void print_load() 34 {//输出欧拉回路,并将栈顶置零 35 int flag=0; 36 if(top>0){ 37 while(top>0){ 38 printf(flag++? " %c":"%c",city[stack[--top]]);} 39 top=0;printf("\\n"); 40 } 41 } 42 43 void DFS(int u) 44 { //深度优先遍历图,找出路径 45 stack[top++]=u; 46 for(int v=0;v<max;v++){ 47 if(G[u][v] && !visited[u][v]){ 48 visited[u][v]=visited[v][u]=1; 49 DFS(v); 50 print_load(); 51 } 52 } 53 } 54 55 void euler_path() 56 {//计算欧拉道路或欧拉回路 57 int start=-1; 58 for(int i=0;i<max;++i){//若存在奇点,找出第一个奇点作为起点 59 if(degree[i]%2) { 60 start=i; 61 break; 62 } 63 } 64 if(start<0) start=0;//不存在奇点,把第一个点作为起点 65 DFS(start); 66 } 67 68 int cal_odd_node() 69 {//统计奇点的个数 70 int odd_node=0; 71 for(int i=0;i<max;i++){ 72 if(degree[i]%2) odd_node++; 73 } 74 return odd_node; 75 } 76 77 int main() 78 { 79 memset(degree,0,sizeof(degree)); 80 cal_degree(); 81 int odd_node=cal_odd_node(); 82 if(odd_node==2 || odd_node==0){//存在欧拉路径的充分条件 83 printf("Euler path...\\n"); 84 if(odd_node==0){//存在欧拉回路的充分条件 85 printf("Euler circuit...\\n"); 86 } 87 euler_path(); 88 }else{//不存在欧拉道路或回路 89 printf("no...\\n"); 90 } 91 return 0; 92 }
以上是关于数据结构基础_图的主要内容,如果未能解决你的问题,请参考以下文章