线段树 区间乘

Posted 2020-10-01 wang者归来

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.将某区间每一个数乘上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

 

输出格式：

 

输出包含若干行整数，即为所有操作3的结果。

 

输入输出样例

输入样例#1：

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1：

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

 

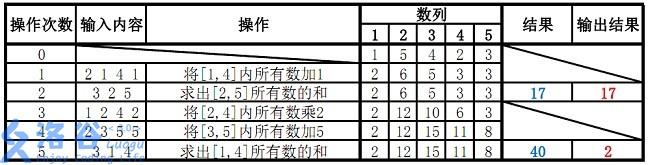
一个小错误改了一上午

#include<iostream>
#include<queue>
#include<cstdio>
#include<math.h>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
long long n,Q;
long long ans,P;
long long sum[400009];
long long dx[400009],ch[400009];
long long a[400009];
void build(LL l,LL r,LL  id)
{    ch[id]=1;sum[id]=0;
    if(l==r)    {sum[id]=a[l]%P;return;}
    int mid=(l+r)/2;
    build(l,mid,id*2);build(mid+1,r,id*2+1);
    sum[id]= (sum[id*2] + sum[id*2+1])%P;    
    return;
}
void cheng(LL l,LL r,LL id,LL tl,LL tr,LL x)
{
    if(tl<=l&&r<=tr)    
    {
        ch[id]=((LL)ch[id]*x)%P;
        dx[id]=((LL)dx[id]*x)%P;
        sum[id]=((LL)sum[id]*x)%P;
        return;
    }
    int mid=(l+r)/2;
    if((ch[id]!=1) || dx[id])
    {
        dx[id<<1]=((LL)dx[id<<1]*ch[id]+dx[id])%P;
        ch[id<<1]=((LL)ch[id<<1]*ch[id])%P;
        sum[id<<1]=(((LL)sum[id<<1]*ch[id])%P+(LL)dx[id]*(mid-l+1)%P)%P;
    
        ch[id<<1|1]=((LL)ch[id<<1|1]*ch[id])%P;dx[id<<1|1]=((LL)dx[id<<1|1]*ch[id]+dx[id])%P;
        sum[id<<1|1]=(((LL)sum[id<<1|1]*ch[id])%P+(LL)dx[id]*(r-mid)%P)%P;
    
        ch[id]=1;dx[id]=0;
    }
    
    if(tl<=mid)    cheng(l,mid,id*2,tl,tr,x);    
    if(tr>=mid+1) cheng(mid+1,r,id*2+1,tl,tr,x);
    sum[id]=(sum[id<<1]+sum[id<<1|1])%P;        
    return ;
}
void add(LL l,LL r,LL id,LL tl,LL tr,LL x)
{
    if(tl<=l&&r<=tr)    
    {
        (dx[id]+=x)%P;
        (sum[id]+=(LL)(r-l+1)*x)%P;
        return;
    }
    int mid=(l+r)/2;        
    if( dx[id] || ( ch[id]!=1 ))
    {
        ch[id<<1]=((LL)ch[id<<1]*ch[id])%P;dx[id<<1]=((LL)dx[id<<1]*ch[id]+dx[id])%P;
        sum[id<<1]=(((LL)sum[id<<1]*ch[id])%P+(LL)dx[id]*(mid-l+1)%P)%P;
    
        ch[id<<1|1]=((LL)ch[id<<1|1]*ch[id])%P;dx[id<<1|1]=((LL)dx[id<<1|1]*ch[id]+dx[id])%P;
        sum[id<<1|1]=(((LL)sum[id<<1|1]*ch[id])%P+(LL)dx[id]*(r-mid)%P)%P;
    
        ch[id]=1;dx[id]=0;
    }
    if(tl<=mid) add(l,mid,id*2,tl,tr,x);    
    if(tr>=mid+1) add(mid+1,r,id*2+1,tl,tr,x);
    sum[id]=(sum[id<<1]+sum[id<<1|1])%P;
    return ;
}
long long ask(LL l,LL r,LL id,LL tl,LL tr)
{
    if(tl<=l&&r<=tr)    
        return sum[id]%P;        
    int mid=(l+r)/2;
    if( dx[id] || ( ch[id]!=1 ))
    {
        ch[id<<1]=((LL)ch[id<<1]*ch[id])%P;dx[id<<1]=((LL)dx[id<<1]*ch[id]+dx[id])%P;
        sum[id<<1]=(((LL)sum[id<<1]*ch[id])%P+(LL)dx[id]*(mid-l+1)%P)%P;
    
        ch[id<<1|1]=((LL)ch[id<<1|1]*ch[id])%P;dx[id<<1|1]=((LL)dx[id<<1|1]*ch[id]+dx[id])%P;
        sum[id<<1|1]=(((LL)sum[id<<1|1]*ch[id])%P+(LL)dx[id]*(r-mid)%P)%P;
    
        ch[id]=1;dx[id]=0;
    }
    long long ans=0;
    if(tl <= mid)        
        ans=(ans+ask(l,mid,id*2,tl,tr))%P;
    if(tr >= mid+1)
        ans=(ans+ask(mid+1,r,id*2+1,tl,tr))%P;    
    return ans%P;
}
int main()
{
    scanf("%lld%lld%lld",&n,&Q,&P);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    build(1,n,1);
    
    for(LL i=1,A,l,r,x;i<=Q;i++)
    {
        scanf("%lld",&A);
        if(A==1)
        {
            scanf("%lld%lld%lld",&l,&r,&x);
            cheng(1,n,1,l,r,x);            
        }else
        if(A==2)
        {
            scanf("%lld%lld%lld",&l,&r,&x);
            add(1,n,1,l,r,x);
        }else
        {
            scanf("%lld%lld",&l,&r);
            cout<<ask(1,n,1,l,r)%P<<endl;
        }
    }
    return 0;
}