[矩阵乘法][DP]Vijos1067 Warcraft III 守望者的烦恼

Posted 2020-10-01

题目梗概

n个单位的路程，主角每次最多可以走k个单位(也就是每次可以走1-k个单位)，问最后到第n个监狱的方法数。

思考

DP转移方程并不难推导:

dp[i]表示第i个监狱的方法数

$dp\\left [ i \\right ] = dp\\left [ i-1 \\right ] + dp\\left [ i-2 \\right ]\\cdots \\cdots + dp\\left [ i-k-1 \\right ]$

但是这个n有点太大了，所以我们需要对DP方程进行优化。

仔细观察转移方程会发现，每次都是加上 上一个，减去上一个的末尾。 所以这种形式我们就可以用矩阵来进行优化了。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int N = 25;
const int MOD = 7777777;
typedef long long LL;
int t,m,n,k;
struct Mat
{
LL s[12][12];
}a,b;
Mat multiply(Mat x, Mat y)
{
    Mat c;
    memset(c.s,0,sizeof(c.s));
    for(int i = 0;i < k; ++i)
        {
            for(int j = 0;j < k; ++j)
            {
                for(int z = 0; z < k; ++z)
                {
                    c.s[i][j] += x.s[i][z] * y.s[z][j];
                    c.s[i][j] %= MOD;
                }
            }
        }
    return c;
}
void init()
{
    memset(a.s,0,sizeof(a.s));
    memset(b.s,0,sizeof(b.s));
        //这里看不懂的看我下面的图片
    a.s[0][0] = 1;
    for(int i = 1; i < k; ++i)
    {
        a.s[i][i-1] = 1;
        a.s[0][i] = 1;
    }
    for(int i = 0; i < k;i++)
    b.s[i][0] = 1;
}
LL calc(){
    while(n)//矩阵快速幂
    {
        if(n & 1)
        b = multiply(b,a);
        a = multiply(a,a);
        n >>= 1;
    }
    return b.s[0][0];
}
int main()
{
    while(~scanf("%d%d",&k,&n))
    { 
    init();
    LL ans = calc();
    printf("%lld\\n",ans);
    }
}

首先看我这个Tex，我们假定k是2，建立一个2*2的矩阵,就拿样例说吧。

n=1 

n=2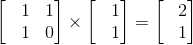 

n=3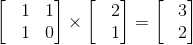 

n=4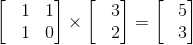 

这个2*2的矩阵是辅助作用，它有什么作用呢？首先按照矩阵乘法，产生的新矩阵的第一行储存的是当前dp[i]的值,第二行储存的是是dp[i-1]的值，用矩阵相乘的形式，来计算DP方程。但是时间复杂度O(n)，那还不是等于没优化吗？

这时候我们就可以使用矩阵快速幂(时间复杂度${log_{2}}^{n}$)，矩阵快速幂不懂的去百度教程。

再简述一下为什么矩阵快速幂是可行的:

因为矩阵乘法具有结合律 A*B*C=A*C*B

所以$A\\times B^{n} = A\\times B^{n-2}\\times B^{2}=A \\times B^{2} \\times B^{n-2}$