多项式回归学习笔记
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了多项式回归学习笔记相关的知识,希望对你有一定的参考价值。
操作系统 : CentOS7.3.1611_x64
python版本:2.7.5
sklearn版本:0.18.2
tensorflow版本 :1.2.1
多项式的定义及展现形式
多项式(Polynomial)是代数学中的基础概念,是由称为不定元的变量和称为系数的常数通过有限次加减法、乘法以及自然数幂次的乘方运算得到的代数表达式。
多项式分为一元多项式和多元多项式,其中:
不定元只有一个的多项式称为一元多项式;
不定元不止一个的多项式称为多元多项式。
本文讨论的是一元多项式相关问题。
其一般形式如下(python语法表达方式):
y = a0 + a1 * x + a2 * (x**2) + ... + an * (x ** n) + e
比如普通的二次多项式回归模型如下(python语法表达方式):
y = a0 + a1 * x + a2 * (x**2) + e
当 a0,a1,a2,e = 10,2,-0.03,0.5 时,大致图形如下:
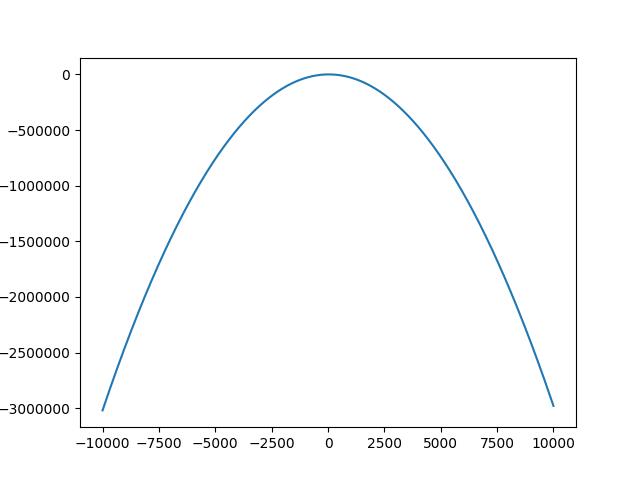
源码如下:
#! /usr/bin/env python #-*- coding:utf-8 -*- import pylab import pandas as pd def fun(x): # y = a0 + a1 * x + a2 * (x**2) + e a0,a1,a2,e = 10,2,-0.03,0.5 y = a0 + a1 * x + a2 * (x**2) + e return y arrX = range(-10000,10000) arrY = [] for x in arrX : arrY.append(fun(x)) pylab.plot(arrX,arrY) pylab.show()
普通的三次多项式回归模型如下(python语法表达方式):
y = a0 + a1 * x + a2 * (x**2) + a3 * (x**3) + e
当 a0,a1,a2,a3,e = 10,-0.2,-0.03,-0.04,0.5 时,大致图形如下:
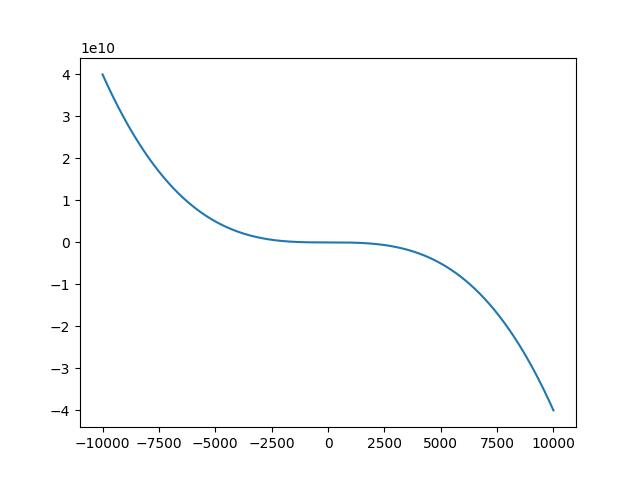
源码如下:
#! /usr/bin/env python #-*- coding:utf-8 -*- import pylab import pandas as pd def fun(x): # y = a0 + a1 * x + a2 * (x**2) + a3 * (x**3)+ e a0,a1,a2,a3,e = 10,-0.2,-0.03,-0.04,0.5 y = a0 + a1 * x + a2 * (x**2) + a3 * (x**3)+ e return y arrX = range(-10000,10000) arrY = [] for x in arrX : arrY.append(fun(x)) pylab.plot(arrX,arrY) pylab.show()
多项式回归
在单因子(连续变量)试验中,当回归函数不能用直线来描述时,要考虑用非线性回归函数。 多项式回归属于非线性回归的一种。 这里指单因子多项式回归,即一元多项式回归。
一般非线性回归函数是未知的,或即使已知也未必可以用一个简单的函数变换转化为线性模型。这时,常用的做法是用因子的多项式。 如果从散点图观察到回归函数有一个“弯”,则可考虑用二次多项式;有两个弯则考虑用三次多项式;有三个弯则考虑用四次多项式,等等。
真实的回归函数未必就是某个次数的多项式,但只要拟合得好,用适当的多项式来近似真实的回归函数是可行的。
使用sklearn解决多项式回归问题
示例代码如下:
#! /usr/bin/env python #-*- coding:utf-8 -*- # 多项式回归 import matplotlib.pyplot as plt import numpy as np from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures rng = np.random.RandomState(1) def fun(x): a0,a1,a2,a3,e = 0.1,-0.02,0.03,-0.04,0.05 y = a0 + a1 * x + a2 * (x**2) + a3 * (x**3)+ e y += 0.03 * rng.rand(1) return y plt.figure() plt.title(\'polynomial regression(sklearn)\') plt.xlabel(\'x\') plt.ylabel(\'y\') plt.grid(True) X = np.linspace(-1, 1, 30) arrY = [fun(x) for x in X] X = X.reshape(-1,1) y = np.array(arrY).reshape(-1,1) plt.plot(X, y, \'k.\') qf = PolynomialFeatures(degree=3) qModel = LinearRegression() qModel.fit(qf.fit_transform(X), y) X_predict = np.linspace(-1, 2, 100) X_predict_result = qModel.predict(qf.transform(X_predict.reshape(X_predict.shape[0], 1))) plt.plot(X_predict,X_predict_result , \'r-\') plt.show()
该代码github地址:https://github.com/mike-zhang/pyExamples/blob/master/algorithm/NonLinearRegression/pr_sklearn_test1.py
运行效果图如下:
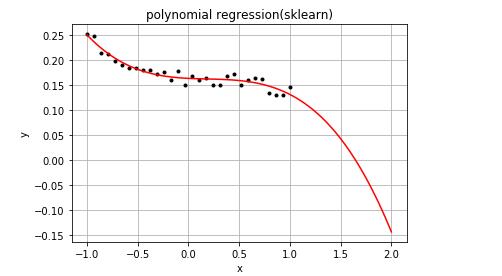
使用tensorflow解决多项式回归问题
示例代码如下:
#! /usr/bin/env python #-*- coding:utf-8 -*- import tensorflow as tf import numpy as np import matplotlib.pyplot as plt learning_rate = 0.01 training_epochs = 40 rng = np.random.RandomState(1) def fun(x): a0,a1,a2,a3,e = 0.1,-0.02,0.03,-0.04,0.05 y = a0 + a1 * x + a2 * (x**2) + a3 * (x**3)+ e y += 0.03 * rng.rand(1) return y trX = np.linspace(-1, 1, 30) arrY = [fun(x) for x in trX] num_coeffs = 4 trY = np.array(arrY).reshape(-1,1) X = tf.placeholder("float") Y = tf.placeholder("float") def model(X, w): terms = [] for i in range(num_coeffs): term = tf.multiply(w[i], tf.pow(X, i)) terms.append(term) return tf.add_n(terms) w = tf.Variable([0.] * num_coeffs, name="parameters") y_model = model(X, w) cost = tf.reduce_sum(tf.square(Y-y_model)) train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) with tf.Session() as sess : init = tf.global_variables_initializer() sess.run(init) for epoch in range(training_epochs): for (x, y) in zip(trX, trY): sess.run(train_op, feed_dict={X: x, Y: y}) w_val = sess.run(w) print(w_val) plt.figure() plt.xlabel(\'x\') plt.ylabel(\'y\') plt.grid(True) plt.title(\'polynomial regression(tensorflow)\') plt.scatter(trX, trY) trX2 = np.linspace(-1, 2, 100) trY2 = 0 for i in range(num_coeffs): trY2 += w_val[i] * np.power(trX2, i) plt.plot(trX2, trY2, \'r-\') plt.show()
该代码github地址:https://github.com/mike-zhang/pyExamples/blob/master/algorithm/NonLinearRegression/pr_tensorflow_test1.py
运行效果如下:
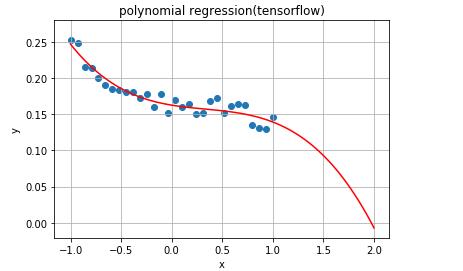
好,就这些了,希望对你有帮助。
本文github地址:
https://github.com/mike-zhang/mikeBlogEssays/blob/master/2017/20170804_多项式回归学习笔记.rst
欢迎补充
以上是关于多项式回归学习笔记的主要内容,如果未能解决你的问题,请参考以下文章