线性回归问题

Posted 2020-10-01 dear_diary

1. 简单线性回归介绍：

• 回归(regression) Y变量为连续数值型(continuous numerical variable)

                    如：房价，人数，降雨量

• 分类(Classification): Y变量为类别型(categorical variable)

                    如：颜色类别，电脑品牌，有无信誉

     

2. 简单线性回归(Simple Linear Regression)

     2.1 很多做决定过过程通常是根据两个或者多个变量之间的关系

     2.3 回归分析(regression analysis)用来建立方程模拟两个或者多个变量之间如何关联

     2.4 被预测的变量叫做：因变量(dependent variable), y, 输出(output)

     2.5 被用来进行预测的变量叫做： 自变量(independent variable), x, 输入(input)

 

3. 简单线性回归介绍

     3.1 简单线性回归包含一个自变量(x)和一个因变量(y)

     3.2 以上两个变量的关系用一条直线来模拟

     3.3 如果包含两个以上的自变量，则称作多元回归分析(multiple regression)

 

4. 简单线性回归模型

     4.1 被用来描述因变量(y)和自变量(X)以及偏差(error)之间关系的方程叫做回归模型

     4.2 简单线性回归的模型是:
　　　   　              

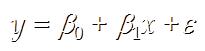
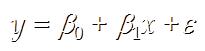
          其中：            参数         参数               偏差

 

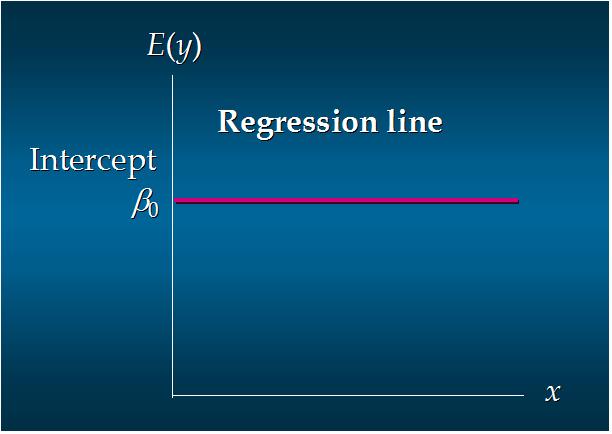
5. 简单线性回归方程

                         E(y) = β₀+β₁x 

         这个方程对应的图像是一条直线，称作回归线

         其中，β₀是回归线的截距

                  β₁是回归线的斜率  

                  E(y)是在一个给定x值下y的期望值（均值）

 

6. 正向线性关系：

               

 

 

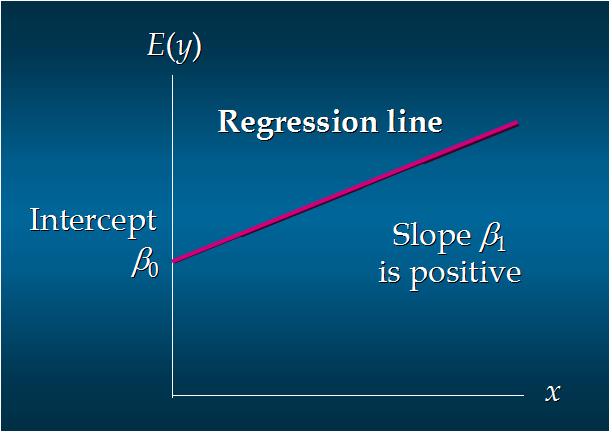
7. 负向线性关系：

 

 

 

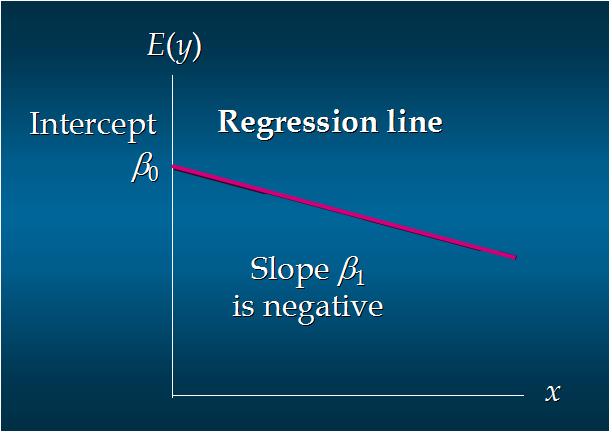
  8. 无关系

 

 

 

9. 估计的简单线性回归方程

          ŷ=b₀+b₁x

     这个方程叫做估计线性方程(estimated regression line)

     其中，b₀是估计线性方程的纵截距

               b₁是估计线性方程的斜率

               ŷ是在自变量x等于一个给定值的时候，y的估计值

 

10. 线性回归分析流程：

     

  

 

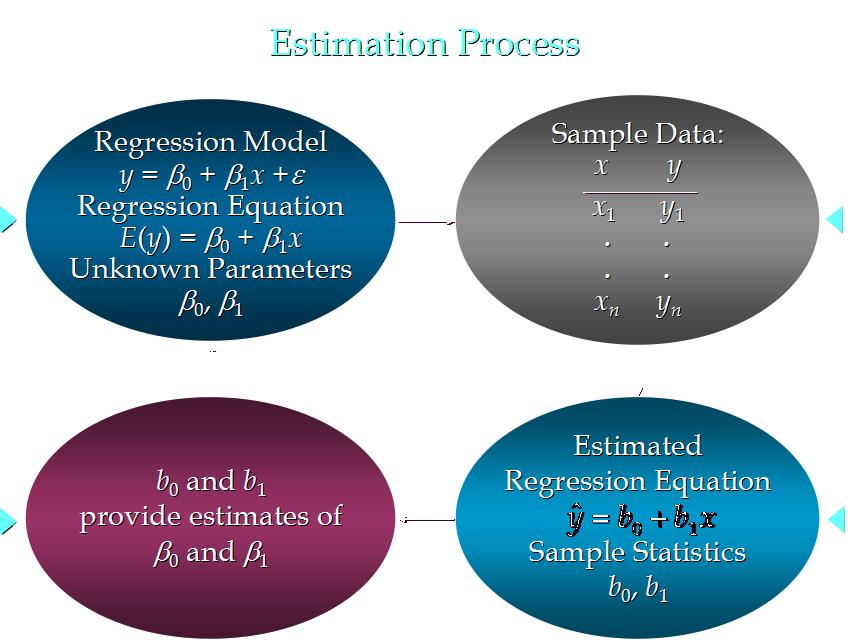
11. 关于偏差ε的假定

     11.1 是一个随机的变量，均值为0

     11.2 ε的方差(variance)对于所有的自变量x是一样的

     11.3 ε的值是独立的

     11.4 ε满足正态分布

 

 

多元回归分析：

1. 与简单线性回归区别(simple linear regression)

       多个自变量(x)

 

2. 多元回归模型

     y=β₀＋β_１x₁+β₂x₂+ ... +β_px_p+ε

    其中：β_0，β_１，β₂... β_p是参数

                 _{ε是误差值}

 

3. 多元回归方程

     E(y)=β₀＋β_１x₁+β₂x₂+ ... +β_px_p

 

_{4. 估计多元回归方程:}

     _{y_hat=b0＋b１x1+b2x2+ ... +bpxp}

 

    一个样本被用来计算β_0，β_１，β₂... β_p的点估计b_0, b_1, b_2,..., b_p

 

 

5. 估计流程  (与简单线性回归类似）

 

 

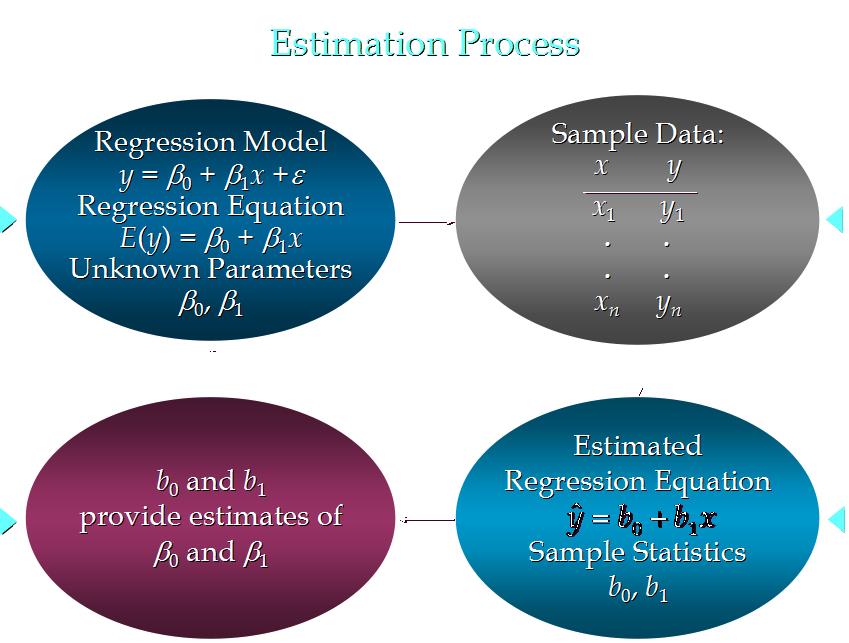
6. 估计方法

    使sum of squares最小    

     

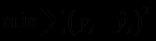
    运算与简单线性回归类似，涉及到线性代数和矩阵代数的运算