bp神经网络人口预测程序（matlab实现）

Posted 2023-05-17

1949年至2013年人口数为
54167
55196
56300
57482
58796
60266
61465
62828
64653
65994
67207
66207
65859
67295
69172
70499
72538
74542
76368
78534
80671
82992
85229
87177
89211
90859
92420
93717
94974
96259
97542
98705
100072
101654
103008
104357
105851
107507
109300
111026
112704
114333
115823
117171
118517
119850
121121
122389
123626
124761
125786
126743
127627
128453
129227
129988
130756
131448
132129
132802
134480
135030
135770
136460
137510
（万人）2014-2020年人口数，matlab程序怎么编？

x=[54167    
55196    
56300    
57482    
58796    
60266    
61465    
62828    
64653    
65994    
67207    
66207    
65859    
67295    
69172    
70499    
72538    
74542    
76368    
78534    
80671    
82992    
85229    
87177    
89211    
 90859    
 92420    
 93717    
 94974    
 96259    
 97542    
 98705    
100072    
101654    
103008    
104357    
105851    
107507    
109300    
111026    
112704    
114333    
115823    
117171    
118517    
119850    
121121    
122389    
123626    
124761    
125786    
126743    
127627    
128453    
129227    
129988    
130756    
131448    
132129    
132802    
134480    
135030    
135770    
136460    
137510]';
% 该脚本用来做NAR神经网络预测
% 作者：Macer程
lag=3;    % 自回归阶数
iinput=x; % x为原始序列（行向量）
n=length(iinput);

%准备输入和输出数据
inputs=zeros(lag,n-lag);
for i=1:n-lag
    inputs(:,i)=iinput(i:i+lag-1)';
end
targets=x(lag+1:end);

%创建网络
hiddenLayerSize = 10; %隐藏层神经元个数
net = fitnet(hiddenLayerSize);

% 避免过拟合，划分训练，测试和验证数据的比例
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;

%训练网络
[net,tr] = train(net,inputs,targets);
%% 根据图表判断拟合好坏
yn=net(inputs);
errors=targets-yn;
figure, ploterrcorr(errors)                      %绘制误差的自相关情况（20lags）
figure, parcorr(errors)                          %绘制偏相关情况
%[h,pValue,stat,cValue]= lbqtest(errors)         %Ljung－Box Q检验（20lags）
figure,plotresponse(con2seq(targets),con2seq(yn)) %看预测的趋势与原趋势
%figure, ploterrhist(errors)                      %误差直方图
%figure, plotperform(tr)                          %误差下降线


%% 下面预测往后预测几个时间段
fn=7;  %预测步数为fn。

f_in=iinput(n-lag+1:end)';
f_out=zeros(1,fn);  %预测输出
% 多步预测时，用下面的循环将网络输出重新输入
for i=1:fn
    f_out(i)=net(f_in);
    f_in=[f_in(2:end);f_out(i)];
end
% 画出预测图
figure,plot(1949:2013,iinput,'b',2013:2020,[iinput(end),f_out],'r')

                                             图1自相关

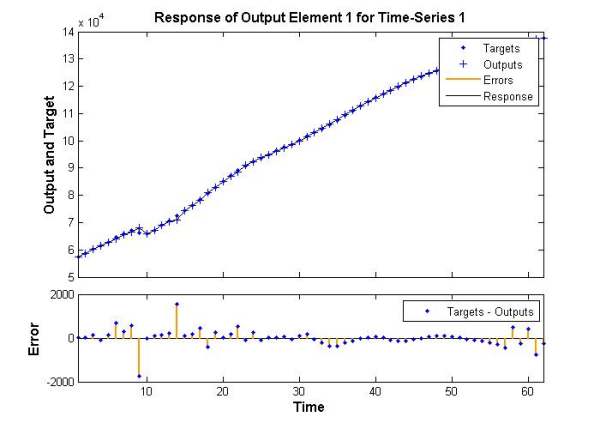
                                                 图2误差

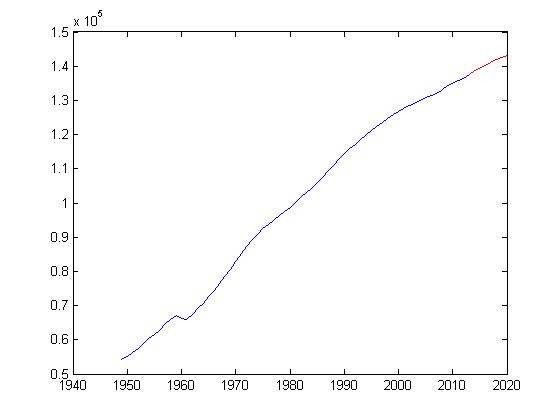
                                                  图3预测

      上面的程序是可以通用的，只要你根据自己需要是可以修改用在其他地方的，基本思想就是用前lag年的人口数来预测下一年的人口，至于lag等于几你是可以自己改的。还有在对结果好坏的判断中，仅仅看误差图是不够的，如果是一个好的预测，那么自相关性图中除了0阶自相关外，其他的自相关系数系数都不应该超过上下置信区间。还有其他的统计量和图表都都写在”%“后面了，如果需要，去掉就可用。最后的预测值为f_out，我的预测值为

138701.065269972    139467.632609654    140207.209707364    141210.109373609    141981.285378849    142461.332139592    143056.073139776

参考技术A x=[54167 55196 56300 57482 58796 60266 61465 62828 64653 65994 67207 66207 65859 67295 69172 70499 72538 74542 76368 78534 80671 82992 85229 87177 89211 90859 92420 93717 94974 96259 97542 98705 100072 101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124761 125786 126743 127627 128453 129227 129988 130756 131448 132129 132802 134480 135030 135770 136460 137510]';
>> lag=3;
>> iinput=x;
>> n=length(iinput);
>> inputs=zeros(lag,n-lag);
>> for i=1:n-lag
inputs(:,i)=iinput(i:i+lag-1)';
end
>> targets=x(lag+1:end);
>> hiddenLayerSize = 10;
>> net = fitnet(hiddenLayerSize);
>> net.divideParam.trainRatio = 70/100;
>> net.divideParam.valRatio = 15/100;
>> net.divideParam.testRatio = 15/100;
>> [net,tr] = train(net,inputs,targets);
Error using trainlm (line 109)
Inputs and targets have different numbers of samples.

Error in network/train (line 106)
[net,tr] = feval(net.trainFcn,net,X,T,Xi,Ai,EW,net.trainParam);

>> yn=net(inputs);
Error using network/sim (line 130)
Input 1 size does not match net.inputs1.size.

Error in network/subsref (line 14)
[v,out2,out3] = sim(vin,subs:);
运行不了啊

BP预测基于鲸鱼算法优化BP神经网络实现数据预测matlab源码

  一、 BP神经网络预测算法简介

说明：1.1节主要是概括和帮助理解考虑影响因素的BP神经网络算法原理，即常规的BP模型训练原理讲解（可根据自身掌握的知识是否跳过）。1.2节开始讲基于历史值影响的BP神经网络预测模型。

使用BP神经网络进行预测时，从考虑的输入指标角度，主要有两类模型：

1.1 受相关指标影响的BP神经网络算法原理

如图一所示，使用MATLAB的newff函数训练BP时，可以看到大部分情况是三层的神经网络（即输入层，隐含层，输出层）。这里帮助理解下神经网络原理：
1）输入层：相当于人的五官，五官获取外部信息，对应神经网络模型input端口接收输入数据的过程。
2）隐含层：对应人的大脑，大脑对五官传递来的数据进行分析和思考，神经网络的隐含层hidden Layer对输入层传来的数据x进行映射，简单理解为一个公式hiddenLayer_output=F(w*x+b)。其中，w、b叫做权重、阈值参数，F()为映射规则，也叫激活函数，hiddenLayer_output是隐含层对于传来的数据映射的输出值。换句话说，隐含层对于输入的影响因素数据x进行了映射，产生了映射值。
3）输出层：可以对应为人的四肢，大脑对五官传来的信息经过思考（隐含层映射）之后，再控制四肢执行动作（向外部作出响应）。类似地，BP神经网络的输出层对hiddenLayer_output再次进行映射，outputLayer_output=w *hiddenLayer_output+b。其中，w、b为权重、阈值参数，outputLayer_output是神经网络输出层的输出值（也叫仿真值、预测值）（理解为，人脑对外的执行动作，比如婴儿拍打桌子）。
4）梯度下降算法：通过计算outputLayer_output和神经网络模型传入的y值之间的偏差，使用算法来相应调整权重和阈值等参数。这个过程，可以理解为婴儿拍打桌子，打偏了，根据偏离的距离远近，来调整身体使得再次挥动的胳膊不断靠近桌子，最终打中。

再举个例子来加深理解：

图一所示BP神经网络，具备输入层、隐含层和输出层。BP是如何通过这三层结构来实现输出层的输出值outputLayer_output，不断逼近给定的y值，从而训练得到一个精准的模型的呢？

从图中串起来的端口，可以想到一个过程：坐地铁，将图一想象为一条地铁线路。王某某坐地铁回家的一天：在input起点站上车，中途经过了很多站（hiddenLayer），然后发现坐过头了（outputLayer对应现在的位置），那么王某某将会根据现在的位置离家（目标Target）的距离（误差Error），返回到中途的地铁站（hiddenLayer）重新坐地铁（误差反向传递，使用梯度下降算法更新w和b），如果王某某又一次发生失误，那么将再次进行这个调整的过程。

从在婴儿拍打桌子和王某某坐地铁的例子中，思考问题：BP的完整训练，需要先传入数据给input，再经过隐含层的映射，输出层得到BP仿真值，根据仿真值与目标值的误差，来调整参数，使得仿真值不断逼近目标值。比如（1）婴儿受到了外界的干扰因素（x），从而作出反应拍桌（predict），大脑不断的调整胳膊位置，控制四肢拍准（y、Target）。（2）王某某上车点（x），过站点（predict），不断返回中途站来调整位置，到家（y、Target）。

在这些环节中，涉及了影响因素数据x，目标值数据y（Target）。根据x，y，使用BP算法来寻求x与y之间存在的规律，实现由x来映射逼近y，这就是BP神经网络算法的作用。再多说一句，上述讲的过程，都是BP模型训练，那么最终得到的模型虽然训练准确，但是找到的规律（bp network）是否准确与可靠呢。于是，我们再给x1到训练好的bp network中，得到相应的BP输出值（预测值）predict1，通过作图，计算Mse，Mape，R方等指标，来对比predict1和y1的接近程度，就可以知道模型是否预测准确。这是BP模型的测试过程，即实现对数据的预测，并且对比实际值检验预测是否准确。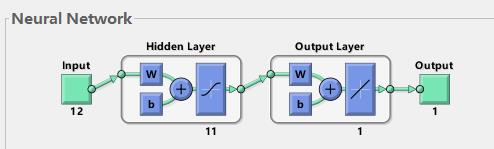

图一 3层BP神经网络结构图

1.2 基于历史值影响的BP神经网络

以电力负荷预测问题为例，进行两种模型的区分。在预测某个时间段内的电力负荷时：

一种做法，是考虑 t 时刻的气候因素指标，比如该时刻的空气湿度x1，温度x2，以及节假日x3等的影响，对 t 时刻的负荷值进行预测。这是前面1.1所说的模型。

另一种做法，是认为电力负荷值的变化，与时间相关，比如认为t-1，t-2，t-3时刻的电力负荷值与t时刻的负荷值有关系，即满足公式y(t)=F(y(t-1),y(t-2),y(t-3))。采用BP神经网络进行训练模型时，则输入到神经网络的影响因素值为历史负荷值y(t-1),y(t-2),y(t-3)，特别地，3叫做自回归阶数或者延迟。给到神经网络中的目标输出值为y(t)。

 二、鲸鱼算法

1、启发

鲸鱼优化算法 (whale optimization algorithm,WOA)是 2016 年由澳大利亚格里菲斯大学的Mirjalili等提出的一种新的群体智能优化算法，其优点在于操作简单、参数少以及跳出局部最优的能力强。 ​

2、包围猎物

座头鲸能识别猎物的位置并围着它们转。由于最优位置在搜索空间中的位置是未知的，WOA算法假设当前的最佳候选解是目标猎物或接近最优解。在定义了最佳候选解之后，其他候选位置将尝试向最佳位置移动并更新其位置。此行为由以下等式表示：

3、狩猎行为

根据座头鲸的狩猎行为，它是以螺旋运动游向猎物，故狩猎行为的数学模型如下：

4、搜索猎物

数学模型如下：

三、WOA优化BP神经网络的步骤

Step1：初始化BP神经网络的权值和阈值
Step2：计算鲸鱼优化算法的决策变量长度，选取均方误差作为优化的目标函数。
Step3：设置算法停止准则，使用遗传优化算法优化神经网络的权值和阈值参数。
Step4：将优化得到的权值和阈值参数赋给BP神经网络。
Step5：优化后的BP神经网络训练与测试，与优化前的BP神经网络进行误差分析和精度对比。

三、演示代码

%__________________________________________
% fobj = @YourCostFunction
% dim = number of your variables
% Max_iteration = maximum number of generations
% SearchAgents_no = number of search agents
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n
% If all the variables have equal lower bound you can just
% define lb and ub as two single number numbers

% To run ALO: [Best_score,Best_pos,cg_curve]=ALO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)

% The Whale Optimization Algorithm
function [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj,handles,value)

% initialize position vector and score for the leader
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems


%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iter);

t=0;% Loop counter

% Main loop
while t<Max_iter
    for i=1:size(Positions,1)
        
        % Return back the search agents that go beyond the boundaries of the search space
        Flag4ub=Positions(i,:)>ub;
        Flag4lb=Positions(i,:)<lb;
        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        
        % Calculate objective function for each search agent
        fitness=fobj(Positions(i,:));
        All_fitness(1,i)=fitness;
        
        % Update the leader
        if fitness<Leader_score % Change this to > for maximization problem
            Leader_score=fitness; % Update alpha
            Leader_pos=Positions(i,:);
        end
        
    end
    
    a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)
    
    % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)
    a2=-1+t*((-1)/Max_iter);
    
    % Update the Position of search agents 
    for i=1:size(Positions,1)
        r1=rand(); % r1 is a random number in [0,1]
        r2=rand(); % r2 is a random number in [0,1]
        
        A=2*a*r1-a;  % Eq. (2.3) in the paper
        C=2*r2;      % Eq. (2.4) in the paper
        
        
        b=1;               %  parameters in Eq. (2.5)
        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)
        
        p = rand();        % p in Eq. (2.6)
        
        for j=1:size(Positions,2)
            
            if p<0.5   
                if abs(A)>=1
                    rand_leader_index = floor(SearchAgents_no*rand()+1);
                    X_rand = Positions(rand_leader_index, :);
                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)
                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)
                    
                elseif abs(A)<1
                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)
                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)
                end
                
            elseif p>=0.5
              
                distance2Leader=abs(Leader_pos(j)-Positions(i,j));
                % Eq. (2.5)
                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);
                
            end
            
        end
    end
    
    t=t+1;
    Convergence_curve(t)=Leader_score;
    
    if t>2
        line([t-1 t], [Convergence_curve(t-1) Convergence_curve(t)],'Color','b')
        xlabel('Iteration');
        ylabel('Best score obtained so far');        
        drawnow
    end
 
    
    set(handles.itertext,'String', ['The current iteration is ', num2str(t)])
    set(handles.optimumtext,'String', ['The current optimal value is ', num2str(Leader_score)])
    if value==1
        hold on
        scatter(t*ones(1,SearchAgents_no),All_fitness,'.','k')
    end
    
    
    
    
end

四、仿真结果

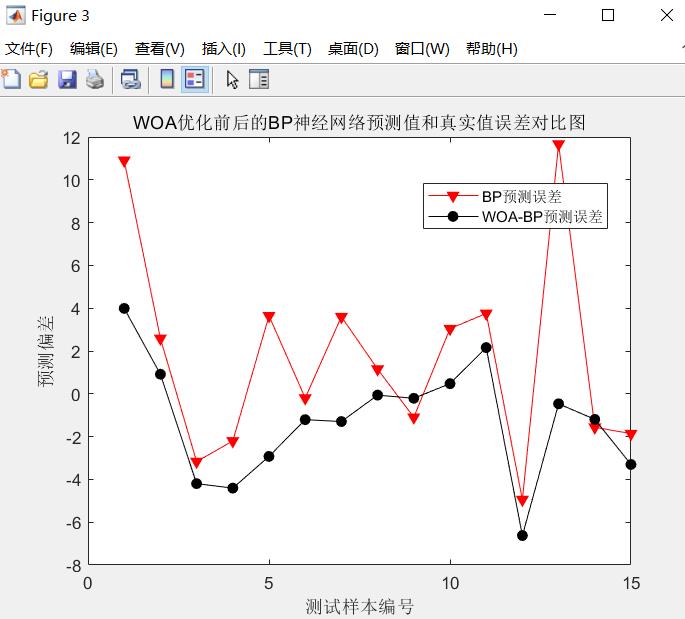
五、参考文献及代码私信博主

《基于BP神经网络的宁夏水资源需求量预测》