CSU 1804: 有向无环图 拓扑排序 图论

Posted 2020-09-30 九月旧约

1804: 有向无环图

Submit Page    Summary    Time Limit: 5 Sec     Memory Limit: 128 Mb     Submitted: 716     Solved: 298    

---

Description

Bobo 有一个 n 个点，m 条边的有向无环图（即对于任意点 v，不存在从点 v 开始、点 v 结束的路径）。

为了方便，点用 1,2,…,n 编号。 设 count(x,y) 表示点 x 到点 y 不同的路径数量（规定 count(x,x)=0），Bobo 想知道

 

 

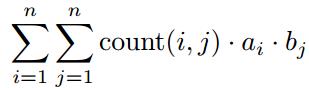
除以 (109+7) 的余数。

其中，ai,bj 是给定的数列。

 

Input

输入包含不超过 15 组数据。

每组数据的第一行包含两个整数 n,m (1≤n,m≤105).

接下来 n 行的第 i 行包含两个整数 ai,bi (0≤ai,bi≤109).

最后 m 行的第 i 行包含两个整数 ui,vi，代表一条从点 ui 到 vi 的边 (1≤ui,vi≤n)。

 

Output

对于每组数据，输出一个整数表示要求的值。

Sample Input

3 3
1 1
1 1
1 1
1 2
1 3
2 3
2 2
1 0
0 2
1 2
1 2
2 1
500000000 0
0 500000000
1 2

Sample Output

4
4
250000014

Hint

Source

湖南省第十二届大学生计算机程序设计竞赛

 

先将每个点i对应的count(i,j)*bj算出来然后乘ai，累加就是答案，注意这里要类似拓扑排序那样，不过要倒着做，避免后效性

参考博客 http://blog.csdn.net/qq_21057881/article/details/52431139

 

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define LL long long
const int maxn = 1e5+7;
const int mod = 1e9+7;
vector<int>e[maxn];
int a[maxn],b[maxn],d[maxn];
int ans[maxn];
int main(){
    int n,m;
    while(cin >> n >> m){
        for(int i=1;i<=n;i++){
            e[i].clear();
        }
        memset(d,0,sizeof(d));
        memset(ans,0,sizeof(ans));
        for(int i=1;i<=n;i++){
            cin >> a[i] >> b[i];
        }
        for(int i=1;i<=m;i++){
            int u,v;
            cin >> u >> v;
            e[v].push_back(u);
            d[u]++;//终点为u的路径的条数
        }
        queue<int> q;
        for(int i=1;i<=n;i++){
            if(d[i] == 0){//把终点为i的路径数为0的点加入队列
                q.push(i);
            }
        }
        while(!q.empty()){
            int v = q.front();
            q.pop();
            for(int i=0;i<e[v].size();i++){
                int u = e[v][i];
                ans[u] = (ans[u] + (ans[v] + b[v])%mod)%mod;
                //之所以是加b[v]，是因为乘是相当于整体而言，一条就是1*b[v]相当于加b[v]
                d[u]--;
                if(d[u] == 0){
                    q.push(u);
                }
            }
        }
        LL res = 0;
        for(int i=1;i<=n;i++){
            res = (res + 1LL*ans[i]*a[i]%mod)%mod;
        }
        cout << res << endl;
    }
    return 0;
}