孟德尔分离定律建模

Posted 2020-09-30

版权所有，QQ：231469242

孟德尔分离定律建模

law of segregation 分离定理

segregation分离

 

 

 

 

算法：

 

 

 

 

 

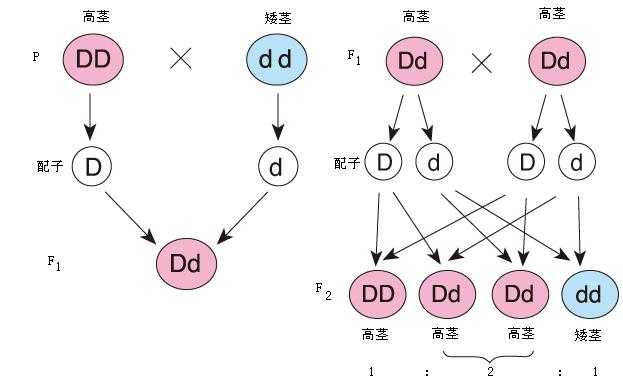
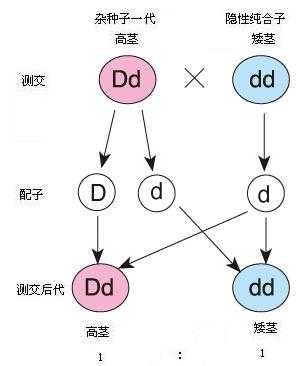
模拟孟德尔分离定理

 

#coding=utf-8
#law of segregation 孟德尔分离定理

import math,random,pylab

#试验次数
n=1000

#三类实验对象
#显性遗传因子
dominant_hereditary_factor=‘D‘
#隐性遗传因子
recessive_hereditary_factor=‘d‘
#遗传因子列表
list_hereditary_factor=[dominant_hereditary_factor,recessive_hereditary_factor]

#纯种高茎
high_pure=[dominant_hereditary_factor,dominant_hereditary_factor]
#纯种矮茎
low_pure=[recessive_hereditary_factor,recessive_hereditary_factor]
#杂种高茎
cross_high=[dominant_hereditary_factor,recessive_hereditary_factor]

#配子时，随机选出一个遗传因子

def Random_hereditary_factor(list_hereditary_factor):
#真随机数
r=random.SystemRandom()
#随机抽出一个遗传因子
random_hereditary_factor=r.choice(list_hereditary_factor)
return random_hereditary_factor

 

#配子过程
def Son(list1,list2):
son=[]
#纯高茎中抽取一个遗传因子
factor1=Random_hereditary_factor(list1)
son.append(factor1)
#纯矮茎中抽取一个遗传因子
factor2=Random_hereditary_factor(list2)
son.append(factor2)
return son

#配子性状判断，例如是高还是矮
def Character_analysis(list1,list2):
son=Son(list1,list2)
#print ‘son:‘,son
#如果线性遗传因子在配子中，返回显性性状
if dominant_hereditary_factor in son:
character="dominant_character"

#否则返回隐性性状
else:
character="recessive_character"

return character

 

#实验n次,观察高茎与矮茎数量比
def Count_test(n,list1,list2):
count_dominant=0
count_recessive=0
for i in range(n):
analysis1=Character_analysis(list1,list2)
if analysis1=="dominant_character":
count_dominant+=1
if analysis1=="recessive_character":
count_recessive+=1

ration=count_recessive*1.0/count_dominant
return ration

def Print(n,ratio_pureHigh_pureLow,ratio_crossHigh_crossHigh,ratio_crossHigh_pureLow):
print ‘n:‘,n
print ‘ratio_pureHigh_pureLow:‘,ratio_pureHigh_pureLow
print ‘ratio_crossHigh_crossHigh:‘,ratio_crossHigh_crossHigh
print ‘ratio_crossHigh_pureLow:‘,ratio_crossHigh_pureLow

#绘图前准备，得到多次实验的比例系数集合
def List_ratio(n,list1,list2):
list_ration=[]
for i in range(n):
ration=Count_test(n,list1,list2)
list_ration.append(ration)

return list_ration

#实验1：纯种高茎与纯种矮茎的数量比
#list_ratio1=List_ratio(n,high_pure,low_pure)
#实验2：杂种高茎与杂种高茎的数量比
#list_ratio2=List_ratio(n,cross_high,cross_high)
#实验3：杂种高茎和纯种矮茎的数量比
#list_ratio3=List_ratio(n,cross_high,low_pure)

#实验1：纯种高茎与纯种矮茎的数量比
ratio_pureHigh_pureLow=Count_test(n,high_pure,low_pure)

#实验2：杂种高茎与杂种高茎的数量比
#ratio_crossHigh_crossHigh=Count_test(n,cross_high,cross_high)

#实验3：杂种高茎和纯种矮茎的数量比
#ratio_crossHigh_pureLow=Count_test(n,cross_high,low_pure)

#Print(n,ratio_pureHigh_pureLow,ratio_crossHigh_crossHigh,ratio_crossHigh_pureLow)

 

 

 

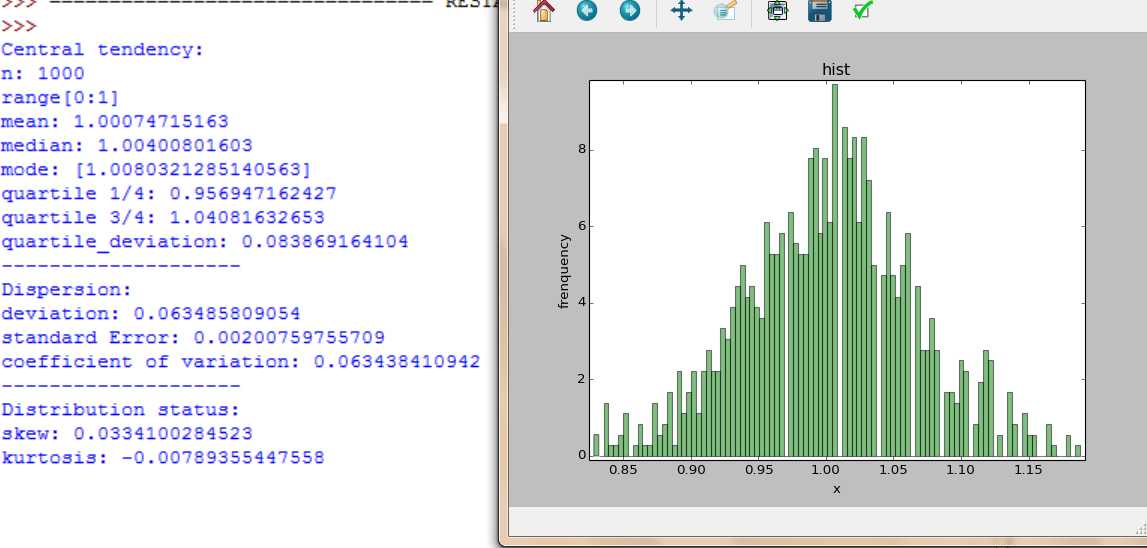
描述统计孟德尔分离定理

杂种高茎与杂种高茎

 

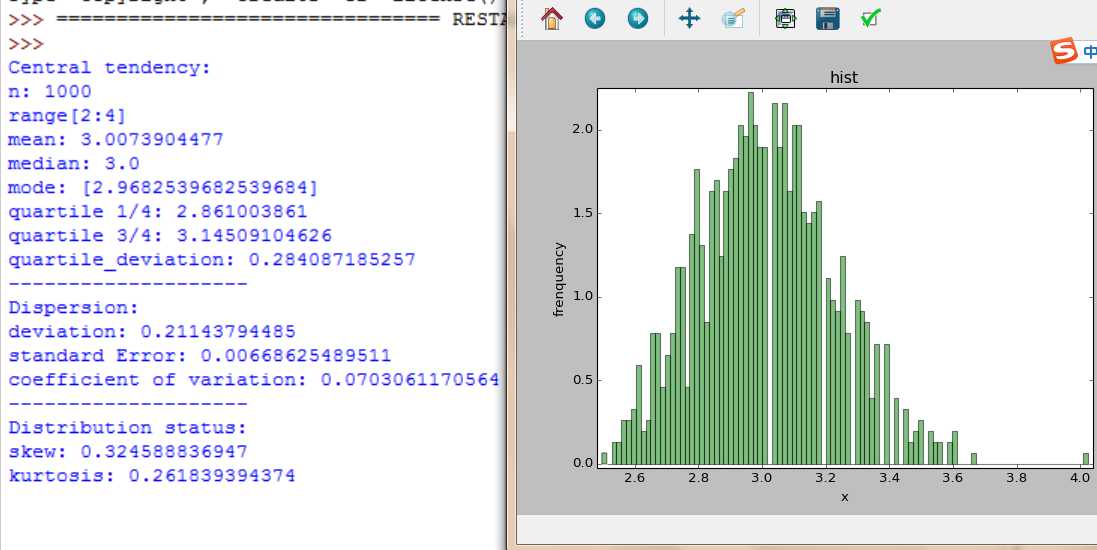
纯种高茎与纯种矮茎

 

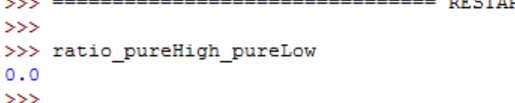
杂种高茎与纯种矮茎

 

 

 

#coding=utf-8
# mode 函数有问题
import math,numpy,pylab,distribution_status,statistics_functions,quartile,Law_of_segregation
#list1=[2.96,2.84,3.01,3.15,2.95,2.82,3.14]
#list1=[19,15,29,25,24,23,21,38,22,18,30,20,19,19,16,23,27,22,34,24,41,20,31,17,23]
#list1=[5.5,6.5,6.7,6.8,7.1,7.3,7.4,7.8,7.8]
#list1=[164,167,168,165,170,165,164,168,164,162,163,166,167,166,165]
#list1=[129,130,129,130,131,130,129,127,128,128,127,128,128,125,132]
#list1=[125,126,126,127,126,128,127,126,127,127,125,126,116,126,125]
list1=Law_of_segregation.list_ratio1
n=len(list1)
mean=statistics_functions.Mean(list1)
median=statistics_functions.Median(list1)
mode=statistics_functions.Mode(list1)
deviation=statistics_functions.Deviation(list1)
standardError=statistics_functions.Standard_error_of_the_mean(list1)
coefficient_of_variation=statistics_functions.Coefficient_of_variation(list1)

max1=max(list1)
min1=min(list1)

q_l=quartile.Quartile(list1,‘q_l‘)
q_u=quartile.Quartile(list1,‘q_u‘)
quartile_deviation=quartile.Quartile_deviation(list1)

skew=distribution_status.Skew(list1)
kurtosis=distribution_status.Kurtosis(list1)

print "Central tendency:"
print "n:",n
print "range[%d:%d]" %(min1,max1)
print "mean:",mean
print "median:",median
print "mode:",mode
print "quartile 1/4:",q_l
print "quartile 3/4:",q_u
print "quartile_deviation:",quartile_deviation

print "-"*20
print "Dispersion:"
print "deviation:",deviation
print "standard Error:",standardError
print "coefficient of variation:",coefficient_of_variation

print "-"*20
print "Distribution status:"
print "skew:",skew
print "kurtosis:",kurtosis

 

#绘图
def Draw(list1):
for i in list1:
x=i[0]
y=i[1]
pylab.plot(x,y,‘r--‘)
pylab.xlabel(‘x‘)
pylab.ylabel(‘y‘)
pylab.title("descriptive statistics")
pylab.grid(True)
# Pad margins so that markers don‘t get clipped by the axes,让点不与坐标轴重合
pylab.margins(0.05)
pylab.show()

def Draw_hist(list1):
#facecolor表面颜色
pylab.hist(list1,bins=100,normed=1,facecolor=‘green‘,alpha=0.5)
pylab.xlabel(‘x‘)
pylab.ylabel(‘frenquency‘)
pylab.title(‘hist‘)
pylab.margins(0.01)
pylab.show()

 

#数组中不重复数字
#list_noneRepeat=statistics_functions.List_noneRepeat(list1)
#不重复数字频率
#frequency=statistics_functions.Frequence(list1)

#dict_mean_frequency=dict(zip(list_noneRepeat,frequency))

#list_mean_frequency=dict_mean_frequency.items()

#Draw(list_mean_frequency)

Draw_hist(list1)