UVa 11149 Power of Matrix (矩阵快速幂，倍增法或构造矩阵)

Posted 2020-09-30 dwtfukgv

题意：求A + A^2 + A^3 + ... + A^m。

析：主要是两种方式，第一种是倍增法，把A + A^2 + A^3 + ... + A^m，拆成两部分，一部分是（E + A^(m/2)）（A + A^2 + A^3 + ... + A^(m/2)），然后依次计算下去，就可以分解，logn的复杂度分解，注意要分奇偶。

另一种是直接构造矩阵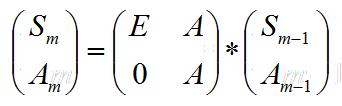，，然后就可以用辞阵快速幂计算了，注意要用分块矩阵的乘法。

代码如下：

倍增法：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#define debug() puts("++++");
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const double inf = 0x3f3f3f3f3f3f;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 1e3 + 10;
const int mod = 10;
const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, 1, 0, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
    return r > 0 && r <= n && c > 0 && c <= m;
}

struct Matrix{
  int a[40][40];
  int n;

  friend Matrix operator + (const Matrix &lhs, const Matrix &rhs){
    Matrix res;
    res.n = lhs.n;
    for(int i = 0; i < lhs.n; ++i)
      for(int j = 0; j < lhs.n; ++j)
        res.a[i][j] = (lhs.a[i][j] + rhs.a[i][j]) % mod;
    return res;
  }

  friend Matrix operator * (const Matrix &lhs, const Matrix &rhs){
    Matrix res;
    res.n = lhs.n;
    for(int i = 0; i < lhs.n; ++i)
      for(int j = 0; j < lhs.n; ++j){
        res.a[i][j] = 0;
        for(int k = 0; k < lhs.n; ++k)
          res.a[i][j] += lhs.a[i][k] * rhs.a[k][j];
        res.a[i][j] %= mod;
      }
    return res;
  }
};

Matrix E;

Matrix fast_pow(Matrix a, int m){
  Matrix res;
  res.n = n;
  memset(res.a, 0, sizeof res.a);
  for(int i = 0; i < res.n; ++i)
    res.a[i][i] = 1;
  while(m){
    if(m & 1)  res = res * a;
    m >>= 1;
    a = a * a;
  }
  return res;
}

Matrix dfs(int m, Matrix x){
  if(m == 1)  return x;
  if(m == 0)  return E;
  Matrix ans = (E + fast_pow(x, m/2)) * dfs(m/2, x);
  if(m & 1)  ans = ans + fast_pow(x, m);
  return ans;
}

int main(){
  while(scanf("%d %d", &n, &m) == 2 && n){
    Matrix x;  x.n = n;
    E.n = n;
    memset(E.a, 0, sizeof E.a);
    for(int i = 0; i < n; ++i)
      E.a[i][i] = 1;
    for(int i = 0; i < n; ++i)
      for(int j = 0; j < n; ++j){
        scanf("%d", &x.a[i][j]);
        x.a[i][j] %= mod;
      }

    Matrix ans = dfs(m, x);
    for(int i = 0; i < n; ++i)
      for(int j = 0; j < n; ++j)
        if(j + 1 == n)  printf("%d\\n", ans.a[i][j]);
        else printf("%d ", ans.a[i][j]);
    printf("\\n");
  }
  return 0;
}

　　

构造法：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#define debug() puts("++++");
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const double inf = 0x3f3f3f3f3f3f;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 1e3 + 10;
const int mod = 10;
const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, 1, 0, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
    return r > 0 && r <= n && c > 0 && c <= m;
}

struct Node{
  int a[80][80];

  friend void add(const Node &lhs, const Node &rhs, Node &res, int x, int y, int l, int r){
    for(int i = x; i < y; ++i)
      for(int j = l; j < r; ++j)
        res.a[i][j] = (lhs.a[i-x][j-l] + rhs.a[i-x][j-l]) % mod;
  }

  friend void solve(int x, int y, int l, int r, int p, int q, const Node &lhs, const Node &rhs, Node &res){
    for(int i = x; i < y; ++i)
      for(int j = l; j < r; ++j){
        res.a[i-x][j-l] = 0;
        for(int k = p; k < q; ++k)
          res.a[i-x][j-l] += lhs.a[i][k] * rhs.a[k][j];
      }
  }

  friend Node operator * (const Node &lhs, const Node &rhs){
    Node res, x, y;
    solve(0, n, 0, n, 0, n, lhs, rhs, x);
    solve(0, n, 0, n, n, n+n, lhs, rhs, y);
    add(x, y, res, 0, n, 0, n);

    solve(0, n, n, n+n, 0, n, lhs, rhs, x);
    solve(0, n, n, n+n, n, n+n, lhs, rhs, y);
    add(x, y, res, 0, n, n, n+n);

    solve(n, n+n, 0, n, 0, n, lhs, rhs, x);
    solve(n, n+n, 0, n, n, n+n, lhs, rhs, y);
    add(x, y, res, n, n+n, 0, n);

    solve(n, n+n, n, n+n, 0, n, lhs, rhs, x);
    solve(n, n+n, n, n+n, n, n+n, lhs, rhs, y);
    add(x, y, res, n, n+n, n, n+n);

    return res;
  }
};

Node fast_pow(Node a, int m){
  Node res;
  memset(res.a, 0, sizeof res.a);
  for(int i = 0; i < n; ++i)
    res.a[i][i] = res.a[i+n][i] = 1;

  while(m){
    if(m & 1)  res = res * a;
    m >>= 1;
    a = a * a;
  }
  return res;
}

int main(){
  while(scanf("%d %d", &n, &m) == 2 && n){
    Node x, y;
    memset(y.a, 0, sizeof y.a);
    for(int i = 0; i < n; ++i)
      for(int j = n; j < n+n; ++j){
        scanf("%d", &y.a[i][j]);
        y.a[i][j] %= mod;
      }
    for(int i = 0; i < n; ++i)
      y.a[i][i] = 1;
    for(int i = n; i < n + n; ++i)
      for(int j = n; j < n + n; ++j)
        y.a[i][j] = y.a[i-n][j];
    memset(x.a, 0, sizeof x.a);
    for(int i = n; i < n+n; ++i)
      x.a[i][i-n] = 1;

    Node ans = fast_pow(y, m);

    if(m)  ans = ans * x;
    for(int i = 0; i < n; ++i)
      for(int j = 0; j < n; ++j)
        if(j == n-1)  printf("%d\\n", ans.a[i][j]);
        else  printf("%d ", ans.a[i][j]);
    printf("\\n");
  }
  return 0;
}