关联分析（购物篮子分析market basket analysis）R练习

Posted 2020-09-29 积水成渊数据分析

关联分析(association analysis)又称关联挖掘，就是在交易数据、关系数据或其他信息载体中，查找存在于项目集合或对象集合之间的频繁模式。简言之，关联分析是发现数据库中不同项之间的联系。

与回归问题、分类问题不同，关联算法不能进行预测，但可以用于无监督的知识发现，寻找数据之间的关联性。由于其本身不需要提前标记数据，算法实施也很便捷，但是关联算法除了从定性的角度衡量其有效性以外，尚无一个简单的方法来客观地衡量其性能。

基本概念：

1、A→B的支持度：事件A,B同时发生的概率support =P（AB）

2、A→B的置信度：发生事件A基础上发生事件B的概率confidence = P(B|A)=P（AB）/P（A）=support（A→B）/support（A）

3、提升度：confidence（A→B）/support（A）

4、K项集：如果事件A中包含K个元素，称这个事件A为K项集，并且事件A满足最小支持度阈值的事件称为频繁K项集

主要算法：Apriori

算法思想：Apriori 算法利用了关于频繁项集性质的一个简单先验信念：一个频繁项集的所有子集必须是频繁的。逆否命题：如果一个项集是非频繁的，那么它的所有超集也是非频繁的。

算法原理：

1、计算出单个元素的支持度，然后选出单个元素置信度大于我们要求的数值，

2、增加单个元素组合的个数，只要组合项的支持度大于我们要求的数值就把它加到我们的频繁项集中，依次递归。

3、根据计算的支持度选出来的频繁项集来生成关联规则。

算法流程：

• 收集数据：使用任何方法
• 准备数据：任意数据类型都可以，因为我们只保存集合
• 分析数据：使用任何方法
• 训练算法：使用Apriori算法来找到频繁项集
• 测试算法：不需要测试过程
• 使用算法：用于发现频繁项集以及物品之间的关联规则

举个例子：数据集某超市购物订单，即A顾客购买了几款产品、B几款......，引入稀疏矩阵处理

> library(arules)
Loading required package: Matrix

Attaching package: ‘arules’
The following objects are masked from ‘package:base’:

    abbreviate, write
> groceries <- read.transactions(\'groceries.csv\', sep = \',\')
> groceries
transactions in sparse format with
 9835 transactions (rows) and #订单数量9835条
 169 items (columns) #商品类型169种

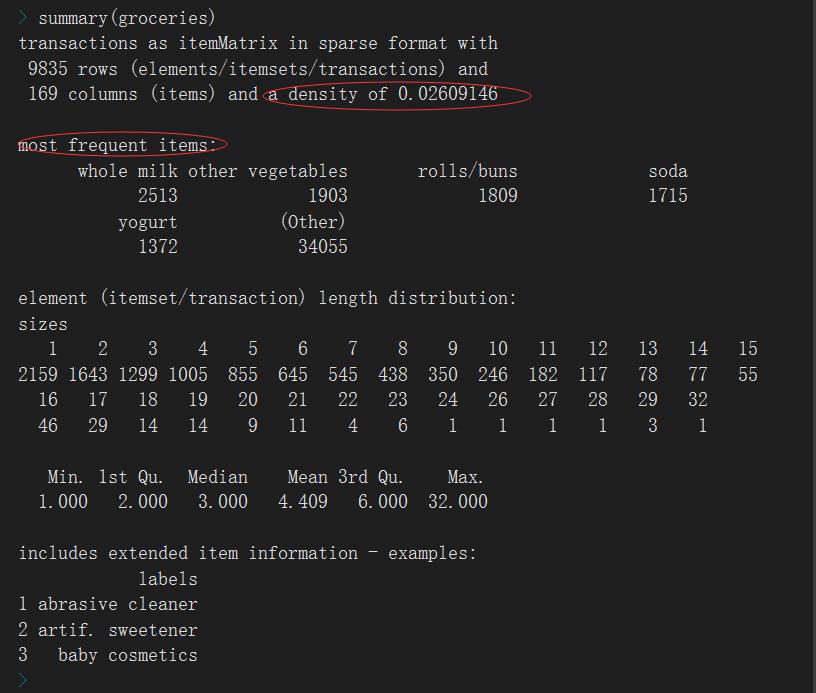
非零单元比例：a density of 0.02609146

常购商品：most frequent items

交易中包含商品种类分布：element (itemset/transaction) length distribution，也就是说有多少客户买了多少件产品，买1件产品的订单有2159个

 数据探索

> inspect(groceries[1:5,])#查看数据格式
    items                     
[1] {citrus fruit,            
     margarine,               
     ready soups,             
     semi-finished bread}     
[2] {coffee,                  
     tropical fruit,          
     yogurt}                  
[3] {whole milk}              
[4] {cream cheese,            
     meat spreads,            
     pip fruit,               
     yogurt}                  
[5] {condensed milk,          
     long life bakery product,
     other vegetables,        
     whole milk}              

> item <- itemFrequency(groceries)#查看商品支持度
+ item[order(item, decreasing = T)][1:10]
      whole milk other vegetables       rolls/buns             soda 
      0.25551601       0.19349263       0.18393493       0.17437722 
          yogurt    bottled water  root vegetables   tropical fruit 
      0.13950178       0.11052364       0.10899847       0.10493137 
   shopping bags          sausage 
      0.09852567       0.09395018 

> itemFrequencyPlot(groceries, support = 0.1)#绘制支持度大于0.1的商品

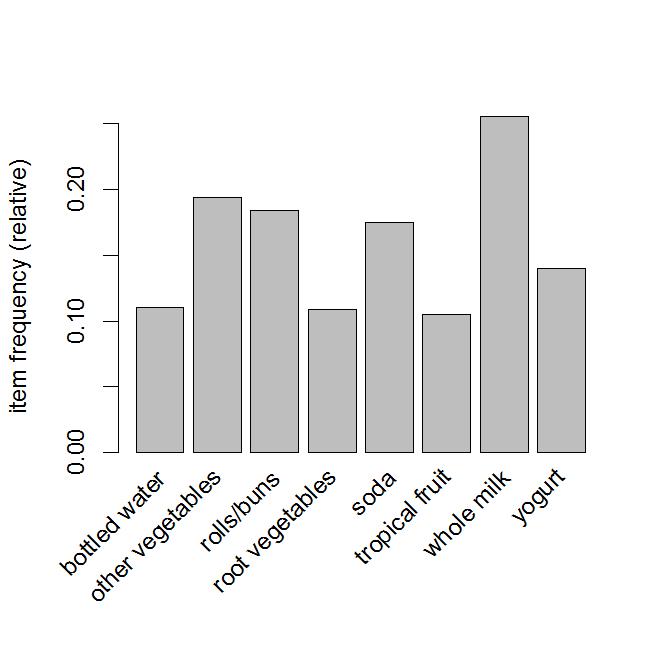
> itemFrequencyPlot(groceries, topN = 20)#卖得最好的20种商品

 

 

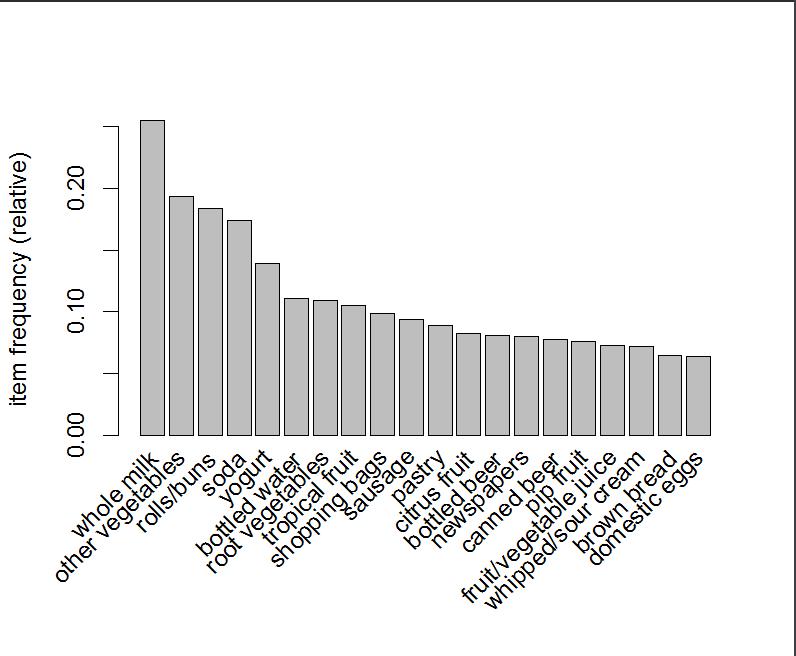
训练模型

> apriori(groceries) #不指定参数默认
Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime
        0.8    0.1    1 none FALSE            TRUE       5
 support minlen maxlen target   ext
     0.1      1     10  rules FALSE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 983 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.01s].
sorting and recoding items ... [8 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 done [0.00s].
writing ... [0 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].
set of 0 rules 

默认参数下没有发现规则，调整支持度、置信度

 

> apriori(groceries,parameter = list(support=0.01,confidence=0.2,minlen=2))
Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime
        0.2    0.1    1 none FALSE            TRUE       5
 support minlen maxlen target   ext
    0.01      2     10  rules FALSE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 98 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.02s].
sorting and recoding items ... [88 item(s)] done [0.00s].
creating transaction tree ... done [0.01s].
checking subsets of size 1 2 3 4 done [0.01s].
writing ... [231 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].
set of 231 rules 
> 
> groceryrules <- apriori(groceries, parameter = list(support = 0.006, confidence = 0.25, minlen = 2))
+ groceryrules
Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime support minlen maxlen
       0.25    0.1    1 none FALSE            TRUE       5   0.006      2     10
 target   ext
  rules FALSE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 59 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
sorting and recoding items ... [109 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 done [0.00s].
writing ... [463 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].
set of 463 rules 

规则提取（假设提取的是最后这个规则，只是举例，实际生产中，可以根据不同的规则估算销售额可能的增长，以销售额最高的那个规则组合作为输出，或者是进行灰度测试）

> summary(groceryrules)
set of 463 rules

rule length distribution (lhs + rhs):sizes
  2   3   4 
150 297  16 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  2.000   2.000   3.000   2.711   3.000   4.000 

summary of quality measures:
    support           confidence          lift       
 Min.   :0.006101   Min.   :0.2500   Min.   :0.9932  
 1st Qu.:0.007117   1st Qu.:0.2971   1st Qu.:1.6229  
 Median :0.008744   Median :0.3554   Median :1.9332  
 Mean   :0.011539   Mean   :0.3786   Mean   :2.0351  
 3rd Qu.:0.012303   3rd Qu.:0.4495   3rd Qu.:2.3565  
 Max.   :0.074835   Max.   :0.6600   Max.   :3.9565  

mining info:
      data ntransactions support confidence
 groceries          9835   0.006       0.25

> inspect(sort(groceryrules, by = "lift")[1:5])
    lhs                   rhs                      support confidence     lift
[1] {herbs}            => {root vegetables}    0.007015760  0.4312500 3.956477
[2] {berries}          => {whipped/sour cream} 0.009049314  0.2721713 3.796886
[3] {other vegetables,                                                        
     tropical fruit,                                                          
     whole milk}       => {root vegetables}    0.007015760  0.4107143 3.768074
[4] {beef,                                                                    
     other vegetables} => {root vegetables}    0.007930859  0.4020619 3.688692
[5] {other vegetables,                                                        
     tropical fruit}   => {pip fruit}          0.009456024  0.2634561 3.482649

提取指定关联规则

> berryrules <- subset(groceryrules, items %in% "berries")
> inspect(berryrules)
    lhs          rhs                  support     confidence lift    
[1] {berries} => {whipped/sour cream} 0.009049314 0.2721713  3.796886
[2] {berries} => {yogurt}             0.010574479 0.3180428  2.279848
[3] {berries} => {other vegetables}   0.010269446 0.3088685  1.596280
[4] {berries} => {whole milk}         0.011794611 0.3547401  1.388328

输出所有规则

> groceryrules_df <- as(groceryrules, "data.frame")
+ head(groceryrules_df)
                               rules     support confidence     lift
1    {potted plants} => {whole milk} 0.006914082  0.4000000 1.565460
2            {pasta} => {whole milk} 0.006100661  0.4054054 1.586614
3       {herbs} => {root vegetables} 0.007015760  0.4312500 3.956477
4      {herbs} => {other vegetables} 0.007727504  0.4750000 2.454874
5            {herbs} => {whole milk} 0.007727504  0.4750000 1.858983
6 {processed cheese} => {whole milk} 0.007015760  0.4233129 1.656698

> write(groceryrules,
+       file = \'groceryrules.csv\',
+       sep = \',\',
+       row.names = F,
+       quote = T)