TensorRT--INT8量化

Posted 2023-05-15

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了TensorRT--INT8量化相关的知识，希望对你有一定的参考价值。

参考技术A 现有深度学习框架在训练深度神经网络时，往往都会使用 FP32 的数据精度来表示权值、偏置、激活值等。但是当网络很深时，网络参数量大，计算量大。如此大的计算量，如果中间值都使用 FP32 的精度来计算的话，势必会很费时间。这对于嵌入式设备或者移动设备来说，简直就是噩梦。

因此解决此问题的方法之一就是在部署推理时（inference）使用低精度数据，比如INT8，注意此处只是针对推理阶段，训练时仍然使用 FP32 的精度。除此之外，当然还有模型压缩之类的方法。为什么进行低精度推理不会造成太大的精度损失可以参考 Why are Eight Bits Enough for Deep Neural Networks? 这篇博文。

最简单的映射方式就是线性映射（或称线性量化，linear quantization）, 就是说映射前后的关系满足下式：

是每一层上每一个 tensor 的换算系数或称比例因子（scaling factor），因此现在的问题就变成了如何确定比例因子。简单的做法如下图所示：

简单的将一个 tensor 中的 -|max| 和 |max| FP32 映射为 -127 和 127，中间值按照线性关系进行映射，这种映射关系为不饱和的（No saturation ），对称的。但是这样做会导致比较大的精度损失。

TensorRT的做法如下图所示：

我们需要一个衡量指标来衡量不同的 INT8 分布与原来的 FP32 分布之间的差异程度。这个衡量指标就是相对熵（relative entropy），又称为KL散度（Kullback–Leibler divergence，简称KLD）。每一层的 tensor 的 |T| 值都是不一样的，确定每一层的 |T| 值的过程称为校准（Calibration ）。

从验证集选取一个子集作为校准集（Calibration Dataset），校准集应该具有代表性，多样性，最好是验证集的一个子集，不应该只是分类类别的一小部分。

通信原理实验七基于Matlab的均匀量化和非均匀量化

一、实验类型

设计性实验

二、实验目的

1.掌握均匀量化原理和非均匀量化原理。
2.掌握量化信噪比的基本概念。
3. 理解量化级数、量化方法与量化信噪比的关系。

三、实验原理

1.均匀量化原理

设模拟信号的取值范围是[a,b],量化电平数是M,那么均匀量化的量化间隔是：

量化取间的端点是：

若量化输出电平取量化间隔的中点，则
，

显然，量化输出电平和量化前的信号的抽样值一般是不同的，即量化输出电平有误差，这个误差称谓量化噪声（quantization noise）,并用信号功率之比（简称为信号量噪比），衡量此误差对信号的影响的大小。对给定的信号最大幅度，量化电平数越多，量化的噪声越小，信号量噪比越高。
在均匀量化时，量化噪声功率的平均值可以用下面的式子表示：

式子中的为模拟信号的抽样值，即，为量化信号值，为信号的抽样值的概率密度。为求统计平均值。为量化电平数。
信号的平均功率可表示为：

若已知信号的概率密度函数，则由公式可计算出平均信号量噪声比。
计算时可用如下公式直接计算，对于具有均匀概率密度的信号则有：
。
所以平均信号量噪比为：

当输入信号为 正弦信号 是，量化信噪比表示为:

在实际的应用中，对于给定的量化器的，量化电平数M和量化间隔都是给定的。所以，量化噪声也是给定的，但是，信号的强度可能是随时间变化的，像语音信号就是这样子的。当信号小时，信号的量化信噪比也小。所以这种均匀量化器对于小输入信号很不利。所以一般对小信号采用非均匀量化。

2.非均匀量化

为了克服均匀量化的缺点，实际中，往往采用非均匀量化。非均匀量化是根据信号的不同区间来确定量化间隔的。实现方法如图1 所示。

			图1非均匀量化实现过程

A律对数压缩特性具有如下的关系，在国际标准中取=87.6。

式中，为归一化的压缩器输入电压，为归一化压缩器输出电压，为压扩参数，表示压缩程度。
13折线特性就是近似于=87.6时的律压缩特性，律压缩特性的非均匀量化信噪比：

其中为信噪比改善度。

其中为信号有效值。
补充： 1.求对数的函数
log(x)：求x的自然对数，即ln(x)。
log2(x)：求x的以2为底的对数，即log 2 (x)。
log10(x)：求x的以10为底的对数，即lg(x)。
2.在样值数较多时，量化噪声平均功率和信号功率时，可通过用mean函数求均方值来计算：

,所用函数 mean(e.^2）；
: mean(s.^2）

三、例子演示仿真步骤

1、均匀量化

例【1】（1）产生一个周期的正弦波，以1000Hz频率进行采样，并进行8级均匀量化，用plot函数在同一张图上绘出原信号和量化后的信号。

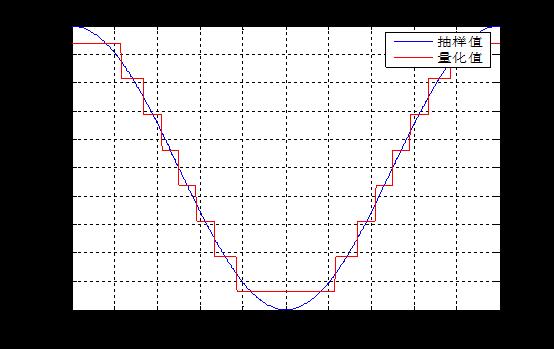
%均匀量化例1中（1）
clear all
fs=1000;
dt=1/fs;
M=8;
Am=1;
t=0:dt:1;
x=Am*cos(2*pi*t);
v=(max(x)-min(x))/M;
m(1)=min(x);
for i=1:M
    m(i+1)=m(i)+v;
    q(i)=(m(i)+m(i+1))/2;
end
   for j=1:length(x)
       for i=1:M-1
           if(x(j)>=m(i)&x(j)<m(i+1))
            lh(j)=q(i); 
         end
        if(x(j)>=m(M))
            lh(j)=q(M);
         end
       end
  end
plot(t,x);
grid on; 
hold on
plot(t,lh,'r');
legend('抽样值','量化值');
xlabel('图1 余弦信号的均匀量化')

（2）以32Hz频率对例1中的x(t)进行采样，并进行8级均匀量化。用stem函数绘出正弦波波形样值图，量化后的样值图、量化误差图。

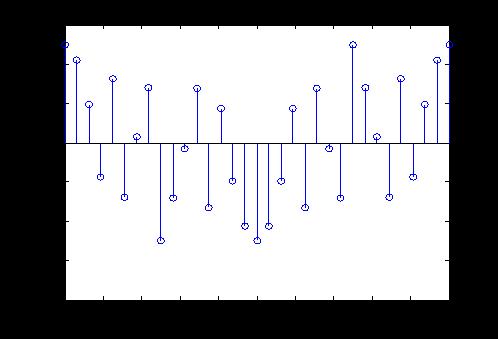
%均匀量化例1中（2），抽样频率32Hz
clear all
fs=32;
dt=1/fs;
M=8;
Am=1;
t=0:dt:1;
x=Am*cos(2*pi*t);
v=(max(x)-min(x))/M;%量化间隔
m(1)=min(x);
for i=1:M
    m(i+1)=m(i)+v;
    q(i)=(m(i)+m(i+1))/2;%量化电平值
end
   for j=1:length(x)
       for i=1:M-1
           if(x(j)>=m(i)&x(j)<m(i+1))
            lh(j)=q(i); 
         end
        if(x(j)>=m(M))
            lh(j)=q(M);
         end
       end
    e(j)=x(j)-lh(j);% 量化误差值
end
stem(t,x);
grid on; 
hold on
stem(t,lh,'r');
legend('抽样值','量化值');
xlabel('图2 均匀量化离散图')
figure(2)
stem(t,e);
xlabel('图3 均匀量化的量化误差图')

（3）以2000Hz对x(t)进行采样，改变量化级数，分别仿真得到编码位数为2～8位时的量化信噪比，绘出量化信噪比随编码位数变化的曲线。另外绘出理论的量化信噪比曲线进行比较。

%均匀量化例1中（3）不同编码位数的量化信噪比
clear all
fs=2000;
dt=1/fs;
n=2:8;
M=2.^n;
Am=1;
t=0:dt:1;
x=Am*cos(2*pi*t);
for k=1:length(M)
v=(max(x)-min(x))/M(k);
m(1)=min(x);
for i=1:M(k)
    m(i+1)=m(i)+v;
    q(i)=(m(i)+m(i+1))/2;
end
   for j=1:length(x)
       for i=1:M(k)-1
           if(x(j)>=m(i)&x(j)<m(i+1))
            lh(j)=q(i); 
         end
        if(x(j)>=m(M(k)))
            lh(j)=q(M(k));
         end
       end
    e(j)=x(j)-lh(j);
end
s=mean(x.^2);
N=mean(e.^2);
lzb(k)=10*log10(s/N);%均匀量化量噪比的仿真值
lzb2(k)=6.02*n(k)+1.76;%%均匀量化量噪比的理论值
end
plot(n,lzb,'o-');
hold on;
plot(n,lzb2,'ro-');
legend('仿真值','理论值');
xlabel('图4 不同编码位数的均匀量化信噪比')

例【2】产生一个周期的正弦波，对x(t)按A律进行压缩，然后以32Hz频率进行抽样，再进行8级均匀量化。压扩参数A=87.6。绘出压缩前后的信号波形图(用plot函数)、样值图、量化后的样值图(后两个用stem函数)。

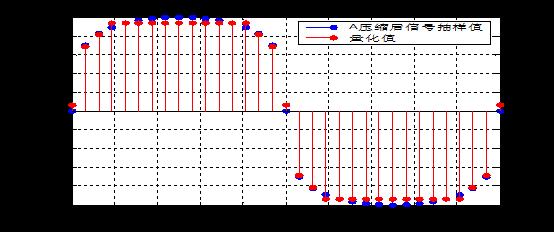
clear all
fs=32;
dt=1/fs;
M=16;
Am=1;
t=0:dt:1;
x=Am*sin(2*pi*t);
x=x/max(x);
A=87.6;
for i=1:length(x)
   if(abs(x(i))>=0&abs(x(i))<=1/A)
       if(x(i)>0)
       y(i)=A*x(i)/(1+log(A));
      else y(i)=-A*x(i)/(1+log(A));
       end
   else
       if(x(i)>0)
         y(i)=(1+log(A*x(i)))/(1+log(A));
      else y(i)=-(1+log(A*x(i)))/(1+log(A));
       end
   end
end
plot(t,x);
grid on; 
hold on
plot(t,y,'r')
legend('归一化后原信号','A律压缩后的信号');
xlabel('图1 抽样信号A律压缩')
v=2/M;
m(1)=-1;
for i=1:M
    m(i+1)=m(i)+v;
    q(i)=(m(i)+m(i+1))/2;
end
   for j=1:length(y)
       for i=1:M-1
           if(y(j)>=m(i)&y(j)<m(i+1))
            lh(j)=q(i); 
         end
        if(y(j)>=m(M))
            lh(j)=q(M);
         end
       end
    e(j)=y(j)-lh(j);
   end
figure(2)
stem(t,y,'filled');
grid on; 
hold on
stem(t,lh,'r','filled');
legend('A压缩后信号抽样值','量化值');
xlabel('图2 A律压缩后的抽样值和量化值')
figure(3)
stem(t,e);
xlabel('图3 A律压缩量化的量化误差图')

四、实验内容

对于输入信号为sin（t）信号进行抽样和均匀量化，改变抽样频率、量化级数和信号大小，根据MATLAB获得量化误差和量化信噪比。同一个坐标轴上画出原信号和已量化信号，比较着不同情况下的量化信噪比。
对于输入信号为sin（t）信号进行A压缩率的非均匀量化，改变抽样频率和信号大小，根据MATLAB获得量化误差和量化信噪比。同一个坐标轴上画出原信号和已量化信号，比较着不同情况下的量化信噪比。