顶点法向量从物体坐标系变换到世界坐标系

Posted 2020-06-26 bluebean

 3维网格模型的顶点的法向量一开始是定义在模型坐标系中的，在将模型布置在场景中后，根据光照模型计算颜色时需要用到顶点法向量，由于光照都是在世界坐标系中进行计算，这时用到的法向量也应该是定义在世界坐标系中。所以我们需要设法将顶点法向量从模型坐标系中转换到世界坐标系中。

我们已经知道通过缩放、旋转、平移三种基本操作合成的model矩阵可以将网格顶点坐标从模型坐标系中转换到世界坐标系中。那么这个model矩阵是否也可以将顶点法向量转换到世界坐标系呢？如果不行，那么需要找到一个可以完成这个任务的矩阵。

1.model矩阵是否可以用于转换法向量

答案：不行

 

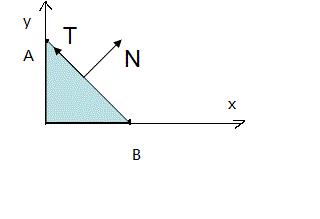
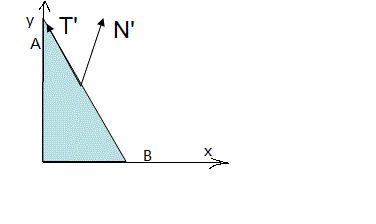
如图所示：图中的线段AB经过了缩放变换。上图中点A=(0,1) B=(1,0)，法向量N=(1,1)；下图中经过y坐标值放大两倍的变换后，法向量N=（1,2），而向量T‘=A-B=(-1,2)，法向量N’不再与线段AB垂直。

 

注：平移和选择变换并不会改变法向量与线段的垂直关系。

 

2.寻找用于变换法向量的通用矩阵

2.1 证明一个多边形的切向量经过model矩阵的变换后也是变换后的平面的切向量

 

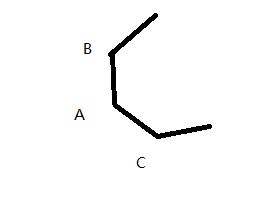
如图：多边形的其中三个顶点是A,B,C，则多变形的任意一个切向量可以表示为：

T=a*(B-A)+b*(C-A) 

a,b不同时为零

设model矩阵为M

所以经过变化后

T‘=M*T=a*(M*B-M*A)+b*(M*C-M*A)=a*(B’-A’)+b*(C’-A’)

所以经过model矩阵变化的切向量也是变换后的多边形的切向量

 

2.2 求解

设：在模型空间中，网格的某个三角面的切向量为t，法向量为n.

经过模型矩阵M的变换后，t’=Mt，t’仍是变换后的三角面的切向量。假定存在矩阵N，使用N变换法向量n，得到n’=Nn，使得n’是正确的世界坐标系中的法向量。N即是我们所要寻求的矩阵。

法向量垂直于切向量，所以有：

 

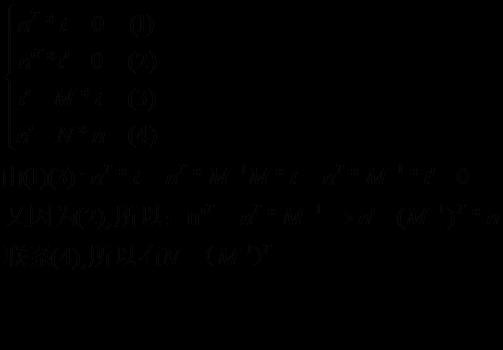
所以N是模型矩阵的逆矩阵的转置。

 

参考资料：《计算机图形学》第二版 Peter Shirley著 第六章第二节