『cs231n』作业2选讲_通过代码理解卷积层&池化层

Posted 2020-09-29

卷积层

卷积层向前传播示意图：

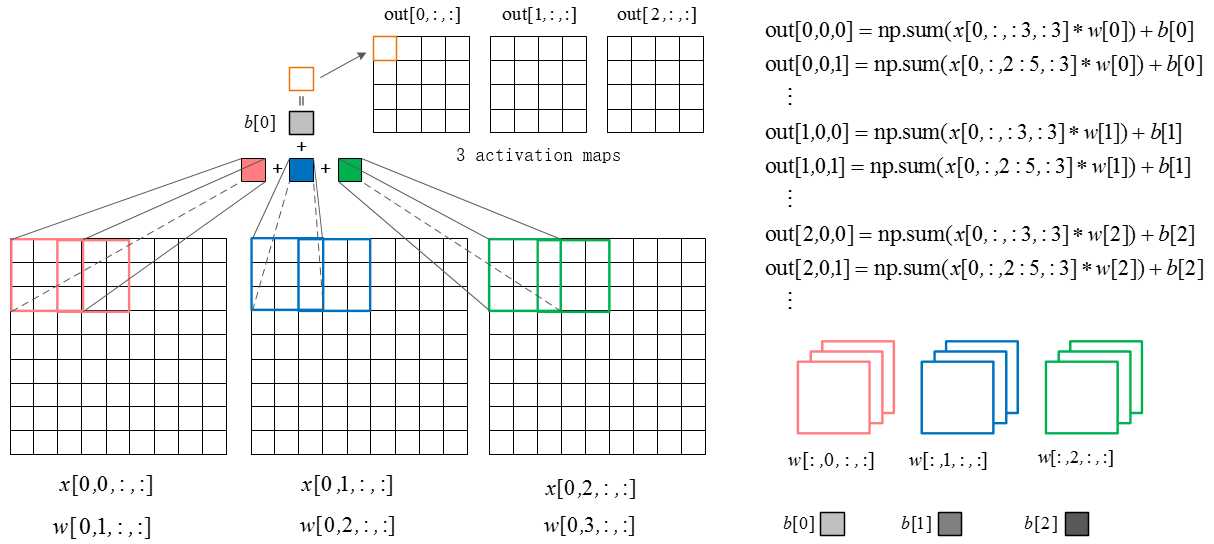
def conv_forward_naive(x, w, b, conv_param):
  """
  A naive implementation of the forward pass for a convolutional layer.

  The input consists of N data points, each with C channels, height H and width
  W. We convolve each input with F different filters, where each filter spans
  all C channels and has height HH and width HH.

  Input:
  - x: Input data of shape (N, C, H, W)
  - w: Filter weights of shape (F, C, HH, WW)
  - b: Biases, of shape (F,)
  - conv_param: A dictionary with the following keys:
    - ‘stride‘: The number of pixels between adjacent receptive fields in the
      horizontal and vertical directions.
    - ‘pad‘: The number of pixels that will be used to zero-pad the input.

  Returns a tuple of:
  - out: Output data, of shape (N, F, H‘, W‘) where H‘ and W‘ are given by
    H‘ = 1 + (H + 2 * pad - HH) / stride
    W‘ = 1 + (W + 2 * pad - WW) / stride
  - cache: (x, w, b, conv_param)
  """
  out = None
  #############################################################################
  # TODO: Implement the convolutional forward pass.                           #
  # Hint: you can use the function np.pad for padding.                        #
  ############################################################################
  pad = conv_param[‘pad‘]  
  stride = conv_param[‘stride‘]
  N, C, H, W = x.shape
  F, _, HH, WW = w.shape
  H0 = 1 + (H + 2 * pad - HH) / stride
  W0 = 1 + (W + 2 * pad - WW) / stride
  x_pad = np.pad(x, ((0,0),(0,0),(pad,pad),(pad,pad)),‘constant‘)    # 填充后的输入
  out = np.zeros((N,F,H0,W0))                                        # 初始化的输出
    
  # 以输出的每一个像素点为单位写出其前传表达式
  for n in range(N):
    for f in range(F):
        for h0 in range(H0):
            for w0 in range(W0):
                out[n,f,h0,w0] = np.sum(x_pad[n,:,h0*stride:HH+h0*stride,w0*stride:WW+w0*stride] * w[f]) + b[f]
  #############################################################################
  #                             END OF YOUR CODE                              #
  #############################################################################
  cache = (x, w, b, conv_param)
  return out, cache

卷积层反向传播示意图：

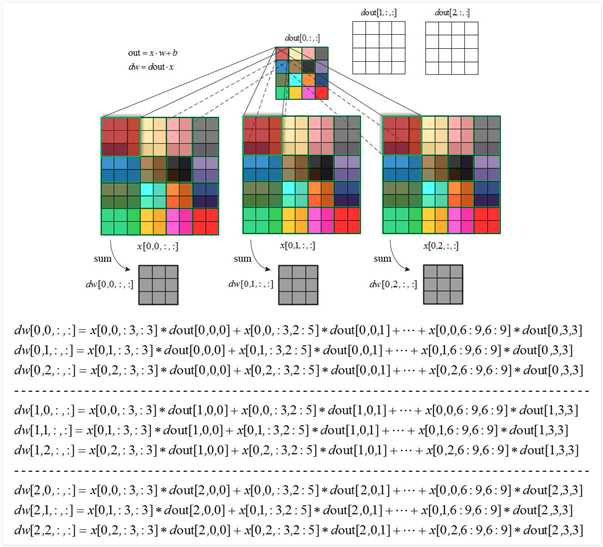
def conv_backward_naive(dout, cache):
  """
  A naive implementation of the backward pass for a convolutional layer.

  Inputs:
  - dout: Upstream derivatives.
  - cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive

  Returns a tuple of:
  - dx: Gradient with respect to x
  - dw: Gradient with respect to w
  - db: Gradient with respect to b
  """
  dx, dw, db = None, None, None
  #############################################################################
  # TODO: Implement the convolutional backward pass.                          #
  #############################################################################
  x, w, b, conv_param = cache
  pad = conv_param[‘pad‘]  
  stride = conv_param[‘stride‘]
  N, C, H, W = x.shape
  F, _, HH, WW = w.shape
  _, _, H0, W0 = out.shape
    
  x_pad = np.pad(x, [(0,0), (0,0), (pad,pad), (pad,pad)], ‘constant‘)
  dx, dw = np.zeros_like(x), np.zeros_like(w)
  dx_pad = np.pad(dx, [(0,0), (0,0), (pad,pad), (pad,pad)], ‘constant‘)   
  # 计算b的梯度(F,)
  db = np.sum(dout, axis=(0,2,3))    # dout:(N,F,H0,W0)
  # 以每一个dout点为基准计算其两个输入矩阵x(:,:,窗,窗)和w(f)的梯度，注意由于这两个矩阵都是多次参与运算，所以都是累加的关系
  for n in range(N):
    for f in range(F):
      for h0 in range(H0):
        for w0 in range(W0):
          x_win = x_pad[n,:,h0*stride:h0*stride+HH,w0*stride:w0*stride+WW]
          dw[f] += x_win * dout[n,f,h0,w0]
          dx_pad[n,:,h0*stride:h0*stride+HH,w0*stride:w0*stride+WW] += w[f] * dout[n,f,h0,w0]
  dx = dx_pad[:,:,pad:pad+H,pad:pad+W]
  #############################################################################
  #                             END OF YOUR CODE                              #
  #############################################################################
  return dx, dw, db

 池化层（亦下采样层）

池化层向前传播：

和卷积层类似，但是更简单一点，只要在对应feature map的原输入上取个窗口然后池化之即可，

def max_pool_forward_naive(x, pool_param):
    HH, WW = pool_param[‘pool_height‘], pool_param[‘pool_width‘]
    s = pool_param[‘stride‘]
    N, C, H, W = x.shape
    H_new = 1 + (H - HH) / s
    W_new = 1 + (W - WW) / s
    out = np.zeros((N, C, H_new, W_new))
    for i in xrange(N):    
        for j in xrange(C):        
            for k in xrange(H_new):            
                for l in xrange(W_new):                
                    window = x[i, j, k*s:HH+k*s, l*s:WW+l*s] 
                    out[i, j, k, l] = np.max(window)

    cache = (x, pool_param)

    return out, cache

 池化层反向传播：

反向传播的时候也是还原窗口，除最大值处继承上层梯度外（也就是说本层梯度为零），其他位置置零。

池化层没有过滤器，只有dx梯度，且x的窗口不像卷积层会重叠，所以不用累加，

def max_pool_backward_naive(dout, cache):
    x, pool_param = cache
    HH, WW = pool_param[‘pool_height‘], pool_param[‘pool_width‘]
    s = pool_param[‘stride‘]
    N, C, H, W = x.shape
    H_new = 1 + (H - HH) / s
    W_new = 1 + (W - WW) / s
    dx = np.zeros_like(x)
    for i in xrange(N):    
        for j in xrange(C):        
            for k in xrange(H_new):            
                for l in xrange(W_new):                
                    window = x[i, j, k*s:HH+k*s, l*s:WW+l*s]                
                    m = np.max(window)               
                    dx[i, j, k*s:HH+k*s, l*s:WW+l*s] = (window == m) * dout[i, j, k, l]

    return dx