Rain in ACStar HDU-3340

Posted 2020-09-29 大米饼

·你正从AC星球返回，天又下起凸包雨，只好到线段树下躲雨。

·英文题，述大意：

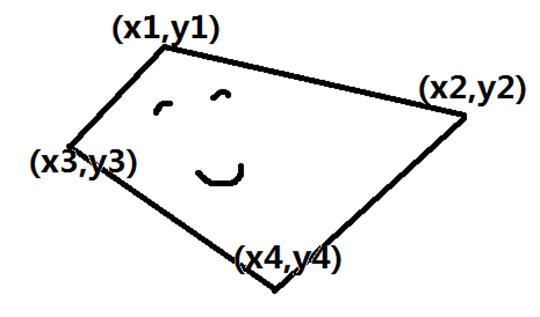
      一个竖直平面的美丽天空，会下凸包雨。凸包雨指的是边数为3~6的多边形，并且每一个它都遵守一个神奇定律，那就是自己不会有两个横坐标相同的点（即每个凸包自己的顶点不会出现在一条垂直于x轴的直线上）。现在有Q个操作：第一种是放置一个凸包雨（即输入其边数，并从其横坐标最小点开始顺时针读入顶点坐标[x,y<=1000000000]）；第二种是询问，即读入l,r来询问我们横坐标在[l,r]之间的雨滴的面积总和（被切开的雨也算），也就是求[l,r]的凸包总面积。(Q<=25000)

·分析：

      凸包雨很多，询问很多。我们需要使用数据结构加以维护。请选择一款你是喜爱的数据结构满足以下条件：①你喜欢②可以维护区间的凸包面积！

但问题是这是一个二维的问题，我们需要加以转化，目的是使每个凸包的面积便于使用某种美妙的数据结构维护。

      尝试将计算形形色色的凸包的方法单一化，我们从一个简单可爱的四边形入手：现在知道其顶点坐标，怎么求面积？

                                              

 

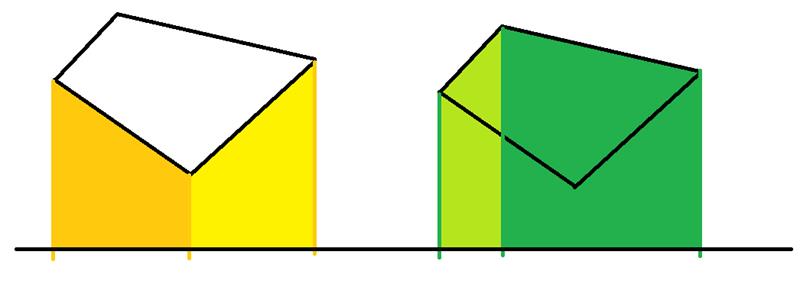
       我们探索面积求法的目的需要再次说明：使得对各种多边形面积计算的方法单一化。从坐标的角度思考，我们可以想到作差法（这很常用），但是选择它的一个主要原因是，可以将任意多边形分解为几个梯形的面积加加减减的美好结果（当然，矩形,三角形这里可看做特殊的梯形，因为它们的面积计算同样满足：S=(l₁+l₂)*h/2）。即：将面积计算方法单一化。如图：

 

 

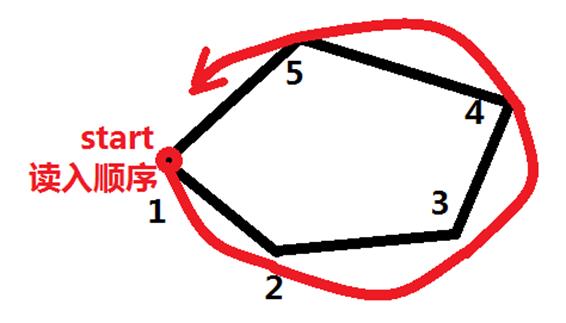
            如美丽的图：我们发现，四边形面积就可以使用两个绿色梯形的面积减去两个黄色梯形的面积。很开心发现这个结论。但是我们需要进一步推广，获得一个普遍的计算方式。我们需要快速确定什么该减什么时候该加。顺着输入的顺序（从最左边点的逆时针）如图：

                             

        按照读入顺序，我们根据上文结论，可以知道，这个多边形的面积是上顶点为(5 1)(4 5)的梯形面积和减去上顶点为(1 2)(2 3)(3 4)的梯形面积。接着你就惊奇地发现，有规律：按照逆时针顺序，对于一个点a,如果它的上一个点的横坐标比它小，那么以它俩为上顶点的梯形面积就要减去；反之，如果是横坐标大，则这个梯形的面积就要加上(想一想，很容易)。所以在读入后就可以按照这个方法了。

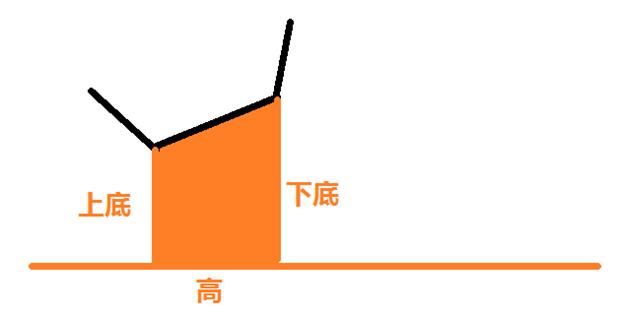
       怎么操作？现在我们获得了求梯形面积的方法，基于相邻每个点的坐标。这个时候就是数据结构了。对于一个梯形，就用小学的面积公式，意思说我们只需要维护上下底的长度（即两个点的纵坐标）。如个图：

                           

       你决定了，要使用线段树啦啦。实际上写代码时候，我们可以引入一个思想和一个变量来使得CODING更加美妙。思想是我们可以看做是线段树维护等差数列（注意维护等差数列的基本思路：维护左右端点和公差）。方法是引入公差，即凸包那一条边的斜率，这样便于计算在线段树PushDown的时候的中间数。

        线段树的特别的参数有：A(左端点加的值，即等差数列第一项)，B(左端点加的值),ratio(斜率),它们对应的Lazy数组是：a[],b[],G[],另外，需要维护一个Sum[]表示当前区间的面积和(面积加加减减)。例子在这里：(例如向区间[1,4]插入等差数列{1,2,3,4})

       最后是一些美妙的提醒和细节处理：

①注意在Lazy下放和线段树区间分裂时都可能会有取中项的操作

②离散化询问，以及点的横坐标（所以在计算的时候一定要调用原长）

③本题的一个线段树叶子结点是l+1==r表示一段小区间。

④在PushDown时和update到达指定区间时都需要计算Sum（即Sum[u]+=）

      剩下的都在代码里面，无比美妙。

 

 1 #define D double
 2 #define lch u<<1
 3 #include<stdio.h>
 4 #define rch u<<1|1
 5 #define M (l+r>>1)
 6 #include<algorithm>
 7 #define Up Sum[u]=Sum[lch]+Sum[rch]
 8 #define go(i,a,b) for(int i=a;i<=b;i++)
 9 #define Rar(a) a=lower_bound(T+1,T+n+1,a)-T
10 using namespace std;
11 const int N=250003;char c[N];
12 int C,m,t,tt,kk,k,n,len[N],T[N],I,J;
13 D A[N*4],B[N*4],Sum[N*4],G[N*4],ratio,ans;
14 struct Q{int l,r;}q[N];struct P{int x,y;}p[N][7];
15 D Cal(D a,int s,D rate){return 1.0*a+1.0*s*rate;}
16 void build(int u,int l,int r)
17 {
18     A[u]=B[u]=Sum[u]=G[u]=0;if(l+1==r)return;
19     build(lch,l,M);build(rch,M,r);
20 }
21 void Down(int u,int l,int r)
22 {
23     G[lch]+=G[u],G[rch]+=G[u];A[lch]+=A[u];B[rch]+=B[u];
24     D Z=Cal(A[u],T[M]-T[l],G[u]);
25     Sum[lch]+=1.0*(A[u]+Z)*(T[M]-T[l])/2;
26     Sum[rch]+=1.0*(Z+B[u])*(T[r]-T[M])/2;
27     B[lch]+=Z,A[rch]+=Z,A[u]=B[u]=G[u]=0;
28 }
29 void update(int u,int l,int r,int L,int R,D a,D b)
30 {
31     if(L<=l&&r<=R){A[u]+=a;B[u]+=b;G[u]+=ratio;
32     Sum[u]+=1.0*(a+b)*(T[r]-T[l])/2;return;}Down(u,l,r);
33     if(R<=M)update(lch,l,M,L,R,a,b);
34     else if(L>=M)update(rch,M,r,L,R,a,b);
35     else{D Z=Cal(a,T[M]-T[L],ratio);
36     update(lch,l,M,L,M,a,Z);update(rch,M,r,M,R,Z,b);}Up;
37 }
38 void query(int u,int l,int r,int L,int R)
39 {
40     if(L<=l&&r<=R){ans+=Sum[u];return;};Down(u,l,r);
41     if(L<M)query(lch,l,M,L,R);
42     if(R>M)query(rch,M,r,L,R);
43 }
44 int main(){scanf("%d",&C);while(C--&&scanf("%d",&m))
45 {
46     n=k=t=tt=kk=0;
47     go(i,1,m){scanf(" %c",&c[i]);
48     if(c[i]==\'R\'&&scanf("%d",&len[++t]))
49     go(j,1,len[t])scanf("%d%d",&p[t][j].x,&p[t][j].y),T[++n]=p[t][j].x;
50     if(c[i]==\'Q\'&&scanf("%d%d",&q[k].l,&q[++k].r))T[++n]=q[k].l,T[++n]=q[k].r;}
51             
52     sort(T+1,T+n+1);n=unique(T+1,T+n+1)-T-1;
53     go(i,1,k)Rar(q[i].l),Rar(q[i].r);build(1,1,n);
54     go(i,1,t)go(j,1,len[i])Rar(p[i][j].x);
55         
56     go(i,1,m)if(c[i]==\'R\'&&++tt)go(j,1,len[tt])
57     {
58         I=j,J=j!=len[tt]?j+1:1;
59         int x1=p[tt][I].x,y1=p[tt][I].y,x2=p[tt][J].x,y2=p[tt][J].y;
60         if(x1<x2)y1*=-1,y2*=-1;else swap(x1,x2),swap(y1,y2);
61         ratio=1.0*(y2-y1)/(T[x2]-T[x1]);update(1,1,n,x1,x2,y1,y2);
62     }
63     else ++kk,ans=0,query(1,1,n,q[kk].l,q[kk].r),printf("%.3f\\n",ans);        
64 }return 0;}//Paul_Guderian

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

人们在卑微地倒立，可楼群却都高高在上，

这是不能接受的事实，真实得就像梦境一样。————汪峰《不能接受的事实》