『cs231n』作业1问题1选讲_通过代码理解K近邻算法&交叉验证选择超参数参数

Posted 2020-09-29 叠加态的猫

K近邻，交叉验证，SVM

通过K近邻算法探究numpy向量运算提速

 茴香豆的“茴”字有... ...

使用三种计算图片距离的方式实现K近邻算法：

1.最为基础的双循环

2.利用numpy的broadca机制实现单循环

3.利用broadcast和矩阵的数学性质实现无循环

图片被拉伸为一维数组

X_train：(train_num, 一维数组)

X：(test_num, 一维数组)

方法验证

import numpy as np
a = np.array([[1,1,1],[2,2,2],[3,3,3]])
b = np.array([[4,4,4],[5,5,5],[6,6,6],[7,7,7]])

双循环：

dists = np.zeros((3,4))
for i in range(3):
    for j in range(4):
        dists[i][j] = np.sqrt(np.sum(np.square(a[i] - b[j])))
print(dists)

 [[  5.19615242   6.92820323   8.66025404  10.39230485]
 [  3.46410162   5.19615242   6.92820323   8.66025404]
 [  1.73205081   3.46410162   5.19615242   6.92820323]]

单循环：

dists=np.zeros((3,4))
for i in range(3):
    dists[i] = np.sqrt(np.sum(np.square(a[i] - b),axis=1))
print(dists)

[[  5.19615242   6.92820323   8.66025404  10.39230485]
 [  3.46410162   5.19615242   6.92820323   8.66025404]
 [  1.73205081   3.46410162   5.19615242   6.92820323]] 

无循环：

r1=(np.sum(np.square(a),axis=1)*(np.ones((b.shape[0],1)))).T
r2=np.sum(np.square(b),axis=1)*(np.ones((a.shape[0],1)))
r3=-2*np.dot(a,b.T)
print(np.sqrt(r1+r2+r3))

 [[  5.19615242   6.92820323   8.66025404  10.39230485]
 [  3.46410162   5.19615242   6.92820323   8.66025404]
 [  1.73205081   3.46410162   5.19615242   6.92820323]]

 无循环算法原理：

（注意，原理图-验证代码-实现程序 的变量并不严格一一对应，均有调整）

全代码实现如下：

import numpy as np

class KNearsNeighbor():
    def _init_(self):
        pass

    def train(self, x, y):
        self.X_train = x
        self.y_train = y
　　
    # 选择使用几个循环体的方式来计算距离
    def predict(self, X, k=1, num_loops=0):
        if num_loops == 0:
            dist = self.compute_distances_no_loops(X)
        elif num_loops == 1:
            dist = self.compute_distances_one_loops(X)
        elif num_loops == 2:
            dist = self.compute_distances_two_loops(X)
        else:
            raise ValueError(\'Invalid value %d\' % num_loops)
        return dist

    def compute_distances_two_loops(self, X):
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test, num_train))
        for i in range(num_test):
            for j in range(num_train):
                dists[i][j] = np.sqrt(np.sum(np.square(X[i] - self.X_train[j])))
        return dists
    def compute_distances_one_loops(self, X):
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test,num_train))
        for i in range(num_test):
                dists[i] = np.sqrt(np.sum(np.square(X[i] - self.X_train), axis=1))
        return dists

    def compute_distances_no_loops(self, X):
        # num_test = X.shape[0]
        # num_train = self.X_train.shape[0]
        # dists = np.zeros((num_test,num_train))
        dists = np.sqrt(-2*np.dot(X, self.X_train.T) +
                        np.sum(np.square(self.X_train), axis=1)*(np.ones((X.shape[0],1))) +
                               np.sum(np.square(X), axis=1)*(np.ones(X_train.shape[0],1)).T)
        return dists

　　 # 预测标签
    def predict_labels(self, dists, k=1):
        num_test = dists.shape[0]
        y_pred = np.zeros(num_test)
        for i in range(num_test):
            closest_y = self.y_train[np.argsort(dists[i])[:k]]  # 【【【按照距离给索引排序】取最近的k个索引】按照索引取训练标签】
            y_pred[i] = np.argmax(np.bincount(closest_y))       #  投票，注意np.bincount()和np.argmax()在投票上的妙用
        return y_pred

 交叉验证选择超参数k的取值

We have implemented(实施) the k-Nearest Neighbor classifier(分类) but we set the value k = 5 arbitrarily(武断地). We will now determine the best value of this hyperparameter with cross-validation(交叉验证).

import numpy as np
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []
################################################################################
# TODO:                                                                        #
# Split up the training data into folds. After splitting, X_train_folds and    #
# y_train_folds should each be lists of length num_folds, where                #
# y_train_folds[i] is the label vector for the points in X_train_folds[i].     #
# Hint: Look up the numpy array_split function.                                #
################################################################################
X_train_folds = np.split(X_train, num_folds)
y_train_folds = np.split(y_train, num_folds)
################################################################################
#                                 END OF YOUR CODE                             #
################################################################################

# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO:                                                                        #
# Perform k-fold cross validation to find the best value of k. For each        #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times,   #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all     #
# values of k in the k_to_accuracies dictionary.                               #
################################################################################

for k in k_choices:
    k_to_accuracies[k]=np.zeros(num_folds)
    for i in range(num_folds):
        Xtr = np.concatenate(
            (np.array(X_train_folds)[:i],np.array(X_train_folds)[(i+1):]),axis=0)
        ytr = np.concatenate(
            (np.array(y_train_folds)[:i],np.array(y_train_folds)[(i+1):]),axis=0)
        Xte = np.array(X_train_folds)[i]
        yte = np.array(y_train_folds)[i]
        
        # [num_of_folds, num_in_flods, feature_of_x] -> [num_of_pictures, feature_of_x]
        Xtr = np.reshape(Xtr, (X_train.shape[0] * 4 / 5, -1))
        ytr = np.reshape(ytr, (y_train.shape[0] * 4 / 5, -1))
        Xte = np.reshape(Xte, (X_train.shape[0] / 5, -1))
        yte = np.reshape(yte, (y_train.shape[0] / 5, -1))
        
        classifier.train(Xtr, ytr)
        yte_pred = classifier.predict(Xte, k)
        yte_pred = np.reshape(yte_pred, (yte_pred.shape[0], -1))

        accuracy = np.sum(yte_pred == yte, dtype=float)/len(yte)   # bool to int,我们需要显示指定为float
        k_to_accuracies[k][i] = accuracy
################################################################################
#                                 END OF YOUR CODE                             #
################################################################################

# Print out the computed accuracies
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print \'k = %d, accuracy = %f\' % (k, accuracy)

SVM支持向量机

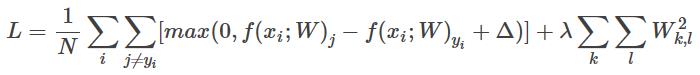
def svm_loss_vectorized(W, X, y, reg):
  """
  Structured SVM loss function, vectorized implementation.

  Inputs and outputs are the same as svm_loss_naive.
  """
  
  loss = 0.0
  dW = np.zeros(W.shape) # initialize the gradient as zero

  # 向前传播
  scores = X.dot(W)
  scores_correct = scores[np.arange(y.shape[0]),y].reshape(y.shape[0],1)
  margins = np.maximum(0., scores - scores_correct + 1)      # 错误类加上阈值减去正确类得分，满足的置零，不满足的计算loss
  margins[np.arange(y.shape[0]),y] = 0                       # 把上一步正确类参与计算的部分置零
  loss = np.sum(margins)/y.shape[0] + 0.5*reg*np.sum(W*W)

  # 反向传播
  margins[margins>0] = 1                         # 类relu反向传播
  row_grad = np.sum(margins, axis=1)
  margins[np.arange(y.shape[0]),y] - row_grad    # 分类器反向都是这样，错误类不动，正确类减去上层梯度
  dW = np.dot(X.T,margins)/y.shape[0] + reg*W

  return loss, dW