二叉树算法小结
Posted 凯帝农垦
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树算法小结相关的知识,希望对你有一定的参考价值。
概述
遍历二叉树有前序,中序,后序三大方法算。对于二叉树的三种不同的遍历方式,用递归的方法很容易写出实现代码,对于非递归的遍历算法使用数据结构堆栈作为工具代替递归以节省时空开销,在经过节点是先将其压入栈,要到他第几次从栈中弹出是才访问它,对于前序来说,是一次,对于中序来说是两次,对于后序则是三次。下面介绍下二叉树的几种遍历算法,包括递归和非递归的实现。
关于二叉树遍历方式的规则,可前往这里,本篇主要是对算法的陈列。
准备工作
首先,我们先建个二叉树结构
我们建立如下图所示的二叉树
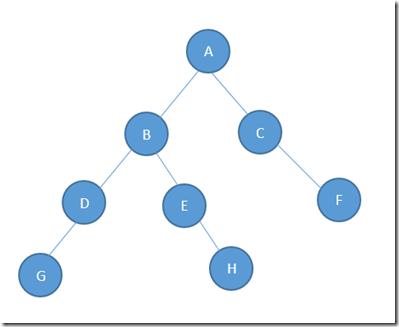
然后,我们创建树,和遍历的结构,采用策略模式,让客户端调用
//创建数的结构
public class Tree
{
public string Data { get; set; }
public Tree L_Tree { get; set; }
public Tree R_Tree { get; set; }
public Tree(string data)
{
this.Data = data;
this.L_Tree = null;
this.R_Tree = null;
}
public Tree(string data,Tree l,Tree r)
{
this.Data = data;
this.L_Tree = l;
this.R_Tree = r;
}
}
//定义一个管理树的类,
public class TreeManager
{
public TreeManager()
{
this.BuildTree();
}
//树的根节点
private Tree root_Tree;
private void BuildTree()
{
Tree g = new Tree("G");
Tree d = new Tree("D", g, null);
Tree h = new Tree("H");
Tree e = new Tree("E", null, h);
Tree b = new Tree("B", d, e);
Tree f = new Tree("F");
Tree c = new Tree("C", null, f);
Tree a = new Tree("A", b, c);
root_Tree = a;
}
//通过递归遍历
public void outputTree_Recursion(ITreeShow fs)
{
fs.show_Tree_Recursion(this.root_Tree);
}
//通过递归遍历
public void show_Tree_NonRecursion(ITreeShow fs)
{
fs.show_Tree_NonRecursion(this.root_Tree);
}
}
//定义了一个接口类 (作为先序,中序,后序等方式遍历的抽象)
public interface ITreeShow
{
void show_Tree_NonRecursion(Tree t);
void show_Tree_Recursion(Tree t);
}
准备工作做好以后,现在开始各种遍历算法的实现
先序遍历法
先序是根节点,左子树,右子数
//先序遍历
public class First_Read_Show : ITreeShow
{
//非递归-先序
public void show_Tree_NonRecursion(Tree t)
{
Stack<Tree> tree_stack = new Stack<Tree>();
while (t != null || tree_stack.Count > 0)
{
if (t != null)
{
Console.Write(t.Data+",");
tree_stack.Push(t);
t = t.L_Tree;
}
else
{
var item = tree_stack.Pop();
t = item.R_Tree;
}
}
}
//递归-先序
public void show_Tree_Recursion(Tree t)
{
if (t == null)
{
return;
}
Console.Write(t.Data + ",");
show_Tree_Recursion(t.L_Tree);
show_Tree_Recursion(t.R_Tree);
}
}
中序遍历法
中序是先左子树,再根节点,再右子树
public class Middle_Read_Show : ITreeShow
{
public void show_Tree_NonRecursion(Tree t)
{
Stack<Tree> stack_tree = new Stack<Tree>();
while (t != null || stack_tree.Count > 0)
{
if (t != null)
{
stack_tree.Push(t);
t = t.L_Tree;
}
else
{
var item = stack_tree.Pop();
Console.Write(item.Data+",");
t = item.R_Tree;
}
}
}
//递归-后序
public void show_Tree_Recursion(Tree t)
{
if (t == null)
{
return;
}
show_Tree_Recursion(t.L_Tree);
Console.Write(t.Data + ",");
show_Tree_Recursion(t.R_Tree);
}
}
后序遍历法
后序是先左子树,再右子树,再根节点
//后序遍历
public class Last_Read_Show : ITreeShow
{
//非递归-后序
public void show_Tree_NonRecursion(Tree t)
{
Stack<Tree> stack_tree = new Stack<Tree>();
HashSet<Tree> visited = new HashSet<Tree>();
while (t != null || stack_tree.Count > 0)
{
if (t != null)
{
stack_tree.Push(t);
t = t.L_Tree;
}
else
{
var item=stack_tree.Peek();
if (item.R_Tree != null && !visited.Contains(item.R_Tree))
{
t = item.R_Tree;
}
else {
Console.Write(item.Data+",");
visited.Add(item);
stack_tree.Pop();
}
}
}
}
//递归-后序
public void show_Tree_Recursion(Tree t)
{
if (t == null)
{
return;
}
show_Tree_Recursion(t.L_Tree);
show_Tree_Recursion(t.R_Tree);
Console.Write(t.Data + ",");
}
层次排序法
层序遍历就是按照层次由左向右输出
public class Layer_Read_Show : ITreeShow
{
public void show_Tree_NonRecursion(Tree t)
{
Queue<Tree> queue_tree = new Queue<Tree>();
if (t != null)
{
queue_tree.Enqueue(t);
while (queue_tree.Count > 0)
{
var item = queue_tree.Dequeue();
Console.Write(item.Data + ",");
if (item.L_Tree != null)
{
queue_tree.Enqueue(item.L_Tree);
}
if (item.R_Tree != null)
{
queue_tree.Enqueue(item.R_Tree);
}
}
}
}
public void show_Tree_Recursion(Tree t)
{
}
}
测试
static void Main(string[] args)
{
TreeManager tree = new TreeManager();
//先序-递归
Console.WriteLine("先序-递归:");
tree.outputTree_Recursion(new First_Read_Show());
//先序-非递归
Console.WriteLine();
Console.WriteLine("先序-非递归:");
tree.show_Tree_NonRecursion(new First_Read_Show());
//中序-递归
Console.WriteLine();
Console.WriteLine("中序-递归:");
tree.outputTree_Recursion(new Middle_Read_Show());
//中序-非递归
Console.WriteLine();
Console.WriteLine("中序-非递归:");
tree.show_Tree_NonRecursion(new Middle_Read_Show());
//后序-递归
Console.WriteLine();
Console.WriteLine("后序-递归:");
tree.outputTree_Recursion(new Last_Read_Show());
//后序-非递归
Console.WriteLine();
Console.WriteLine("后序-非递归:");
tree.show_Tree_NonRecursion(new Last_Read_Show());
//层次遍历
Console.WriteLine();
Console.WriteLine("层次遍历:");
tree.show_Tree_NonRecursion(new Layer_Read_Show());
Console.ReadKey();
}

总结
算法文字描述
二叉树的遍历算法包括递归和非递归两种,递归比较简单,先叙述下非递归算法的实现
为了便于理解,这里以下图的二叉树为例,分析二叉树的三种遍历方式的实现过程。
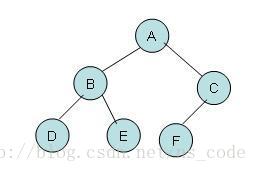
- 先序遍历的非递归实现
根据先序遍历的顺序,先访问根节点,再访问左子树,后访问右子树,而对于每个子树来说,又按照同样的访问顺序进行遍历,上图的先序遍历顺序为:ABDECF。非递归的实现思路如下:
对于任一节点P,- 输出节点P,然后将其入栈,再看P的左孩子是否为空;
- 若P的左孩子不为空,则置P的左孩子为当前节点,重复1)的操作;
- 若P的左孩子为空,则将栈顶节点出栈,但不输出,并将出栈节点的右孩子置为当前节点,看其是否为空;
- 若不为空,则循环至1)操作;
- 如果为空,则继续出栈,但不输出,同时将出栈节点的右孩子置为当前节点,看其是否为空,重复4)和5)操作;
- 直到当前节点P为NULL并且栈空,遍历结束。
- 中序遍历的非递归实现
根据中序遍历的顺序,先访问左子树,再访问根节点,后访问右子树,而对于每个子树来说,又按照同样的访问顺序进行遍历,上图的中序遍历顺序为:DBEAFC。非递归的实现思路如下:
对于任一节点P,- 若P的左孩子不为空,则将P入栈并将P的左孩子置为当前节点,然后再对当前节点进行相同的处理;
- 若P的左孩子为空,则输出P节点,而后将P的右孩子置为当前节点,看其是否为空;
- 若不为空,则重复1)和2)的操作;
- 若为空,则执行出栈操作,输出栈顶节点,并将出栈的节点的右孩子置为当前节点,看起是否为空,重复3)和4)的操作;
- 直到当前节点P为NULL并且栈为空,则遍历结束。
- 后序遍历的非递归实现
根据后序遍历的顺序,先访问左子树,再访问右子树,后访问根节点,而对于每个子树来说,又按照同样的访问顺序进行遍历,上图的后序遍历顺序为:DEBFCA。后序遍历的非递归的实现相对来说要难一些,要保证根节点在左子树和右子树被访问后才能访问,思路如下:
对于任一节点P,- 先将节点P入栈;
- 若P不存在左孩子和右孩子,或者P存在左孩子或右孩子,但左右孩子已经被输出,则可以直接输出节点P,并将其出栈,将出栈节点P标记为上一个输出的节点,再将此时的栈顶结点设为当前节点;
- 若不满足2)中的条件,则将P的右孩子和左孩子依次入栈,当前节点重新置为栈顶结点,之后重复操作2);
- 直到栈空,遍历结束。
完整代码下载地址:点这里
以上是关于二叉树算法小结的主要内容,如果未能解决你的问题,请参考以下文章