Uva 1103 古代象形符号（dfs求连通块， floodfill， 进制转换）

Posted 2020-09-28 Neord

题意：

给定一个H行W列的字符矩阵（H<200， W < 50）， 输入的是一个十六进制字符， 代表一行四个相邻的二进制， 1代表像素， 0代表没有像素。

然后要求判断输入的是以下哪些图形，注意图形可以伸缩变换， 但不能拉断。

 

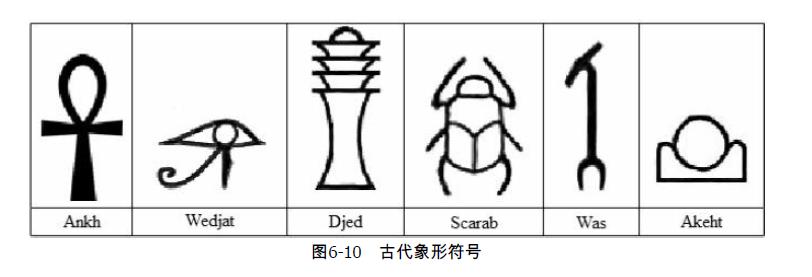
分析：

因为图形可以伸缩变换， 所以只要关注每个图形的特征， 

题目表中的6个符号从左到右依次有
1，3，5，4，0，2个白洞

我们先把十六进制还原成二进制建一幅图， 然后上下各留空一行， 左右各留空一列， 先把最外面的白色floodfill了（增加两行两列后保证外面的白色可以连成一块）， 然后再把整个图floodfill， 然后我们找黑色的区域（就是其中一个图形的边）， 看看他们与多少个白色区域相邻， 就可以依次对应图形了。

注意的是第5个图形， 一个像素点就可以看成第5个图形。

#include <bits/stdc++.h>
using namespace std;
#define rep(i,a) for(int i = 0; i < a; i++ )
string bin[256];
char G[250][70*4], tempG[250][70*4];
int vis[250][250];
int dx[] = {0,1,0,-1};
int dy[] = {1,0,-1,0};
char arc[8] = {0,\'W\',\'W\',\'A\',\'K\',\'J\',\'S\',\'D\'};
int H, W, cnt;
int dfs(int x, int y, int num){
    vis[x][y] = num;
    for(int i = 0; i < 4; i++){
        int tx = x + dx[i];
        int ty = y + dy[i];
        if(tx < 0 || tx >= H || ty < 0 || ty >= W || G[tx][ty] != G[x][y] || vis[tx][ty]!= 0)
            continue;
        dfs(tx,ty,num);
    }
}
int neighbor(int cnt){
    set<int> s;
    bool vis1[250][250];
    memset(vis1,0,sizeof(vis1));
    for(int i = 0; i < H; i++){
        for(int j = 0; j < W;j ++){
            if(vis[i][j] == cnt)
            for(int k = 0; k < 4; k++){
                int tx = i + dx[k];
                int ty = j + dy[k];
                if(tx < 0 || tx >= H || ty < 0 || ty >= W)
                    continue;
                if(!vis1[tx][ty]){
                    vis1[tx][ty] = 1;
                    s.insert(vis[tx][ty]);
                }
            }
        }
    }
    return (int)s.size();
}
int main(){
    bin[\'0\'] = "0000";bin[\'1\'] = "0001";bin[\'2\'] = "0010";bin[\'3\'] = "0011";bin[\'4\'] = "0100";bin[\'5\'] = "0101";bin[\'6\'] = "0110";bin[\'7\'] = "0111";
    bin[\'8\'] = "1000";bin[\'9\'] = "1001";bin[\'a\'] = "1010";bin[\'b\'] = "1011";bin[\'c\'] = "1100";bin[\'d\'] = "1101";bin[\'e\'] = "1110";bin[\'f\'] = "1111";
    int kase = 1;
    while(scanf("%d %d ", &H, &W) == 2 && H){
        for(int i = 0; i < 250;i++)
            fill(G[i],G[i]+280,\'0\');
        memset(tempG,0,sizeof(tempG));
        memset(vis,0,sizeof(vis));
        for(int i = 1; i <= H; i++){
            scanf("%s", tempG[i]);
            for(int j = 0; j< W;j++){
                for(int k = 0; k < 4; k++){
                    G[i][1+j*4+k] = bin[tempG[i][j]][k];
                }
            }
        }
        H += 2; W = W*4 +2; cnt = 1;
        vector<int> edge;
        for(int i = 0; i < H; i++){
            for(int j = 0; j < W; j++){
                  if(!vis[i][j]){
                       dfs(i,j,cnt);
                       if(G[i][j] == \'1\'){//如果是黑色
                            edge.push_back(cnt);
                       }
                       cnt++;
                  }
            }
        }
        printf("Case %d: ", kase++);
        string ans;
        for(int i = 0; i < edge.size();i++){
            ans+=arc[neighbor(edge[i])];
        }
        sort(ans.begin(), ans.end());
        for(int i = 0; i < ans.size(); i++)
            cout<< ans[i];
        puts("");
    }
}