算法竞赛之高精度以及部分组合的入门讲解

Posted 2020-09-28

    在算法竞赛之中，有时候一些题目的意思很容易就可以看出来解决步骤，但是数据却不是平常的数据量，而是高精度数据，这时候要是因为高精度的问题而使得这道题失去了AC的机会岂不是会被队友喷死，所以今天就教教大学关于高精度的一些算法吧。

    个人对于高精度的算法，感觉就是很原始的小时候学习加减乘除时候的做法。怎么说呢，当然是一位一位进行处理的，可能乘法有一些什么快速乘法的，这个等后面再进行讲解，现在就说说平常自己针对高精度是怎么进行处理的吧。

    首先呢，因为是高精度，那么数字的范围不大可能是int乃至__int64就可以存放的下来的，一般高精度的数字都是利用字符串直接进行存放的，所以我们的函数默认是传递两个字符串进来，对其进行相对应的操作，最后返回相对应的数据处理结果即可。

 

1. 高精度加法：

高精度加法的话，可能是整数与整数相加，也有可能是小数与小数进行运算，也出现不同号进行相加，当然在进行运算的时候，肯定是要判断两个数字的正负性，然后才会决定进行什么对应的操作，要是同号的话，那么就直接计算其绝对值的结果，然后加上相对应的符号。

我们先来介绍一下关于高精度加法之中的整数与整数进行加法运算吧，首先

就是先求出两个字符串的最长长度，然后在比较短的字符串前面给它默认填上相对应的字符串0，比如3210与123相加，最后的处理结果就是3210 + 0123，这样做的好处就是只要判断最首位运算之后，是否会进位即可。然后我们相对应的还要利用一个变量，判断当前的这步运算是否进位。是进行，则变量为1，若是不进位，则变量为0，同时变量参与下一步的运算之中。大概的步骤是如此，接下来我们举个例子吧：

1234567890000000000000000 + 99665433100000000000000000

那么处理之后的结果就是·

01234567890000000000000000

+ 99665433100000000000000000

--------------------------------

100900000990000000000000000

我们可以看的出来，是在进行7 + 3的时候产生了进位，这时候的变量就变为了1，那么之后进行的就是6 + 3 + 1 = 10，还是产生了进位，所以变量还是1，当前位%10的结果是0，所以当前位的结果位0，一直及逆行到2 + 6 + 1 = 9，没有产生进位，所以当前位的结果为9，下一步是9 + 1 = 10，所以当前位的结果位0，产生进位，首位的运算就是9 + 0 + 1 = 10，所以首位的结果是0，产生进位，所以单独输出1.最后的运算结果就是 100900000990000000000000000。

然后小数与小数进行高精度加法的时候，第一点就是将判断符号，然后将字符串根据小数点拆分成小数部分和整数部分，不存在的则用字符串"0"填充，然后利用上述的算法步骤进行计算，小数计算之后，是将后面补零，比如0.12 + 0.123变化为0.120 + 0.123，然后计算完小数之后则继续计算整数部分

代码：（整数 + 整数） 

 

#include <stdio.h> 
#include <string.h> 
 
char *strrev(char str[]){ 
     
    int len=strlen(str); 
    for(int i=0;i<len/2;i++){ 
        char ch=str[i]; 
        str[i]=str[len-i-1]; 
        str[len-i-1]=ch; 
    } 
    char *p=str; 
    return p; 
} 
 
int main(){ 
     
    char str[3][1005]={‘\\0‘}; 
    while(scanf("%s%s",str[0],str[1])==2){ 
        int len1=strlen(str[0]),len2=strlen(str[1]),len3=0; 
        int min=len1<len2?len1:len2,max=len1>len2?len1:len2,dex=0,num,t=0; 
        if(min!=len1) dex=1; 
        strcpy(str[0],strrev(str[0])),strcpy(str[1],strrev(str[1])); 
        for(int i=min;i<max;i++)    str[dex][i]=‘0‘; 
        for(int i=0;i<max;i++){ 
            num=str[0][i]-‘0‘+str[1][i]-‘0‘+t,t=0; 
            if(num>9) t=1; 
            str[2][len3++]=num%10+‘0‘; 
        } 
        if(t==1)    str[2][len3++]=‘1‘; 
        str[2][len3]=‘\\0‘; 
        strcpy(str[2],strrev(str[2])); 
        puts(str[2]); 
    }     
    return 0; 
} 

 

 

 

 

1. 高精度减法：

   这个的话，其实也是一步一步进行计算，不同点就是大减去小，所以在输之后，要先判断两个字符串所代表的数字，所以后者比前者大，那么就是后者减去前者，最后的计算结果加上"-"号即可，其他情况则不发生变化，都是前者减去后者。按照惯例，我们还是举一个例子，比如1 - 963245。

         和加法一样，要给它加上前补0，同时后者比前者大，所以在最后的结

果输出之前先输出负号，变化之后就是963245 - 000001.。

 

963245

• 000001

----------------

963244

所以最后的结果是-963244.因为过程和前面的加法类似，这里就不尽兴重复的说明了，直接给出代码： 

 

#include <stdio.h> 
#include <string.h> 
 
char *strrev(char str[]){ 
     
    int len=strlen(str); 
    for(int i=0;i<len/2;i++){ 
        char ch=str[i]; 
        str[i]=str[len-i-1]; 
        str[len-i-1]=ch; 
    } 
    char *p=str; 
    return p; 
} 
int main(){ 
     
    char str[3][1005]={‘\\0‘},temp[1005]; 
    while(scanf("%s%s",str[0],str[1])==2){ 
        bool ii=false; 
        int len1=strlen(str[0]),len2=strlen(str[1]),len3=0,max=len1>len2?len1:len2,min=len1+len2-max; 
        if(len1<len2||(len1==len2&&strcmp(str[0],str[1])<0)){ 
            ii=true; 
            strcpy(temp,str[0]),strcpy(str[0],str[1]),strcpy(str[1],temp); 
        } 
        strcpy(str[0],strrev(str[0])),strcpy(str[1],strrev(str[1])); 
        for(int i=min;i<max;i++) str[1][i]=‘0‘; 
        int num,t=0,i; 
        for(i=0;i<max;i++){ 
            num=str[0][i]-str[1][i]-t,t=0; 
            if(num<0) t=1; 
            str[2][len3++]=(num+10)%10+‘0‘; 
        } 
        str[2][len3]=‘\\0‘; 
        strcpy(str[2],strrev(str[2])); 
        if(ii==true) 
            printf("-"); 
        for(i=0;i<max;i++) 
            if(str[2][i]!=‘0‘)    break; 
        if(i==max) puts("0"); 
        strcpy(str[2],str[2]+i); 
        puts(str[2]); 
    } 
    return 0; 
} 

 

 

 

 

1. 感觉说了高精度加法之后，后面的步骤都是类似的，加减是一个道理，乘法其实也是一步一步来，只是在每次的计算之后，都要进行累加，举个简单的例子来直接计算运算，相信聪明的你应该很快就能明白了，重要的是，乘法里面的运算不会对输入的字符串进行处理，不过可以先预判是否有一个乘数为0，要是为0，就直接输出0就好了。

   365 x 632

        365

   X 632

   ----------

            730

   1095

2190

--------------

230680

怎么计算的，相信你应该知道，那么就是怎么利用代码实现呢，那就好好理解你的想法，可以将你要实现的步骤一步一步进行拆分，所有的大工程也都是基于一行一行的代码实现的，所以不要害怕，这里直接上代码： 

 

#include <stdio.h> 
#include <string.h> 
 
char *strrev(char str[]){ 
     
    int len=strlen(str); 
    for(int i=0;i<len/2;i++){ 
        char ch=str[i]; 
        str[i]=str[len-i-1]; 
        str[len-i-1]=ch; 
    } 
    char *p=str; 
    return p; 
} 
 
int main(){ 
     
    char str1[1005]={‘\\0‘},str2[1005]={‘\\0‘}; 
    while(scanf("%s",str1)==1){ 
        scanf("%s",str2); 
        int len1=strlen(str1),len2=strlen(str2); 
        if(strcmp(str1,"0")==0||strcmp(str2,"0")==0){ 
            puts("0"); 
            continue; 
        } 
        strcpy(str1,strrev(str1)),strcpy(str2,strrev(str2)); 
        int ans[2005],t=0,i,j; 
        for(i=0;i<len1+len2;i++)    ans[i]=0; 
        for(i=0;i<len1;i++) 
            for(j=0;j<len2;j++) 
                ans[i+j]+=(str1[i]-‘0‘)*(str2[j]-‘0‘); 
        for(i=0;i<len1+len2;i++){ 
            ans[i]=ans[i]+t; 
            t=ans[i]/10,ans[i]=ans[i]%10; 
        } 
        for(i=len2+len1-1;i>=0;i--) 
            if(ans[i]!=0) 
                break;     
        for(int j=i;j>=0;j--) 
            printf("%d",ans[j]); 
        printf("\\n"); 
    } 
    return 0; 
} 
 

 

 

 

 

说完了基本的高精度运算之后，为什么不说除法和取模呢？主要感觉除法是真的烦，而且感觉你们可能也没有时间去学习这个，要是想了解的话，到时候看群里的人要是比较多人在掌握了加减乘法以及下面说到的高精度组合之后，还想继续了解的话，那么到时候会再花点时间讲解一下高精度的除法和取模，不过估计还是以思路为主吧，比较想起来还是会用到乘法和减法吧，也是烦的可以。

组合数学的话，这里就介绍几个我感觉会比较经常出现的吧，一般是要了解，而且这个玩意是一个基础。嗯，你可以看作是四则运算那样子，有时候虽然算是考到了，然而其实还是考这个概念，个人愚见。

下面谈谈杨辉三角吧，这个算是组合算法的一种吧。

下面就来画一下杨辉三角这个东西

1

1. 1

1 2 1

1 3 3 1

1 4 6 4 1

1. 5 10 10 5 1
2. 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

1. 9 36 84 126 126 68 36 9 1

………………………………………………………………………………..

这是一个简化版本的杨辉三角，什么是杨辉三角呢，就是一个三角形的最左和最右都是1，然后若是按照数组的概念的解释的话，我们这里以1为起始，那么就是arr[n][1] = arr[n][n] = 1;

arr[i][j] = arr[i-1][j-1] + arr[i-1][j] (I > 2 && j < i)

然后就是再n的时候，就需要高精度加法来实现了，当n超过一百的时候，肯定就是利用高精度进行实现了，这个部分自己可以试着去实现。

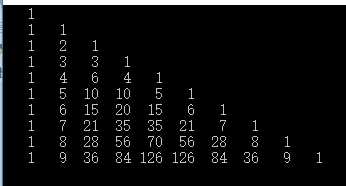
代码实现：

#include <stdio.h> 
#include <string.h> 
 
int main() { 
     
    int arr[25][25]; 
    memset(arr, 1, sizeof(arr)); 
    arr[0][0] = 1; 
    printf(" 1\\n"); 
    for(int i=1; i<10; i++) { 
        arr[i][0] = arr[i][i] = 1; 
        printf("%4d", arr[i][0]); 
        for(int j=1; j<i; j++) { 
            arr[i][j] = arr[i-1][j-1] + arr[i-1][j]; 
            printf("%4d", arr[i][j]); 
        } 
        printf("%4d\\n", arr[i][i]); 
    } 
    return 0; 
} 

 

 

下面说说全排列这个问题，正常的去全排列是利用搜索去处理的，不过搜索处理的全排列数据范围也不能超过20好像，这里介绍的是两个公式，即康拓展开和逆康拓展开

下面直接介绍一下根据全排列的结果判断这是第几个全排列，举个例子，由{1,2,3}组成的全排列之中，321是第几个，按照正常的话，我们肯定会去写个搜索跑一下，虽然很快就出来了答案，那是因为数据比较少，而且要是手边正好没有电脑，就会比较麻烦，所以我们这里就介绍一下，利用纸笔就可以直接算出的方法

首先分析一下：

第一位是3，小于3的数有1、2 。所以有2*2!个。再看小于第二位，小于2的数只有一个就是1 ，所以有1*1!=1 所以小于32的{1,2,3}排列数有2*2!+1*1!=5个。所以321是第6个大的数。2*2!+1*1!是康托展开

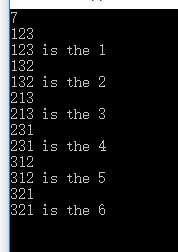
这样子看起来，是不是就简单很多了，下面给出代码实现：

#include <stdio.h> 
#include <string.h> 
 
using namespace std; 
 
int main() { 
     
    int num[5] = {1, 2, 3}; 
    bool vis[5]; 
    int t; 
    int a[5] = {2, 1, 1}; 
    scanf("%d ", &t); 
    while(t--) { 
        char str[6] = {‘\\0‘}; 
        gets(str); 
        memset(vis, false, sizeof(vis)); 
        vis[0] = true; 
        int ans = 1; 
        for(int i = 0; i < 3; i++) { 
            int t = 0; 
            for(int j = 0; j < str[i] - ‘0‘; j++) 
                if(vis[j] == false) 
                    t++; 
            ans += t * a[i]; 
            vis[str[i] - ‘0‘] = true; 
        } 
        printf("%s is the %d\\n", str, ans); 
    } 
    return 0; 
} 

 

下面说说怎么根据第n个求出对应的数组

还是以{1, 2, 3}为基本组成元素

比如查找第4个元素，那么我们要先将4减去1，因为求出来的第0个元素和我们认为的第一个是同一个，所以要先自减。

3去除 2!,得到的是1，余1；说明前面有1个比它小，所以当前{1, 2, 3},第二小2

1去除 1!,的带的是1，余0；说明前面有0个比它小，所以当前{1，3}最小0

0去除 1!,的带的是0，余0；剩余最后一个数字3.

所以得到的是213

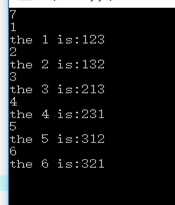
代码实现：

#include <stdio.h> 
#include <string.h> 
 
using namespace std; 
 
int main() { 
     
    int num[5] = {1, 2, 3}; 
    bool vis[5]; 
    int t; 
    int a[5] = {2, 1, 1}; 
    scanf("%d", &t); 
    while(t--) { 
        int cnt; 
        scanf("%d", &cnt); 
        printf("the %d is:", cnt); 
        cnt--; 
        memset(vis, false, sizeof(vis)); 
        for(int i = 0; i < 3; i++) { 
            int size = cnt / a[i]; 
            cnt = cnt % a[i]; 
            int j = 0, in = 0; 
            while(j < size) { 
                if(vis[in] == false) 
                    j++; 
                in++; 
            } 
            while(vis[in] == true) 
                in++; 
            vis[in] = true; 
            printf("%d", num[in]); 
        } 
        printf("\\n"); 
    } 
    return 0; 
} 

 

 

至于其他的高精度算法的话，就之后再进行讲解吧，希望这个博客对大家关于高精度以及排列组合的一些算法的理解有帮助