神奇的位运算

Posted 2020-09-28 云开的立夏

位运算的威力

前言：

在学习Java二进制各种转换时，发现对位运算很不熟悉，怪我基础没打好，更要好好学习了。然后从网上搜刮了一些位运算的小应用，然后有一些不熟悉的自己用Java代码试了一下，发现真的很神奇，习惯了用普通的运算方法，对位运算一时半会还真的不习惯，看着式子也要思考一会才能想通，不过掌握了位运算对计算效率真的有很大的提升，大家不妨来看一下。

参考博文：http://blog.csdn.net/iukey/article/details/7195265

---

对于基本的位运算操作符，我在上一篇已经讲解过了，不清楚的朋友请转移到：http://www.cnblogs.com/hysum/p/7190388.html

对于基本的运算操作符有一个口诀献给大家：

清零取数要用与，某位置一可用或

若要取反和交换，轻轻松松用异或

---

 下面来看几个具体的例子：

1) 判断int型变量a是奇数还是偶数          

a&1 = 0 偶数

a&1 = 1 奇数

1 //判断int型变量a是奇数还是偶数
2         System.out.println("请输入一个整数：");
3         Scanner in=new Scanner(System.in);
4         int a=in.nextInt();
5         if((a&1)==0) 
6             System.out.println("您输入的是偶数！");
7         if((a&1)==1)
8             System.out.println("您输入的是奇数！");
9 System.out.println("您输入的数二进制为："+Integer.toBinaryString(a));

运行结果：

2) 取int型变量a的第k位 (k=0,1,2……sizeof(int))，即a>>k&1   (先右移再与1)

3) 将int型变量a的第k位清0，即a=a&~(1<<k)（1左移取反再与a）

4) 将int型变量a的第k位置1，即a=a|(1<<k)  （1左移或上a）

以上三个例子：

 1 System.out.println("请输入一个整数：");
 2         Scanner in=new Scanner(System.in);
 3         int a=in.nextInt(); 5         System.out.println("您输入的数二进制为："+Integer.toBinaryString(a));
 6         System.out.println("取int型变量a的第2位："+(a>>1&1));    
 7         a=a&~(1<<2);//将int型变量a的第3位清0
 8         System.out.println("将第3位清0后的二进制为："+Integer.toBinaryString(a));
 9         a=a|(1<<2);//将int型变量a的第3位置1
10         System.out.println("将第3位置1后的二进制为："+Integer.toBinaryString(a));

运行结果：

7)对于一个数 x >= 0，判断是不是2的幂。

1 boolean power2(int x){return ( (x&(x-1))==0) && (x!=0);}

8)不用temp交换两个整数

1 public void swap(int x , int y)
2 {x ^= y;y ^= x;x ^= y;}

9)计算绝对值

1         //计算绝对值
2         int y ;
3         y = a >> 31;
4         System.out.println(y);  
5         System.out.println("绝对值为："+ ((a^y)-y));  //or: (a+y)^y
6         

运行结果:

 

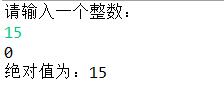
分析：可以看出y的值由a来决定，当a为正数y等于0，当a为负数y等于-1。知道了y的值的含义，那么接下来计算绝对值的式子就不难理解了，对于正数来说两个式子都是a^0等于a本身；对于负数来说，第一个式子(a^y)-y，可以看成先取反然后加上1（相当于原码转为补码）；第二个式子(a+y)^y，可以看成先减1然后取反（相当于补码转为原码）。因为原码和补码是相对的，所以两个式子的计算结果是一样的。

10)取模运算转化成位运算 (在不产生溢出的情况下，正数)

a % (2^n) 等价于 a & (2^n - 1)

a % 2 等价于 a & 1   

11)乘法运算转化成位运算 (在不产生溢出的情况下，正数)

a * (2^n) 等价于 a<< n

乘除2的倍数：千万不要用乘除法，非常拖效率。只要知道左移1位就是乘以2，右移1位就是除以2就行了。比如要算25 * 4，用25 << 2就好啦

12)除法运算转化成位运算 (在不产生溢出的情况下，正数)

a / (2^n) 等价于 a>> n

与乘法上述同理。

13) if (x == a) x= b else  x= a;

　　等价于 x= a ^ b ^ x;

14) x 的 相反数 表示为 (~x+1)

---

再来看两个具体的应用，更深入理解位运算：

例1.子网掩码

本人的网络没怎么学，对于子网掩码也是了解个大概，具体内容可以自己去google，等博主学好了会给大家分享相关内容的。下一篇博文：《了解网络之子网掩码详解》

假如我是一个网管，公司内部使用C类地址，现在我要把公司网络划分成5个子网，网络号为192.168.1.0的前三段，那么子掩码怎么填呢？

子网的子网掩码：192.168.1.224。(当然这里还有其他答案，我取的是在子网扩充不超过6个的情况下的每个子网所容纳主机最多的最佳方案)。

这个怎么来的呢？

ip本身是个二进制位的，为了方便人们设置，我们采用了点分十进制的转换，把32位的ip地址转换成了4个字节的十进制莱表示。比如 192.168.1.213 这个ip地址的二进制表示为：11000000 10101000 00000001 11010101 。对于C类地址默认的前三个字节表示网络号，那么这个网络号就是：11000000 10101000 00000001，最后一个字节11010101表示主机号，可以知道这个网络可以容纳的最多主机数为2^8-2，为什么减2？因为主机号全为0的是网络地址,不可用，主机号全为1的是广播地址,也不可以分配给主机，所以要减去网络地址和广播地址，也就是减去2了。现在要划分子网，那么我们就要从表示主机的那个字节也就是8个位里面拿出几个位来表示子网号， 几位比较合适呢？这就要看你需要划分多少个子网咯。比如我们现在要划分5个子网，(5)10 = (101)2 ，那么至少就需要3位了，而且最多可以划分2^3-2 = 6个子网，这里减2的道理与主机相同。现在把224换成二进制看看吧(224)10 = (11100000)2  ,明白了吧，我们可以推断出子网掩码干了什么勾当？不错子网掩码与ip地址做了按位与运算，他的作用就是屏蔽了主机号获取网络号与子网号。

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

例2. 防止int型变量溢出(C/C++)

1  int x = 32760;int y = 32762; 要求求x、y的平均值。
2 int ave(int x, int y)   //返回X、Y的平均值
3 {   
4      return (x & y) + ( (x^y)>>1 );
5 }

知识点：

>>n 相当于除于2^n ，<<n 相当于乘于2^n .

 x,y对应位均为1，相加后再除以2还是原来的数，如两个00001000相加后除以2仍得00001000,那么我们把x与y分别分成两个部分来看,两者相同的位分别拿出来 则 :

x = (111111111111000)2 =  (111111111111000)2 +  (000000000000000)2

y =  (111111111111010)2 =  (111111111111000)2 +  (000000000000010)2

相同部分我们叫做x1,y1,不同部分我们叫做x2,y2.那么现在(x+y)/2 =(x1+y1)/2 +(x2 + y2)/2 ,因为x1 == y1 ,所以(x1+y1)/2 ==x1 ==y1,相同部分我们用与运算求出来 x1 = x&y ,不同部分的和我们用^求出来,然后除于2是不是我们想要的结果了呢？   

为什么要用位运算来求解呢？为了防止int型变量溢出！

我们都知道int型是有范围的，它是一个32bit的整数类型，平常我们计算小的数据的平均数不需要用位运算，但是如果你要计算的数据你自己无法估计，但是只知道要计算的两个数都是在int范围里的，如果我们用常规的方法计算这两个数，它们的和超过了int的范围则就会发生溢出。这里用位运算就很好地避免了这个问题，因为在这个算法中用&运算来获取两个数相同的部分，相同的部分不需要再相加，用^运算来获取俩者的不同的部分的1再除以2。通过二进制的形式很容易发现，这样的做法是不会发生溢出的。保证了算法的可靠性。

这个例子有点难于理解.但是经过我的分解应该还算好理解了，弄懂这个例子相信你的位运算已经登入大门了。

---

下面我将网络上找到的位运算的各种应用例子整理成了一个表格，供大家参考：

功能	示例	位运算
去掉最后一位	(101101->10110)	x >> 1
在最后加一个0	(101101->1011010)	x < < 1
在最后加一个1	(101101->1011011)	x < < 1+1
把最后一位变成0	(101101->101100)	x | 1-1
最后一位取反	(101101->101100)	x ^ 1
把右数第k位变成1	(101001->101101,k=3)	x | (1 < < (k-1))
把右数第k位变成0	(101101->101001,k=3)	x & ~ (1 < < (k-1))
右数第k位取反	(101001->101101,k=3)	x ^ (1 < < (k-1))
取末三位	(1101101->101)	x & 7
取右数第k位	(1101101->1,k=4)	x >> (k-1) & 1
把末k位变成1	(101001->101111,k=4)	x | (1 < < k-1)
末k位取反	(101001->100110,k=4)	x ^ (1 < < k-1)
把右边连续的1变成0	(100101111->100100000)	x & (x+1)
把右起第一个0变成1	(100101111->100111111)	x | (x+1)
把右边连续的0变成1	(11011000->11011111)	x | (x-1)
取右边连续的1	(100101111->1111)	(x ^ (x+1)) >> 1
去掉右起第一个1的左边	(100101000->1000)	x & (x ^ (x-1))

---

结束语：想问问各位大佬，位运算在哪里应用的最多？是不是C/C++这种面向底层的语言更多接触到位运算？了解颇浅，希望能有个解答，谢谢！！