压缩[SCOI2007]

Posted 2020-09-28 moyiii

题目描述  给一个由小写字母组成的字符串，我们可以用一种简单的方法来压缩其中的重复信息。压缩后的字符串除了小写字母外还可以（但不必）包含大写字母R与M，其中M标记重复串的开始，R重复从上一个M（如果当前位置左边没有M，则从串的开始算起）开始的解压结果（称为缓冲串）。 bcdcdcdcd可以压缩为bMcdRR，下面是解压缩的过程

             

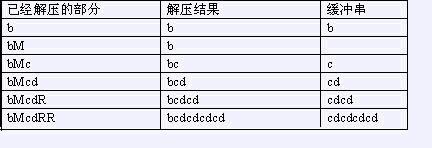
  另一个例子是abcabcdabcabcdxyxyz可以被压缩为abcRdRMxyRz。

输入

输入仅一行，包含待压缩字符串，仅包含小写字母，长度为n。

输出

输出仅一行，即压缩后字符串的最短长度。

样例输入

bcdcdcdcdxcdcdcdcd

样例输出

12
  

题解   把题目读懂就挺不容易的。。。考试的时候读了很久的题，很久没做过区间dp，没想到正解。大致写了一下每一位的值可以怎么得到，就被循环节给绕进去了。因为没有细致做这道题，样例也没有手动分析。下午改题之前动手模拟了一个测试点，就对“重复”这个定义的理解深了很多。
         f[i][j]表示i之前有一个重复开始，到j的最小长度。
         f[i][i]=2;在i之前放置起点
         bj(f[i][j],f[i][j-1]+1);确认之前更新的是否最优
         bj(f[i][j*2-i+1],f[i][j]+1);如果循环在继续，以i到j为一个循环节更新下一个循环节
         f[i][i]=1;起点本身没必要循环
         之后再类似弗洛伊德确认各区间最优值bj(f[i][j],f[i][k]+f[k+1][j]);
         结果即为f[0][n-1];
    关于dp还是要有更抽象的概念，如果纠结于细节就会越绕越深。要善于抓住问题的关键，列出状态，否则真是没办法做。对于和字符串有关的题一直觉得难做，其实也是因为不擅长把字符转化成数之间的关系。只要找准状态，严格按照状态设计程序，dp应该是有规律可循的。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
int n,f[55][55];
string a;
bool d;
void bj(int &x,int y)
{
     x=x<y?x:y;
}
int main()
{
    freopen("compress.in","r",stdin);
    freopen("compress.out","w",stdout);
    memset(f,0x3f,sizeof(f));
    cin>>a;
    n=a.size();
    for(int i=0;i<n;i++)
    {
       f[i][i]=2;
       if(i==0)  f[i][i]=1;
       for(int j=i+1;j<n;j++)
       {
          bj(f[i][j],f[i][j-1]+1);
          if(j*2-i+1<n)
          {
            d=1;
            for(int k=0;k<=j-i;k++)
              if(a[i+k]!=a[j+k+1])
              {
                 d=0;
                 break;
              }
            if(d)
              bj(f[i][j*2-i+1],f[i][j]+1);
          }
       }
       f[i][i]=1;
    }
    for(int i=0;i<n;i++)
      for(int j=i;j<n;j++)
        for(int k=i;k<=j;k++)
          bj(f[i][j],f[i][k]+f[k+1][j]);
    printf("%d",f[0][n-1]);
    //while(1);
    return 0;
}