历年NOIP中的搜索题
Posted Fenghr
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了历年NOIP中的搜索题相关的知识,希望对你有一定的参考价值。
什么题目都不会做于是开始做搜索题。
然而我搜索题也不会做了。
铁定没戏的蒟蒻。
1.NOIP2004 虫食算
“对于给定的N进制加法算式,求出N个不同的字母分别代表的数字,使得该加法算式成立。输入数据保证有且仅有一组解”。
大概就是给你一堆(n个)字母让你求出n进制下的一个n位数加n位数得到n位数的唯一解(允许有前导0)。
千算万算没算到最大的优化是从大到小枚举数字
反正顶多26位,个位开始爆搜2333。
几个比较重要的剪枝:
当前列不可能满足立即退出。
一列三个数,知二推一。
当前答案与之前冲突立即退出。
然后枚举的时候从n枚举到1。
过了。
可能写得稍微那么丑了一点?
#include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <vector> #include <cstring> #include <queue> #include <complex> #include <stack> #define LL long long int #define rg register #define ls (x << 1) #define rs (x << 1 | 1) #define MID int mid=(l+r)>>1 using namespace std; const int N = 110; int fac[N],In[N],n,D[N]; char A[N],B[N],C[N]; int gi() { int x=0,res=1;char ch=getchar(); while(ch>\'9\'||ch<\'0\'){if(ch==\'-\')res*=-1;ch=getchar();} while(ch<=\'9\'&&ch>=\'0\')x=x*10+ch-48,ch=getchar(); return x*res; } inline char gc() { char ch=getchar(); while(ch>\'Z\' || ch<\'A\')ch=getchar(); return ch; } inline int F(rg char ch){return int(ch-\'A\'+1);} inline void Congratulations() { for(rg int i=1;i<=n;++i) printf("%d ",fac[i]); exit(0); } inline void dfs(rg int dep,rg int line) { if(line==1){ rg char ch=A[dep];rg int f=F(ch); if(fac[f]!=-1)dfs(dep,2); else for(rg int i=n-1;i>=0;--i) if(!In[i]){ fac[f]=i;In[i]=1; dfs(dep,2); fac[f]=-1;In[i]=0; } return; } else if(line==2){ rg char ch=B[dep];rg int f=F(ch); if(fac[f]!=-1)dfs(dep,3); else{ rg int f1=F(A[dep]),f3=F(C[dep]); rg int sum=fac[f1]+D[dep]; if(fac[f3]!=-1){ int x=fac[f3]-sum; while(x<0)x=x+n; if(!In[x]){ fac[f]=x;In[x]=1; dfs(dep,3); fac[f]=-1;In[x]=0; } } else for(rg int i=n-1;i>=0;--i) if(!In[i]){ fac[f]=i;In[i]=1; dfs(dep,3); fac[f]=-1;In[i]=0; } } return; } else{ rg char ch=C[dep];rg int f=F(ch); rg int sum=fac[F(A[dep])]+fac[F(B[dep])]+D[dep],ssum=sum-n; if(fac[f]!=-1){ if(fac[f]!=sum && fac[f]!=ssum)return; else{ if(sum>=n && dep==1)return; if(dep==1)Congratulations(); D[dep-1]=sum>=n;dfs(dep-1,1); } } else{ if(sum>=n){ if(dep==1)return; if(!In[ssum]){ D[dep-1]=1; fac[f]=ssum; In[ssum]=1; dfs(dep-1,1); In[ssum]=0; fac[f]=-1; } else return; } else{ if(!In[sum]){ if(dep==0)Congratulations(); D[dep-1]=0;fac[f]=sum;In[sum]=1; dfs(dep-1,1); In[sum]=0;fac[f]=-1; } else return; } } } } inline void work() { for(rg int i=1;i<=n;++i)fac[i]=-1; dfs(n,1); } int main() { n=gi(); for(int i=1;i<=n;++i)A[i]=gc(); for(int i=1;i<=n;++i)B[i]=gc(); for(int i=1;i<=n;++i)C[i]=gc(); work(); return 0; }
2.NOIP2009靶形数独
一个数独每个方格都有一定的权Ai,j,给你一个不完全的数独,定义数独分数为所有方格的(方格内数和该方格权的积)的和,求分数最大的数独,无解输出-1。
第一次打,直接从(1,1)枚举到(9,9),爆搜2333。
90分。
一笋干就来了兴趣,然后(观察了一下数据)发现答案集中在其他三个角的时候跑的贼吉八慢。
把角落上的点的个数划分个区域统计一下,从那个点开始爆搜。
于是过了。
不科学啊,复杂度是应该很高的啊... ...
反正大力出奇迹嘛。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <complex>
#include <stack>
#define LL long long int
#define ls (x << 1)
#define rs (x << 1 | 1)
#define MID int mid=(l+r)>>1
using namespace std;
int map[21][21],bel[11][21][21],vis[21][21];
int In[21][21],In_1[21][21],In_2[21][21];
int point[]={0,6,7,8,9,10},Ans,f1,f2,f3,f4,fuc[21][21];
int gi()
{
int x=0,res=1;char ch=getchar();
while(ch>\'9\'||ch<\'0\'){if(ch==\'-\')res*=-1;ch=getchar();}
while(ch<=\'9\'&&ch>=\'0\')x=x*10+ch-48,ch=getchar();
return x*res;
}
inline void TS()
{
for(int i=1;i<=9;++i){
for(int j=1;j<=9;++j)
printf("%d ",vis[i][j]);
printf("\\n");
}
}
inline void dfs(int x,int y,int nf,int tc,int kind)
{
if(tc>=81){Ans=max(Ans,nf);return;}
if(x<1 || y<1 || x>9 || y>9)return;
if(map[x][y]){
vis[x][y]=map[x][y];
nf+=point[bel[2][x][y]]*map[x][y];
if(kind==1){
if(y==9)dfs(x+1,1,nf,tc+1,kind);
else dfs(x,y+1,nf,tc+1,kind);
}
else if(kind==2){
if(y==1)dfs(x+1,9,nf,tc+1,kind);
else dfs(x,y-1,nf,tc+1,kind);
}
else if(kind==3){
if(y==9)dfs(x-1,1,nf,tc+1,kind);
else dfs(x,y+1,nf,tc+1,kind);
}
else if(kind==4){
if(y==1)dfs(x-1,9,nf,tc+1,kind);
else dfs(x,y-1,nf,tc+1,kind);
}
return;
}
int Bel=bel[1][x][y],pt=point[bel[2][x][y]];
for(int i=9;i;--i){
if(!In[Bel][i])
if(!In_1[x][i])
if(!In_2[y][i]){
vis[x][y]=i;
In[Bel][i]=1;
In_1[x][i]=1;
In_2[y][i]=1;
int fn=nf+pt*i;
if(kind==1){
if(y==9)dfs(x+1,1,fn,tc+1,kind);
else dfs(x,y+1,fn,tc+1,kind);
}
else if(kind==2){
if(y==1)dfs(x+1,9,fn,tc+1,kind);
else dfs(x,y-1,fn,tc+1,kind);
}
else if(kind==3){
if(y==9)dfs(x-1,1,fn,tc+1,kind);
else dfs(x,y+1,fn,tc+1,kind);
}
else if(kind==4){
if(y==1)dfs(x-1,9,fn,tc+1,kind);
else dfs(x,y-1,fn,tc+1,kind);
}
vis[x][y]=0;
In[Bel][i]=0;
In_1[x][i]=0;
In_2[y][i]=0;
}
}
}
int main()
{
for(int i=1;i<=9;++i)
for(int j=1;j<=9;++j)
map[i][j]=gi();
for(int i=1;i<=9;++i)
for(int j=1;j<=9;++j){
bel[1][i][j]=((i-1)/3)*3+((j-1)/3)+1;
bel[2][i][j]=min(min(i,j),min(9-i+1,9-j+1));
}
for(int i=1;i<=9;++i)
for(int j=1;j<=9;++j)
if(map[i][j]){
In[bel[1][i][j]][map[i][j]]=1;
In_1[i][map[i][j]]=1;
In_2[j][map[i][j]]=1;
}
for(int i=1;i<=9;++i)
for(int j=1;j<=9;++j)
if(map[i][j]){
if(i<=5 && j<=5)f1++;
if(i<=5 && j>=5)f2++;
if(i>=5 && j<=5)f3++;
if(i>=5 && j>=5)f4++;
}
if(f1>=f2 && f1>=f3 && f1>=f4)dfs(1,1,0,0,1);
else if(f2>=f1 && f2>=f3 && f2>=f4)dfs(1,9,0,0,2);
else if(f3>=f1 && f3>=f2 && f3>=f4)dfs(9,1,0,0,3);
else dfs(9,9,0,0,4);
printf("%d\\n",Ans?Ans:-1);
return 0;
}
3.NOIP2010引水入城
一个矩形地带,每个格子有高度。
最上面一行可以建蓄水厂,中间的可以建输水站。
水只能从高处流向低处(平地不行),只能从一个点流向有公共边的点。
问最少要几个蓄水厂才能使最后一行的城市都有水。无解输出-1。
矩形最大是500×500的。
首先很容易想到只在第一行的比左右都高的点修就可以了啊。
然后把这些点爆搜一遍看它能走到的最左边和最右边。
容易证明一个点能走到的一定是一条连续的线段,如果不是就可以-1了。
然后就是很经典的线段覆盖区间问题。
贪心和DP都可以。我也搞不清是什么方法。
处理这些线段先按左端点排序,然后开一个队列,从左往右扫一遍。
如果当前线段覆盖了上一条线段的"有用区间"(即相对上上个线段外的区间),就把上一个区间从队列里去掉。
直到去不掉了就把这条线段加在队列里。
如果被上一条覆盖了,直接跳过算了。
如果没覆盖,就把这个线段加进队列,进行下一波计算。
把细节卡好就差不多了,也不是什么很难的题。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <complex>
#include <stack>
#define LL long long int
#define rg register
using namespace std;
const int N = 510;
const int Inf = 1e6+7;
int n,m,high[N][N],L[N][N],R[N][N],Left[N],Right[N];
int st,ed=1,que[N],vis[N][N];
int gx[]={0,1,-1,0,0},gy[]={0,0,0,1,-1};
inline int gi()
{
rg int x=0,res=1;rg char ch=getchar();
while(ch>\'9\'||ch<\'0\'){if(ch==\'-\')res*=-1;ch=getchar();}
while(ch<=\'9\'&&ch>=\'0\')x=x*10+ch-48,ch=getchar();
return x*res;
}
inline bool check(rg int x,rg int y,rg int h)
{
if(x<1 || y<1 || x>n || y>m)return false;
return h>high[x][y];
}
inline void dfs(rg int bel,rg int x,rg int y)
{
if(L[x][y]!=m+1 && R[x][y]!=-1){
Left[bel]=min(Left[bel],L[x][y]);
Right[bel]=max(Right[bel],R[x][y]);
return;
}
if(vis[x][y])return;vis[x][y]=1;
for(int i=1;i<=4;++i)
if(check(x+gx[i],y+gy[i],high[x][y])){
dfs(bel,x+gx[i],y+gy[i]);
L[x][y]=min(L[x][y],L[x+gx[i]][y+gy[i]]);
R[x][y]=max(R[x][y],R[x+gx[i]][y+gy[i]]);
}
if(x==n){
L[x][y]=min(y,L[x][y]!=m+1?L[x][y]:y);
R[x][y]=max(y,R[x][y]!=0-1?R[x][y]:y);
}
Left[bel]=min(Left[bel]?Left[bel]:L[x][y],L[x][y]);
Right[bel]=max(Right[bel]?Right[bel]:R[x][y],R[x][y]);
return;
}
int main()
{
n=gi();m=gi();
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j){
L[i][j]=m+1;R[i][j]=-1;
high[i][j]=gi();
}
high[n][0]=high[n][m+1]=-Inf;
for(int i=1;i<=m;++i)
Left[i]=m+1,Right[i]=-1,dfs(i,1,i);
for(int i=1;i<=m;++i)
if(L[n][i]>R[n][i])st++;
if(st){printf("0\\n%d\\n",st);return 0;}
st=1;ed=0;
for(int i=1,last=1;i<=m;){
if(high[1][i]<high[1][i+1]){++i;continue;}
if(high[1][i]<high[1][i-1]){++i;continue;}
if(Left[i]>Right[i]){++i;continue;}
if(ed==0){
que[++ed]=i;
last=1;
++i;
continue;
}
if(Left[i]<=last && Right[i]>=Right[que[ed]]){
ed--;
if(ed>1)last=Right[ed-1]+1;
else last=1;
continue;
}
else if(Left[i]>last){
if(Right[i]>Right[que[ed]]){
last=Right[que[ed]]+1;
que[++ed]=i;
}
++i;
}
}
printf("1\\n%d\\n",ed);
return 0;
}
4.NOIP2013华容道
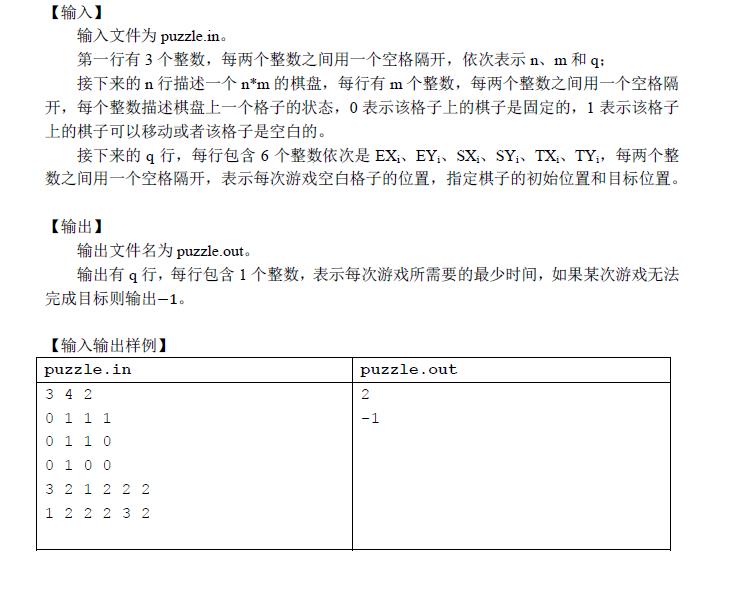
给你一个华容道图,里面的小格子都是1×1的,有些小格子可以移动,有一个空格。
每一次移动操作需要的时间为1,问把一个指定块移到一个指定区域的最小时间。
Q次询问。矩形最大是30*30,Q最大是500

大概花了个二十分钟就写了个能鬼到65的BFS。有人说优化一下状态可以搞到80。
然后开始想正解,发现完全没什么戏。于是去%了一下,经过一番鄙视和提点之后开始了漫长的征途。
首先预处理出,从一个点的上下左右到上下左右,不经过这个点的最短路。
可以固定住这个点,视为不可移动状态,然后处理。
然后把空格移到起始点,然后把起始点移到终点。
用SPFA维护,大概要开三维状态,(x,y)和方向(上下左右)。
OI界的毒瘤一颗。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <complex>
#include <stack>
#define LL long long int
#define ls (x << 1)
#define rs (x << 1 | 1)
#define MID int mid=(l+r)>>1
using namespace std;
const int N = 31;
struct Data{int x,y,from;};
struct Dot{int x,y;};
int n,m,Q,map[N][N],Ex,Ey,Sx,Sy,Tx,Ty;
int Gx[]={0,0,1,0,-1},Gy[]={0,1,0,-1,0};
int far[N][N][5][5],vis[N][N][5],dis[N][N][5];
int gi()
{
int x=0,res=1;char ch=getchar();
while(ch>\'9\'||ch<\'0\'){if(ch==\'-\')res*=-1;ch=getchar();}
while(ch<=\'9\'&&ch>=\'0\')x=x*10+ch-48,ch=getchar();
return x*res;
}
inline bool check(int x,int y)
{
if(x<1 || y<1 || x>n || y>m)return false;
return map[x][y];
}
inline int fc(int x)
{
if(x!=2)return (x+2)%4;
return 4;
}
inline int BFS(int fx,int fy,int tx,int ty)
{
int Vis[N][N],dep[N][N];
memset(Vis,0,sizeof(Vis));
memset(dep,127,sizeof(dep));
queue<Dot>Q;Q.push((Dot){fx,fy});
Vis[fx][fy]=1;dep[fx][fy]=0;
while(!Q.empty()){
Dot now=Q.front();Q.pop();
int x=now.x,y=now.y;Vis[x][y]=0;
for(int i=1;i<=4;++i)
if(check(x+Gx[i],y+Gy[i]))
if(dep[x][y]+1<dep[x+Gx[i]][y+Gy[i]]){
int xx=x+Gx[i],yy=y+Gy[i];
dep[xx][yy]=dep[x][y]+1;
if(!Vis[xx][yy]){
Vis[xx][yy]=1;
Q.push((Dot){xx,yy});
}
}
}
return dep[tx][ty]==dep[0][0]?far[0][0][0][0]:dep[tx][ty];
}
inline void prepare()
{
memset(far,127,sizeof(far));
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
if(map[i][j]){
map[i][j]=0;
for(int k=1;k<=4;++k)
if(check(i+Gx[k],j+Gy[k]))
for(int l=1;l<=4;++l)
if(check(i+Gx[l],j+Gy[l]))
if(k!=l)
far[i][j][k][l]=BFS(i+Gx[k],j+Gy[k],i+Gx[l],j+Gy[l]);
else far[i][j][k][l]=0;
map[i][j]=1;
}
}
inline void solve()
{
if(check(Ex,Ey) && check(Sx,Sy) && check(Tx,Ty));
else{printf("-1\\n");return;}
memset(vis,0,sizeof(vis));
memset(dis,127,sizeof(dis));
for(int i=1;i<=4;++i)
vis[Sx][Sy][i]=1,dis[Sx][Sy][i]=0;
queue<Data>Q;map[Sx][Sy]=0;
for(int i=1;i<=4;++i)
if(check(Sx+Gx[i],Sy+Gy[i])){
int d=BFS(Ex,Ey,Sx+Gx[i],Sy+Gy[i]);
if(d<far[0][0][0][0]){
dis[Sx+Gx[i]][Sy+Gy[i]][fc(i)]=d+1;
vis[Sx+Gx[i]][Sy+Gy[i]][fc(i)]=1;
Q.push((Data){Sx+Gx[i],Sy+Gy[i],fc(i)});
}
}
map[Sx][Sy]=1;
while(!Q.empty()){
Data now=Q.front();Q.pop();
int x=now.x,y=now.y,from=now.from;
vis[x][y][from]=0;
for(int i=1;i<=4;++i)
if(check(x+Gx[i],y+Gy[i])){
int xx=x+Gx[i],yy=y+Gy[i];
int dt=far[x][y][from][i];
if(dis[x][y][from]+dt+1<dis[xx][yy][fc(i)]){
dis[xx][yy][fc(i)]=dis[x][y][from]+dt+1;
if(!vis[xx][yy][fc(i)]){
Q.push((Data){xx,yy,fc(i)});
vis[xx][yy][fc(i)]=1;
}
}
}
}
int ans=dis[0][0][0];
for(int i=1;i<=4;++i)ans=min(ans,dis[Tx][Ty][i]);
if(ans==dis[0][0][0])printf("-1\\n");
else printf("%d\\n",ans);
}
int main()
{
n=gi();m=gi();Q=gi();
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
map[i][j]=gi();
prepare();
while(Q--){
Ex=gi();Ey=gi();
Sx=gi();Sy=gi();
Tx=gi();Ty=gi();
if(Sx==Tx && Sy==Ty){
printf("0\\n");
continue;
}
solve();
}
return 0;
}
5.NOIP2015斗地主
给你几张牌,给你一些规则,问你这些牌最少几步打完。牌数不超过23张。
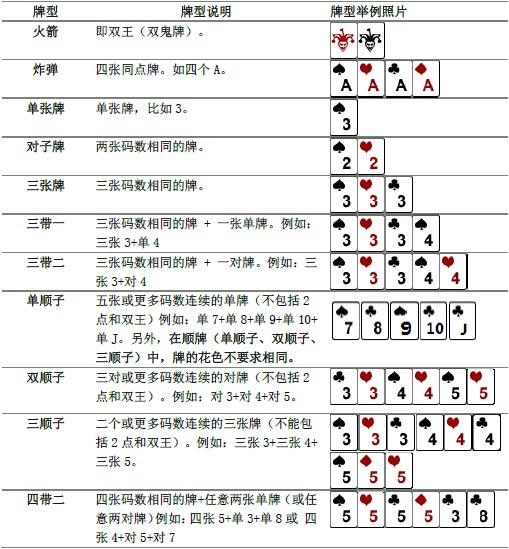
一个剪枝:先把四带、三带等打完,粗略计算答案上界。
我也不知道为什么要先带掉单个的。
然后就是很简单的爆搜2333了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <complex>
#include <stack>
#define LL long long int
#define ls (x << 1)
#define rs (x << 1 | 1)
#define MID int mid=(l+r)>>1
using namespace std;
int bin[21],Ans,n,T;
int gi()
{
int x=0,res=1;char ch=getchar();
while(ch>\'9\'||ch<\'0\'){if(ch==\'-\')res*=-1;ch=getchar();}
while(ch<=\'9\'&&ch>=\'0\')x=x*10+ch-48,ch=getchar();
return x*res;
}
inline bool check_UP()
{
for(int i=1;i<=14;++i)
if(bin[i])return false;
return true;
}
inline void dfs(int step)
{
if(step>=Ans)return;
if(check_UP()){Ans=step;return;}
int s1,s2,s3,s4;s1=s2=s3=s4=0;
for(int i=1;i<=14;++i){
if(bin[i]==1)++s1;
if(bin[i]==2)++s2;
}
for(int i=1;i<=13;++i)
if(bin[i]==4){
s4++;
if(s1>=2)s1-=2;
else if(s2>=2)s2-=2;
else s1--;
}
for(int i=1;i<=13;++i)
if(bin[i]==3){
s3++;
if(s1)s1--;
else if(s2)s2--;
}
Ans=min(Ans,step+s1+s2+s3+s4);
//三顺子!
for(int i=1;i<=11;++i)
if(bin[i]>=3 && bin[i+1]>=3){
int j=i+2;
bin[i]-=3;bin[i+1]-=3;
dfs(step+1);
while(bin[j]>=3 && j<=12)bin[j]-=3,dfs(step+1),++j;
for(int k=i;k<j;++k)bin[k]+=3;
}
//Congratulations!
//双顺子!
for(int i=1;i<=10;++i)
if(bin[i]>=2 && bin[i+1]>=2 && bin[i+2]>=2){
int j=i+3;
bin[i]-=2;bin[i+1]-=2;bin[i+2]-=2;
dfs(step+1);
while(bin[j]>=2 && j<=12)bin[j]-=2,dfs(step+1),++j;
for(int k=i;k<j;++k)bin[k]+=2;
}
//Congratulations!
//单顺子!
for(int i=1;i<=8;++i)
if(bin[i]>=1 && bin[i+1]>=1 && bin[i+2]>=1 && bin[i+3]>=1 && bin[i+4]>=1){
int j=i+5;
bin[i]--;bin[i+1]--;bin[i+2]--;bin[i+3]--;bin[i+4]--;
dfs(step+1);
while(bin[j]>=1 && j<=12)bin[j]--,dfs(step+1),++j;
for(int k=i;k<j;++k)bin[k]++;
}
//Congratulations!
/*
//四带一/二!
for(int i=1;i<=13;++i)
if(bin[i]==4){
bin[i]-=4;
for(int j=1;j<=14;++j)
if(bin[j]>=2)
for(int k=1;k<=14;++k)
if(bin[k]>=2){
bin[j]-=2;bin[k]-=2;
dfs(step+1);
bin[j]+=2;bin[k]+=2;
}
for(int j=1;j<=14;++j)
if(bin[j]>=1)
for(int k=1;k<=14;++k)
if(bin[k]>=1){
bin[j]-=1;bin[k]-=1;
dfs(step+1);
bin[j]+=1;bin[k]+=1;
}
bin[i]+=4;
}
//Congratulations!
//三带二!
for(int i=1;i<=13;++i)
if(bin[i]>=3){
bin[i]-=3;
for(int j=1;j<=14;++j)
if(bin[j]>=2){
bin[j]-=2;
dfs(step+1);
bin[j]+=2;
}
bin[i]+=3;
}
//Congratulations!
//三带一!(附炸弹)
for(int i=1;i<=13;++i)
if(bin[i]>=3){
bin[i]-=3;
for(int j=1;j<=14;++j)
if(bin[j]>=1){
bin[j]-=1;
dfs(step+1);
bin[j]+=1;
}
bin[i]+=3;
}
//Congratulations!
//三张牌!
for(int i=1;i<=13;++i)
if(bin[i]>=3){bin[i]-=3;dfs(step+1);bin[i]+=3;}
//Congratulations!
//对子牌!
for(int i=1;i<=14;++i)
if(bin[i]>=2){bin[i]-=2;dfs(step+1);bin[i]+=2;}
//Congratulations!
//单张!
for(int i=1;i<=14;++i)
if(bin[i]==1){bin[i]-=1;dfs(step+1);bin[i]+=1;}
//Congratulations!
*/
}
int main()
{
scanf("%d%d",&T,&n);
while(T--){
memset(bin,0,sizeof(bin));Ans=n;
for(int i=1;i<=n;++i){
int x=gi();gi();
if(x==0)bin[14]++;
else if(x==1 || x==2)bin[x+11]++;
else bin[x-2]++;
}
dfs(0);
printf("%d\\n",Ans);
}
return 0;
}
以上是关于历年NOIP中的搜索题的主要内容,如果未能解决你的问题,请参考以下文章