算法排序学习

Posted 2020-09-27 胡图咦声

1：冒泡排序

已知一组无序数据a[1]、a[2]、……a[n]，需将其按升序排列。首先比较a[1]与a[2]的值，若a[1]大于a[2]则交换两者的值，否则不变。再比较a[2]与a[3]的值，若a[2]大于a[3]则交换两者的值，否则不变。再比较a[3]与a[4]，以此类推，最后比较a[n-1]与a[n]的值。这样处理一轮后，a[n]的值一定是这组数据中最大的。再对a[1]~a[n-1]以相同方法处理一轮，则a[n-1]的值一定是a[1]~a[n-1]中最大的。再对a[1]~a[n-2]以相同方法处理一轮，以此类推。共处理n-1轮后a[1]、a[2]、……a[n]就以升序排列了。降序排列与升序排列相类似，若a[1]小于a[2]则交换两者的值，否则不变，后面以此类推。 总的来讲，每一轮排序后最大（或最小）的数将移动到数据序列的最后，理论上总共要进行n(n-1）/2次交换。

public static void BubbleSort(this int[] arry)
 6         {
 7             for (int i = 0; i < arry.Length-1; i++)
 8             {
 9                 for (int j = 0; j < arry.Length - 1 - i; j++)
10                 {
11                     //比较相邻的两个元素，如果前面的比后面的大，则交换位置
12                     if (arry[j] > arry[j + 1])
13                     {
14                         int temp = arry[j + 1];
15                         arry[j + 1] = arry[j];
16                         arry[j] = temp;
17                     }
18                 }
19             }
20         }

优点：稳定

缺点：慢，每次只移动相邻的两个元素。

时间复杂度：理想情况下（数组本来就是有序的），此时最好的时间复杂度为o(n),最坏的时间复杂度(数据反序的)，此时的时间复杂度为o(n*n) 。冒泡排序的平均时间负责度为o(n*n).

2:快速排序

设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。
一趟快速排序的算法是：
1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；
2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；
3）从j开始向前搜索，即由后开始向前搜索(j--)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；
4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；
5）重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）。

  public static void QuickSort(this int[] arry, int left, int right)
 8         {
 9             //左边索引小于右边，则还未排序完成 　　
10             if (left < right)
11             {
12                 //取中间的元素作为比较基准，小于他的往左边移，大于他的往右边移 　　
13                 int middle = arry[(left + right) / 2];
14                 int i = left - 1;
15                 int j = right + 1;
16                 while (true)
17                 {
18                     //移动下标，左边的往右移动，右边的向左移动
19                     while (arry[++i] < middle && i < right);
20                     while (arry[--j] > middle && j > 0);
21                     if (i >= j)
22                         break;
23                     //交换位置
24                     int number = arry[i];
25                     arry[i] = arry[j];
26                     arry[j] = number;
27 
28                 }
29                 QuickSort(arry, left, i - 1);
30                 QuickSort(arry, j + 1, right);
31             }
32         }

 

具体快速排序的规则一般如下：

从右边开始查找比66小的数，找到的时候先等一下，再从左边开始找比66大的数，将这两个数借助66互换一下位置，继续这个过程直到两次查找过程碰头。

例子中：

66  13  51  76  81  26  57  69  23

从右边找到23比66小，互换

23  13  51  76  81  26  57  69  66

从左边找到76比66大，互换

23  13  51  66  81  26  57  69  76

继续从右边找到57比66小，互换

23  13  51  57  81  26  66  69  76

从左边查找，81比66大，互换

23  13  51  57  66  26  81  69  76

从右边开始查找26比66小，互换

23  13  51  57  26  66  81  69  76

从左边开始查找，发现已经跟右边查找碰头了，结束，第一堂排序结束

快速排序算法的时间复杂度，有时候是O(nlgn), 有时候就是O(n2), 在你不知道自己数据特性的情况下，很难选择是否使用快速排序，因为他并不总是最快的。

 

 

 

主定理: T [n] = aT[n/b] + f (n)

其中 a >= 1 and b > 1 是常量 并且 f (n) 是一个渐近正函数， 为了使用这个主定理，您需要考虑下列三种情况：

 

 

 

 

快速排序的每一次划分把一个 问题分解成两个子问题，其中的关系可以用下式表示：

 

T[n] = 2T[n/2] + O(n) 其中O(n)为PARTITION()的时间复杂度，对比主定理，

 

 T [n] = aT[n/b] + f (n)

 

我们的快速排序中：a = 2, b = 2, f(n) = O(n)

 

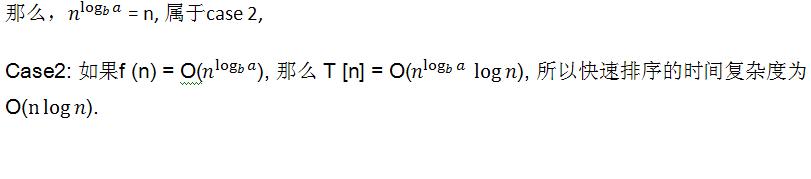
那么为什么还有最坏情况呢？

 

考虑如下极端情况，

 

T[n] = T[n-1] + T[1] + O(n),

问题来了，这一次的划分白玩了，划分之后一边是一个，一边是n-1个，这种极端情况的时间复杂度就是O(n2).

而对于其他常数比例划分，哪怕是左右按9:1的比例划分，效果都是和在正中间划分一样快的（算法导论上有详细分析）

即，任何一种按照常数比例进行划分，总运行时间都是O（n lg n）