#define lowbit(x) ((x)&(-x))原理详解

Posted 2020-06-25 志银

#define lowbit(x) ((x)&(-x)) 

也可以写成如下形式：

int Lowbit(x) {

  return x&(-x);

}

例如：

1> x = 1:

十进制转二进制（设位数为８）：

1 => 0000 0001

-1=> 1111 1111(此处为1的补码)

1&(-1)的二进制位运算为(同1异0)：

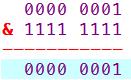
所以1&(-1)=1

2> x = 6:

十进制转二进制（设位数为８）：

6 => 0000 0110

-6=> 1111 1010(此处为6的补码)

6&(-6)的二进制位运算为(同1异0)：

所以6&(-6)=2

总结：

求出2^p(其中p: x 的二进制表示数中， 右向左数第一个1的位置)，

如6的二进制表示为110，向左数第零个为0，第一个为1，则p=1，

故Lowbit(6) = 2^1 = 2。

或直接理解为：二进制按位与运算，返回不大于x的2的最大次方因子

                                                                                                        开始于：2016-03-18、16:37:32