Bellman-Ford算法
Posted siwuxie095
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Bellman-Ford算法相关的知识,希望对你有一定的参考价值。
------------------siwuxie095
Bellman-Ford 算法
这里介绍 Bellman-Ford 算法,和 Dijkstra 算法一样,
它也是一个单源最短路径算法
Bellman-Ford 算法解决了 Dijkstra 算法没有解决的问
题:负权边问题,即 Bellman-Ford 算法中可以引入负
权边
看如下实例:
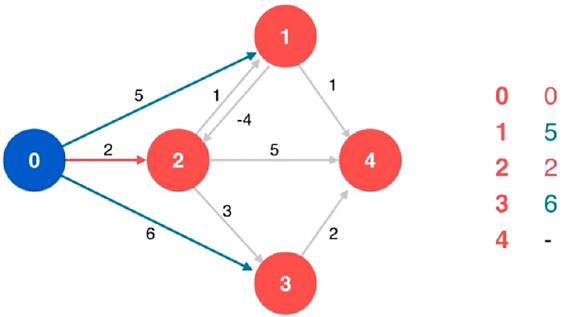
顶点 1 到顶点 2 的负权边的存在,使得虽然当前从顶点 0 到
顶点 1 的权值远远的高于从顶点 0 到顶点 2 的权值,但在绕
道的过程中,负权边让大部分权值都抵消了,反而低于从顶点
0 到顶点 2 的权值
即 0 -> 1 -> 2 的路径比 0 -> 2 的路径更短,如下:
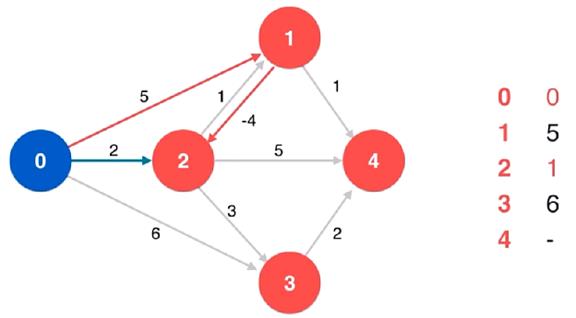
不难看出,表面是在处理负权边,但本质上仍然是一次
松弛操作
换言之,虽然负权边使得 Dijkstra 算法失效了,但依然
要依赖松弛操作
Bellman-Ford 算法虽然解决了负权边问题,但它也有
一定的局限性
看如下实例:
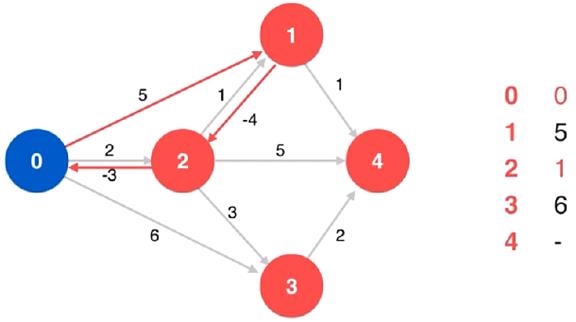
多出一条从顶点 2 到顶点 0 的负权边,就形成了一个负权环,
0 -> 1 -> 2 -> 0 这条路径的总权值为 -2
当一个图中出现了负权环,那么从一点到任何一点只要能经
过该负权环,权值就会更小,而想要找到所谓的最短路径,
就一定要不停地在该负权环中转。因为每转一圈,得到的总
权值就更小
这样一来,相当于图中就不存在最短路径了,或 最短路径的
结果是负无穷
所以,在处理带有负权边的图时,如果图中拥有负权环,则
该图就不再拥有最短路径
「拥有负权环的图,没有最短路径」
注意:不要认为负权环一定至少由三个顶点组成,事实上,
两个顶点之间也可以形成负权环,如下图所示

综上,Bellman-Ford 算法解决的就是图中可以有负权边,
但不能有负权环的单源最短路径问题
「前提:图中不能有负权环」
不过 Bellman-Ford 算法比想象中更加出色,它不一定要
遵守该前提。如果图中有负权环,Bellman-Ford 算法经
过运行之后,虽然找不到最短路径,但是可以判断出图中
有负权环
「Bellman-Ford 算法可以判断图中是否有负权环」
Bellman-Ford 算法如此神奇,相应的代价也是高昂的,
它的时间复杂度:O(E*V)
Bellman-Ford 算法的基本思想:
如果一个图中没有负权环,从一点到另外一点的最短路径,
最多经过所有 V 个顶点,有 V-1 条边,否则,存在顶点被
经过了两次,即 存在负权环
看如下实例:
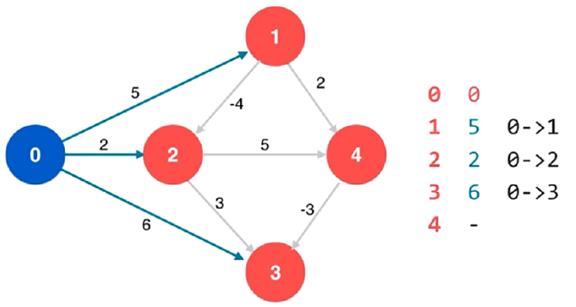
左边是一张连通带权有向图,右边是起始顶点 0 到各个顶点的
当前最短距离的列表,起始顶点 0 到自身的距离是 0
将顶点 0 进行标识,并作为当前顶点。对当前顶点 0 的所有相
邻顶点依次进行一次松弛操作,同时更新列表
然后将当前顶点 0 的所有相邻顶点依次当做新的当前顶点,并
对新的当前顶点的所有相邻顶点依次进行一次松弛操作,同时
更新列表
… …
对当前顶点进行一次松弛操作,就是找到了经过当前顶点的另
外一条路径,多一条边,权值更小
如果一个图中没有负权环,从一点到另外一点的最短路径,最
多经过所有 V 个顶点,有 V-1 条边
对所有顶点进行 V-1 次松弛操作,理论上就找到了从起始顶点
到其它所有顶点的最短路径
然后再尝试对所有顶点进行第 V 次松弛操作, 如果还可以继续
松弛,就说明图中一定存在负权环
注意:Bellman-Ford 算法主要针对有向图,因为如果是无向图,
一旦图中存在负权边,就相当于存在负权环,而如果图中没有负
权边,就可以直接使用 Dijkstra 算法,效率更高
程序:
Edge.h:
|
#ifndef EDGE_H #define EDGE_H
#include <iostream> #include <cassert> using namespace std;
//边信息:两个顶点和权值 template<typename Weight> class Edge {
private:
int a, b; //边的两个顶点a和b(如果是有向图,就默认从顶点a指向顶点b) Weight weight; //边上的权值
public:
Edge(int a, int b, Weight weight) { this->a = a; this->b = b; this->weight = weight; }
//默认构造函数 Edge(){}
~Edge(){}
int v(){ return a; }
int w(){ return b; }
Weight wt() { return weight; }
//知道边的一个顶点x,返回另一个顶点 int other(int x) { assert(x == a || x == b); return x == a ? b : a; }
//友元函数重载 friend ostream &operator<<(ostream &os, const Edge &e) { os << e.a << "-" << e.b << ": " << e.weight; return os; }
bool operator<(Edge<Weight> &e) { return weight < e.wt(); }
bool operator<=(Edge<Weight> &e) { return weight <= e.wt(); }
bool operator>(Edge<Weight> &e) { return weight > e.wt(); }
bool operator>=(Edge<Weight> &e) { return weight >= e.wt(); }
bool operator==(Edge<Weight> &e) { return weight == e.wt(); } };
#endif |
SparseGraph.h:
|
#ifndef SPARSEGRAPH_H #define SPARSEGRAPH_H
#include "Edge.h" #include <iostream> #include <vector> #include <cassert> using namespace std;
// 稀疏图 - 邻接表 template<typename Weight> class SparseGraph {
private:
int n, m; //n 和 m 分别表示顶点数和边数 bool directed; //directed表示是有向图还是无向图 vector<vector<Edge<Weight> *>> g; //g[i]里存储的就是和顶点i相邻的所有边指针
public:
SparseGraph(int n, bool directed) { this->n = n; this->m = 0; this->directed = directed; //g[i]初始化为空的vector for (int i = 0; i < n; i++) { g.push_back(vector<Edge<Weight> *>()); } }
~SparseGraph() {
for (int i = 0; i < n; i++) { for (int j = 0; j < g[i].size(); j++) { delete g[i][j]; } } }
int V(){ return n; } int E(){ return m; }
void addEdge(int v, int w, Weight weight) { assert(v >= 0 && v < n); assert(w >= 0 && w < n);
g[v].push_back(new Edge<Weight>(v, w, weight)); //(1)顶点v不等于顶点w,即不是自环边 //(2)且不是有向图,即是无向图 if (v != w && !directed) { g[w].push_back(new Edge<Weight>(w, v, weight)); }
m++; }
//hasEdge()判断顶点v和顶点w之间是否有边 //hasEdge()的时间复杂度:O(n) bool hasEdge(int v, int w) { assert(v >= 0 && v < n); assert(w >= 0 && w < n);
for (int i = 0; i < g[v].size(); i++) { if (g[v][i]->other(v) == w) { return true; } }
return false; }
void show() {
for (int i = 0; i < n; i++) { cout << "vertex " << i << ":\\t"; for (int j = 0; j < g[i].size(); j++) { cout << "{to:" << g[i][j]->w() << ",wt:" << g[i][j]->wt() << "}\\t"; } cout << endl; } }
//邻边迭代器(相邻,即 adjacent) // //使用迭代器可以隐藏迭代的过程,按照一定的 //顺序访问一个容器中的所有元素 class adjIterator { private:
SparseGraph &G; //图的引用,即要迭代的图 int v; //顶点v int index; //相邻顶点的索引
public:
adjIterator(SparseGraph &graph, int v) : G(graph) { this->v = v; this->index = 0; }
//要迭代的第一个元素 Edge<Weight> *begin() { //因为有可能多次调用begin(), //所以显式的将index设置为 |