[算法]：分治法-求大整数相乘

Posted 2020-09-27 懒惰的咕噜

#问题
大整数相乘

#思路说明

对于大整数计算，一般都要用某种方法转化，否则会溢出。但是python无此担忧了。

Python支持**“无限精度”的整数，**一般情况下不用考虑整数溢出的问题，而且Python Int类型与任意精度的Long整数类可以无缝转换，超过Int 范围的情况都将转换成Long类型。

例如：

    >>> 2899887676637907866*1788778992788348277389943

    5187258157415700236034169791337062588991638L

注意：前面的“无限精度”是有引号的。事实上也是有限制的，对于32位的机器，其上限是：2^32-1。真的足够大了。

为什么Python能够做到呢？请有兴趣刨根问底的去看Python的有关源码。本文不赘述。

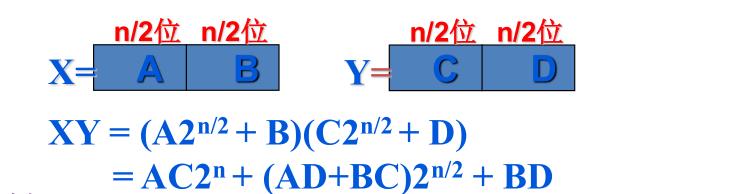
在其它语言中，通常用“分治法”解决大整数相乘问题。


再次化简 ：XY=AC2^n+[(A-B)(D-C)+AC+BD]2^n/2+BD
此算法要求X，Y必须位数相同，并且位数是2的n次方
所以：1.用数组保存，不满足条件则在前面补0
　　　2.相乘时给短的补0，直至X,Y位数相同
　　  3.递归

import math
import copy


class big_int(list):
    def __init__(self, num):
        self.neg = 1
        for i in str(num):
            if i == \'-\':
                self.neg = -1
                continue
            self.append(int(i))
        m =math.log(len(self), 2)
        if m!=int(m):
            m=int(m)+1
            while len(self) != pow(2, m):
                self.insert(0, 0)


    @classmethod
    def minusa(cls,l1,l2):
        l1 = int(str(l1).replace(\'[\',\'\').replace(\']\',\'\').replace(\',\',\'\').replace(\' \',\'\'))
        l2 = int(str(l2).replace(\'[\', \'\').replace(\']\', \'\').replace(\',\', \'\').replace(\' \',\'\'))
        return l1-l2


    def __aspect(self,L1,L2):
        l1=copy.copy(L1)
        l2=copy.copy(L2)
        N = len(l1)/2
        if N==0:
            return l1.neg*l2.neg*(l1[0]*l2[0])
        A = l1[:N]
        B = l1[N:]
        C = l2[:N]
        D = l2[N:]
        if N == 1:
            return l1.neg*l2.neg*(A[0]*C[0]*100 +((A[0]-B[0])*(D[0]-C[0])+A[0]*C[0]+B[0]*D[0])*10+B[0]*D[0])
        else:
            A_,B_,C_,D_=\'\',\'\',\'\',\'\'
            for i in A:
                A_ += str(i)
            for i in B:
                B_ += str(i)
            for i in C:
                C_ += str(i)
            for i in D:
                D_ += str(i)
            A = big_int(A_)
            B = big_int(B_)
            C = big_int(C_)
            D = big_int(D_)
            AC = A.__mul__(C)
            BD = B.__mul__(D)
            A_B = big_int(big_int.minusa(A,B))
            D_C = big_int(big_int.minusa(D,C))
        return l1.neg*l2.neg*(AC*pow(10,2*N)+(A_B.__mul__(D_C)+AC+BD)*pow(10,N)+BD)


    def __fillzero_mul(self, other):
        if len(self)>len(other):
            while(len(other)<len(self)):
                other.insert(0,0)
        else:
            while (len(self)<len(other)):
                self.insert(0,0)
        return self.__aspect(self,other)


    def __mul__(self, other):
        if type(other) is not big_int:
            raise
        return self.__fillzero_mul(other)

参考资料：http://blog.csdn.net/jeffleo/article/details/53446095
https://github.com/qiwsir/algorithm