进制转换与数字存储实例

Posted 2020-09-27

　　说明：本实例基于C语言编写

一、进制转换

　　1）、十进制转其它进制

• 　　DEC转BIN：N=25

　　(25)₂=11001

　　

 

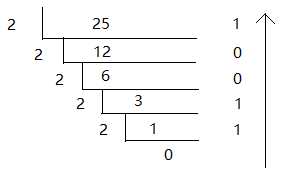
• 　　DEC转OCT：N=125

　　(125)₈=175

　　

 

• 　　DEC转HEX：N=2581

　　(2581)₁₆=A15

　　

 

　　2）、其它进制转十进制

• 　　BIN转DEC：(1100101)₂

　　(1100101)₂=1x2⁶+1x2⁵+0x2⁴+0x2³+1x2²+0x2¹+1x2⁰=64+32+0+0+4+0+1=101

• 　　OCT转DEC：(2612)₈

　　(2612)₈=2x8³+6x8²+1x8¹+2x8⁰=1024+384+8+2=1418

• 　　HEX转DEC：(A46C)₁₆

　　(A46C)₁₆=10x16³+4x16²+6x16¹+12x16⁰=40960+1024+96+12=42092

　　3）、二进制与八进制互转

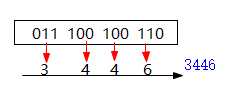
• 　　BIN转OCT：(011100100110)₂

　　(011100100110)₂=(3446)₈

　　

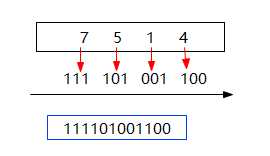
• 　　OCT转BIN：(7514)₈

　　(7514)₈=(?111101001100?)₂

　　

　　4）、二进制与十六进制互转

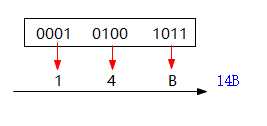
• 　　BIN转HEX：(0101001011)₂

　　(0101001011)₂=(14B)₁₆

　　

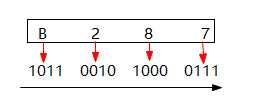
• 　　HEX转BIN：(B287)₁₆

　　(B287)₁₆=(?1011001010000111?)₂

　　

　　5）、八进制与十六进制互转

　　OCT转HEX：OCT转BIN转HEX

　　HEX转OCT：HEX转BIN转OCT

二、数字存储

　　1）、无符号整数原码存储：N=126

　　

　　

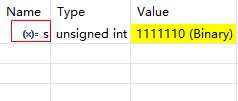
　　2）、有符号正整数原码存储：N=126

　　参照上一个例子

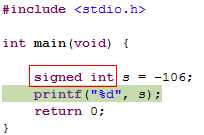
　　3）、有符号负整数补码存储：-106

　　(106)₂=00000000000000000000000001101010

　　如果用4字节（32位来存储）的话，(106)_补=11111111111111111111111110010110

　　

　　

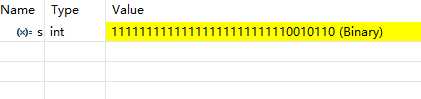
　　将补码存储的有符号负整数还原为十进制数

• 　　对补码表示的数进行补码运算得到这个十进制数的绝对值的二进制表示：01101010
•        将该二进制数转换为十进制并添加符号(看最高位)即可：-10

　　补码运算

　　

　　4）、单精度浮点数存储：余127码

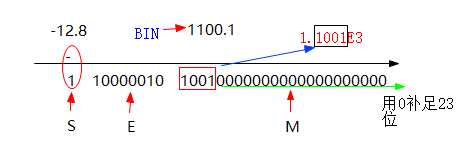
　　N = - 12.8（精度2位）

• 　　符号位S=1（负数）
• 　　转化为二进制表示：(12.8)₂=(1100.1)₂，转换为二进制的小数部分精度为1
• 　　规范化：(1.1001)x2³
• 　　指数E=3+127=130，二进制为：(130)₂=(10000010)₂
• 　　尾数M=(10010000000000000000000)₂
• 　　结果：1 10000010 10010000000000000000000

　　

　　5）、双精度浮点数存储：余1023码

　　操作方法和单精度浮点数的存储一直，不同的是，双精度浮点数的指数E用11位存储，尾数用52位存储。