树状数组

Posted 2020-09-26 YXY_1211

    首先，我们需要了解一下数在计算机中的储存方式。

以68为例，他的二进制是（68）₂=1000100. 那么-68呢？因为计算机里的整数采用补码表示（补码是原码取反加一），因此-68实际上是68按位取反，末尾加一以后的结果。如下表（忽略符号位）：

原码   1 0 0 0 1 0 0

          ↓

反码   0 1 1 1 0 1 1

         ↓

补码   0 1 1 1 1 0 0

我们把（68）₂和（-68）₂放在一起看一看：

1 0 0 0 1 0 0

0 1 1 1 1 0 0

发现他们末尾带的0是一样多的。因此lowbit(x)=x&-x.   （&是转换成二进制之后进行与运算；而&&是直接进行与运算）

---

下面是一个比较经典的树状数组（BIT）：

 

↓     ↓     ↓     ↓    ↓     

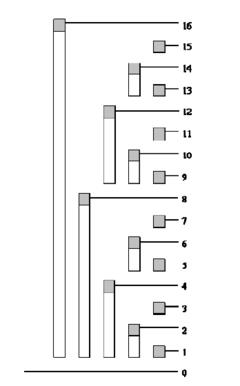
 lowbit   =   2⁴   2³     2²   2¹   2⁰                                  

从图中可以得到以下规律：

1）对于结点i，如果他是左子结点（下左上右），那么他父节点的编号就是i+lowbit(i)；如果他是右子节点，那么他父节点的编号就是i-lowbit(i)。（i>=lowbit(i)）

2）奇数的lowbit之所以都是1，是因为他们的二进制个位就是1（即因数没有2）。后面的以此类推：2、6、10、14只能整除2¹，4、12可以整除2²……因此他们的lowbit依次是2、3……

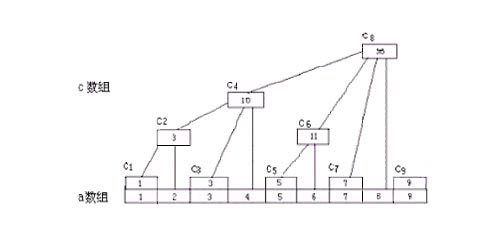
在以上规律的基础上，我们新建一个数组C（A是原数组），则易得：

C_i=A_{i-lowbit(i)+1}+A_{i-lowbit(i)+2}+……+A_i

举例：C1=A1,C2=A1+A2,C3=A3,C4=A1+A2+A3+A4,……

---

 接下来是一些应用：

1）求前缀和S_i：顺着结点i向上，依次找到i左上侧的每个结点j，每个结点的C_j加起来即为结点i的前缀和（如下图）。

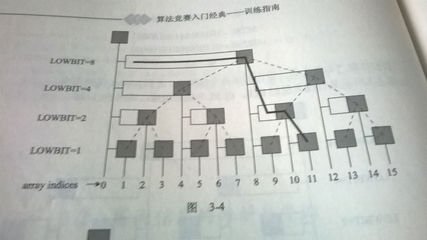
2）更新数据：如果修改了一个A_i，如何计算前缀和S_i？顺着结点i向上，依次找到i右上侧的每个结点j，修改每个结点的C_j 即可。