割点与桥

Posted 2020-09-26 lh

割点与桥

题目描述

给定一张无向图G(V,E),你需要找出所有的割点与桥.

输入

第一行给出两个正整数V,E.

接下来E行每行两个正整数x,y，表示有一条连接x,y的边。

输出

输出共2行，第一行输出所有割点的编号，第二行输出所有桥的编号。

样例输入

7 8
1 2
1 3
1 7
2 3
3 4
3 5
4 5
5 6

样例输出

1 3 5 
3 8 

提示

 

割点与桥的定义：

割点：若删掉某点后，原连通图分裂为多个子图，则称该点为割点。

割边(桥)：删掉它之后，图必然会分裂为两个或两个以上的子图。

割点与桥分别按从小到大的顺序输出

1<=V,E<=5*10^5

保证无重边与自环

 

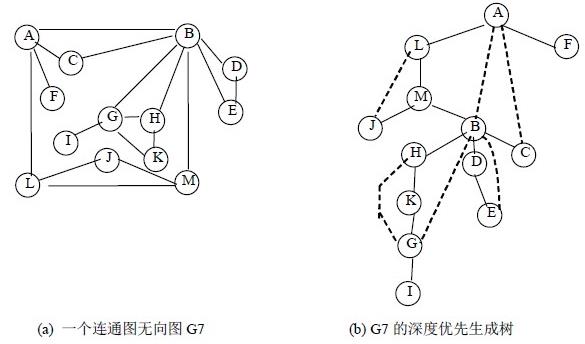
 DFS搜索树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树，如图(b)所示。

树边：在搜索树中的实线所示，可理解为在DFS过程中访问未访问节点时所经过的边。

回边：在搜索树中的虚线所示，可理解为在DFS过程中遇到已访问节点时所经过的边。

求割点：

该算法是R.Tarjan发明的。观察DFS搜索树，我们可以发现有两类节点可以成为割点：

1.对根节点u，若其有两棵或两棵以上的子树，则该根结点u为割点；

2.对非叶子节点u（非根节点），若其子树的节点均没有指向u的祖先节点的回边，说明删除u之后，根结点与u的子树的节点不再连通；则节点u为割点。

对于根结点，显然很好处理；但是对于非叶子节点，怎么去判断有没有回边是一个值得深思的问题。

我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点（即DFS次序号最小），那么low[u]的计算过程如下：

下表给出图(a)对应的dfn与low数组值。

i	0	1	2	3	4	5	6	7	8	9	10	11	12
vertex	A	B	C	D	E	F	G	H	I	J	K	L	M
dfn[i]	1	5	12	10	11	13	8	6	9	4	7	2	3
low[i]	1	1	1	5	5	1	5	5	8	2	5	1	1

对于情况2，当(u,v)为树边且low[v] >= dfn[u]时，节点u才为割点。该式子的含义：以节点v为根的子树所能追溯到最早的祖先节点要么为v要么为u。

求桥：

在割点操作的基础上，求桥只要一个判断，当low[v]==dfn[v]且（u，v）为树边时，边（u，v）才是桥。

注意：这张图有可能不连通，桥的编号只要按输入顺序建链表，找到一座桥后，把它在链表里的位置/2即可（因为边是双向的），链表下标要从2开始

#include<iostream> 
#include<cstdio> 
using namespace std; 
int n,m,dfn[500002],low[500002],t=0,tot=0;bool point[500002],a[500002],bridge[500002]; 
int ch=0,to[1000004],nxt[1000004],h[500002],k=1;
inline int read(){  
    register int x;register bool f;register char c;  
    for (f=0; (c=getchar())<\'0\'||c>\'9\'; f=c==\'-\');  
    for (x=c-\'0\'; (c=getchar())>=\'0\'&&c<=\'9\'; x=(x<<3)+(x<<1)+c-\'0\');  
    return f?-x:x;  
}  
inline void ins(int x,int y){to[++k]=y,nxt[k]=h[x],h[x]=k;}  
void dfs(int x,int fa) 
{ 
    dfn[x]=++t;low[x]=dfn[x];a[x]=1; 
    for(int i=h[x];i;i=nxt[i]) 
    { 
        int y=to[i];if(y==fa)continue; 
        if(!dfn[y]) 
        { 
            dfs(y,x);low[x]=min(low[x],low[y]); 
            if(low[y]>=dfn[x])point[x]=1;if(x==fa)ch++; 
            if(low[y]==dfn[y])bridge[i>>1]=1; 
        } 
        else low[x]=min(low[x],dfn[y]); 
    } 
} 
int main() 
{ 
    int n=read(),m=read(); 
    for(int i=1;i<=m;i++) 
    { 
        int u,v;u=read();v=read();
        ins(v,u);ins(u,v); 
    } 
    for(int i=1;i<=n;i++) 
    { 
        if(!a[i]) 
        { 
            ch=0;dfs(i,i);if(ch<=1)point[i]=0; 
        } 
    } 
    for(int i=1;i<=n;i++)if(point[i])printf("%d ",i);puts(""); 
    for(int i=1;i<=m;i++)if(bridge[i])printf("%d ",i); 
    return 0; 
} 

 学校网络(poj_1236)

Sample Input

5
2 4 3 0
4 5 0
0
0
1 0

Sample Output

1
2

定义：
强连通图：在一个强连通图中，任意两个点都通过一定路径互相连通。
强连通分量。在一个非强连通图中极大的强连通子图就是该图的强连通分量。
求强连通分量：在割点操作的基础上，加上这几个操作且low可以通过父子边(树边)转移

1. 堆栈：每搜索到一个点，将它压入栈顶。
2. 对于回边，要保证v点在栈中，才能更新。（即横叉边不更新）
3. 每当搜索到一个点经过以上操作后（也就是子树已经全部遍历）的low值等于dfn值，则将它以及在它之上的元素弹出栈。这些出栈的元素组成一个强连通分量。
4. 继续搜索（或许会更换搜索的起点，因为整个有向图可能分为两个不连通的部分），直到所有点被遍历。

Tarjan算法的操作原理如下：

1. Tarjan算法基于定理：在任何深度优先搜索中，同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。也就是说，强连通分量一定是有向图的某个深搜树子树。
2. 可以证明，当一个点既是强连通子图Ⅰ中的点，又是强连通子图Ⅱ中的点，则它是强连通子图Ⅰ∪Ⅱ中的点。
3. 这样，我们用low值记录该点所在强连通子图对应的搜索子树的根节点的Dfn值。注意，该子树中的元素在栈中一定是相邻的，且根节点在栈中一定位于所有子树元素的最下方。
4. 强连通分量是由若干个环组成的。所以，当有环形成时（也就是搜索的下一个点已在栈中），我们将这一条路径的low值统一，即这条路径上的点属于同一个强连通分量。
5. 如果遍历完整个搜索树后某个点的dfn值等于low值，则它是该搜索子树的根。这时，它以上（包括它自己）一直到栈顶的所有元素组成一个强连通分量。

时间复杂度O（n+m）

分析此题的两个任务，很显然，因为一个强连通分量中的学校都可以互相传递文件，所以先缩点，把图变成一个DAG（有向无环图），

第一个任务：就是求新图中的入度为0的点的个数，因为这些点都不能通过其他学校来获得文件

第二个任务：max（入度为0，出度为0 ），通过缩点后，新图不一定连通，只要把出度为0的边连向入度为0的边即可。如图（红色的线表示连边）

 

 但是有一个特例，如果原图本身就强连通，那么第二问答案应为0，可缩点后新图只有一个点，按程序计算出来答案为1，所以应特判

（其实本题根本不需要建新图，具体见程序）

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
int low[101],dfn[101],ans[101],t=0,qlt[101],tot=0,nxt[20001],to[20001],h[101];
bool inq[101],in[101],out[101],a[101];int st[101],ht=0,k=0;
void ins(int x,int y){nxt[++k]=h[x];to[k]=y;h[x]=k;}
void tarjan(int x,int fa)
{a[x]=1;
    low[x]=dfn[x]=++t;inq[x]=1;st[++ht]=x;
    for(int i=h[x];i;i=nxt[i])
    {
        int y=to[i];
if(!dfn[y])
        {
            tarjan(y,x);
            low[x]=min(low[y],low[x]);
        }
        else if(inq[y])low[x]=min(low[x],dfn[y]);
    }
    if(low[x]==dfn[x])
    {
        ++tot;
        while(1)
        {
            int u=st[ht--];inq[u]=0;
            qlt[u]=tot;
            if(u==x)break;
        }
    }
}
int main()
{
    int n;scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int v;
        scanf("%d",&v);
        while(v)
        {
            ins(i,v);
            scanf("%d",&v); 
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(!a[i])tarjan(i,i);
    }
    for(int i=1;i<=n;i++) 
    {
        for(int j=h[i];j;j=nxt[j])
        {
            int v=to[j];if(qlt[i]==qlt[v])continue;
            out[qlt[i]]=1;in[qlt[v]]=1;
        }
    }
    if(tot==1)printf("1\\n0");
    else
    {
        int _in=0,_out=0;
        for(int i=1;i<=tot;i++)
        {
            if(!in[i])_in++;if(!out[i])_out++;
        }
        printf("%d\\n%d",_in,max(_in,_out));
    }
    return 0;
}

 点双连通分量：找割点，栈里存边

void tarjan(int x,int f)
{
    dfn[x]=low[x]=++dfs;
    for(int i=h[x];i;i=nxt[i])
    {
        if(to[i]==f)continue;
        if(!dfn[to[i]])
        {
            st[++top]=i;
            tarjan(to[i],x);
            low[x]=min(low[x],low[to[i]]);
            if(f==0)ch++;
            if(low[to[i]]>=dfn[x])
            {
                is[x]=1;
                tot++;
                while(1)
                {
                    if(used[from[st[top]]]!=tot)used[from[st[top]]]=tot,v[tot].push_back(from[st[top]]);
                    if(used[to[st[top]]]!=tot)used[to[st[top]]]=tot,v[tot].push_back(to[st[top]]);
                    if(st[top]==i)break;
                    top--;
                }
                top--;
            }
        }
        else if(dfn[to[i]]<dfn[x])st[++top]=i,low[x]=min(low[x],dfn[to[i]]);
    }
}