统计学习基本理论知识

Posted 2020-09-26 gaoshoufenmu

本篇将依据《统计自然语言处理》（宗成庆），重新梳理统计学习相关理论知识，相关概率论与梳理统计的课本不再列出来，可以找任意相关的课本复（预）习。

概率

概率是表示事件发生的可能性，将随机试验中的事件映射到实数域。用$P(A)$表示事件A的概率，$\\Omega$表示试验的样本空间（所有可能发生的事件），则概率满足：

1. 非负性：$P(A) \\geq 0$
2. 规范性：$P(\\Omega) = 1$
3. 可列可加性：对于可列个事件$A_1,A_2,...$，如果事件两两互不相容($A_i \\bigcap A_j = \\varnothing,  \\forall i \\neq j$)，则有$P(\\bigcup_{i} A_i) = \\sum_{i} P(A_i)$

独立

事件A 和B独立等价于$P(AB)=P(A)P(B)$

条件概率

$$P(A|B) = \\frac {P(A \\bigcap B)} {P(B)} $$

$$P(A \\bigcap B) = P(B)P(A|B) = P(A)P(B|A) $$

一般地，

$$P(A_1 \\bigcap \\cdot \\cdot \\cdot \\bigcap A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1 \\bigcap A_2) \\cdot \\cdot \\cdot P(A_n|A_1 \\bigcap A_2 \\bigcap \\cdot \\cdot \\cdot A_{n-1})$$

条件概率同样具有概率的三个性质

1. 非负性：$P(A|B) \\geq 0$
2. 规范性：$P(\\Omega | B) = 1$
3. 可列可加性：如果事件$A_1,A_2,...$两两不相容，则$P(\\sum_{i} A_i | B) = \\sum_{i} P(A_i | B)$

条件独立

如果$A_1,A_2$关于B条件独立，当且仅当$P(A_1,A_2 |B)=P(A_1 | B)P(A_2 | B)$

贝叶斯法则

根据条件概率有

$P(B|A)=\\frac {P(BA)} {P(A)} = \\frac {P(A|B)P(B)} {P(A)}$

比如应用贝叶斯理论到分类问题中，假设要求已知一个特征A发生的条件下，分类为B的概率，则可以统计样本中特征A出现的频率（用来估计$P(A)$），并统计样本中分类为B的那些样本中特征为A的频率（用来估计$P(A|B)$），于是分别计算特征A的条件下各个分类的条件概率，值最大的那个分类就是最终特征A所属的分类，而计算这些条件概率时，P(A)可以看作常数，所以

$$arg \\max_{B} \\frac {P(A|B)P(B)} {P(A)} = arg \\max_{B} P(A|B)P(B) $$

 

根据乘法规则，

$$P(A \\bigcap B) = P(A|B)P(B)$$

$$P(A \\bigcap \\overline B) = P(A| \\overline B)P(\\overline B)$$

于是有，

$$P(A) = P(A \\bigcap B) + P(A \\bigcap \\overline B) = P(A|B)P(B) + P(A| \\overline B)P(\\overline B) $$

一般地，假设B是样本空间$\\Omega$的一个划分，$\\sum_{i} B_i = \\Omega$，如果$A \\subseteq \\Omega$，即$A=\\sum_{i} AB_i$，那么

$$P(A) = \\sum_{i} P(AB_i) = \\sum_{i} P(A|B_i)P(B_i)$$

上式称为全概率公式

如果$P(A) > 0$，那么

$$P(B_j | A) = \\frac {P(A|B_j)P(B_j)} {P(A)} = \\frac {P(A|B_j)P(B_j)} {\\sum_{i} P(A|B_i)P(B_i)} $$

联合概率分布和条件概率分布

$(X_1,X_2)$是一个二维离散随机向量（约定大写表示随机变量，小写为随机变量的一个取值），则联合概率分布

$$p_{ij} = P(X_1=a_i,X_2=b_j) $$

条件概率分布为

$$P(X_1 = a_i | X_2 = b_j) = \\frac {P(X_1=a_i,X_2=b_j)} {P(X_2=b_j)} = \\frac {p_{ij}} {P(X_2=b_j)} $$

由于$P(X_2=b_j) = \\sum_{k} p_{kj}$，于是

$$P(X_1 = a_i | X_2 = b_j) = \\frac {p_{ij}} {\\sum_{k} p_{kj}} $$

$$P( X_2 = b_j | X_1 = a_i) = \\frac {p_{ij}} {\\sum_{k} p_{ik}} $$

贝叶斯决策理论

假设研究的分类有 c 个类别，各类别状态用$w_i$表示，各类别出现的先验概率为$P(w_i)$，特征空间的某一向量$\\vec x = [x_1, x_2, ..., x_d]^T$，维度为 d，且条件概率密度 $p(\\vec x|w_i)$是已知的（分类为$w_i$的样本中，特征向量等于$\\vec x$占比），于是利用贝叶斯公式得到后验概率，

$$p(w_i | \\vec x) = \\frac {p(\\vec x | w_i)p(w_i)} {\\sum_{j=1}^c p(\\vec x | w_j)p(w_j)}$$

如果$p(w_i| \\vec x) = \\max_{j=1,2,...,c} p(w_j|\\vec x)$，那么，$\\vec x \\in w_i$

因为后验概率右端分母为$p(\\vec x)$可以看作常数，所以

如果$p(\\vec x|w_i)p(w_i) = \\max_{j=1,2,...,c} p(\\vec x| w_j)p(w_j)$，那么，$\\vec x \\in w_i$

 期望和方差

随机变量X的概率分布为$P(X=x_k)= p_k$，若级数$\\sum_{k} x_k p_k$绝对收敛，则X的数学期望或者概率平均值为

$$E(X)=\\sum_{k} x_k p_k$$

方差为

$$var(X) = E((X-E(X))^2) = E(X^2) - E^2 (X) $$

标准差为$\\sqrt {var(X)}$

熵

随机变量X的概率分布为$p(x) = P(X=x)$，则熵（也称自信息）定义为

$$H(X) = - \\sum p(x)log_{2} p(x)$$

约定$0 log 0 = 0$

 联合熵和条件熵

联合熵

$$H(X,Y) = - \\sum{x \\in X} \\sum_{y \\in Y} p(x,y) log p(x,y)$$

条件熵

\\begin{aligned} H(Y|X) & = \\sum_{x \\in X} p(x) H(Y|X = x)  \\\\ & = \\sum_{x \\in X} p(x) [- \\sum_{y \\in Y} p(y|x) log p(y|x)] \\\\ & = - \\sum_{x \\in X} \\sum_{y \\in Y} p(x,y) log p(y|x) \\end{aligned}

将联合熵公式中的$logp(x,y)$ 展开，得

\\begin{aligned} H(X,Y) = - \\sum{x \\in X} \\sum_{y \\in Y} p(x,y) log p(x,y) \\\\ & =  - \\sum_{x \\in X} \\sum_{y \\in Y} p(x,y) log[p(x)p(y|x)] \\\\ & = - \\sum_{x \\in X} \\sum_{y \\in Y} p(x,y) log p(x) - \\sum_{x \\in X} \\sum_{y \\in Y} p(x,y) logp(y|x) \\\\ & = -\\sum_{x \\in X} p(x)log p(x) + H(Y|X) \\\\ & = H(X) + H(Y|X) \\end{aligned}

一般地，

$$H(X_1,X_2,...,X_n) = H(X_1) + H(X_2|X_1) + ... + H(X_n|X_1,X_2,...,X_{n-1})$$

互信息

根据熵的连锁规则有

$$H(X,Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) $$

于是，

$$H(X) - H(X|Y) = H(Y) - H(Y|X)$$

这个差就是X和Y的互信息，记作$I(X;Y)$，反应了知道Y值后X的不确定性的减少量，或者说Y的值透露了多少关于X的信息量，如下图

 

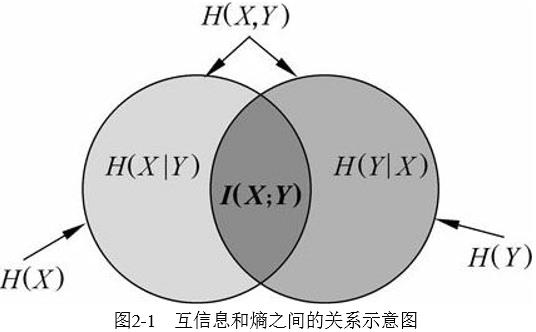
\\begin{aligned} I(X;Y) & = H(X) - H(X|Y) \\\\ & = H(X) + H(Y) - H(X,Y) \\\\ & = - \\sum_{x}p(x)log p(x) - \\sum_{y} p(y) log p(y) + \\sum_{x,y} p(x,y) log p(x,y) \\\\ & = - \\sum_{x,y} p(x,y) log p(x) - \\sum_{x,y} p(x,y) log p(y) + \\sum_{x,y} p(x,y) log p(x,y) \\\\ & = \\sum_{x,y} p(x,y) log {\\frac {p(x,y)} {p(x)p(y)}} \\end{aligned}

由于$H(X|X) = 0$，所以

$$H(X) = H(X) - H(X|X) = I(X;X) $$

条件互信息

$$I(X;Y|Z)=H(X|Z) - H(X|Y,Z)$$

向量互信息

$$I(X_{1n};Y)=I(X_1;Y) + I(X_2;Y|X_1) + I(X_n;Y|X_1,X_2,...,X_{n-1}) = \\sum_{i=1}^n I(X_i;Y|X_1,...,X_{i-1})$$

相对熵

两个概率分布$p(x),q(x)$的相对熵定义为（这里$p(x),q(x)$是两个相同事件空间里的概率分布，比如$p(x)$是真实概率分布，$q(x)$模型的概率分布即非真实分布，用来估计真实概率分布的），

$$D(p||q) = \\sum_{x \\in X} p(x) log {\\frac {p(x)} {q(x)}} $$

约定$0 log(0/q) = 0$，$p log(p/0) = $

相对熵可以看作是$log{\\frac {p(X)} {q(X)}}$的期望，

$$D(p||q) = E_{p}(log{\\frac {p(X)} {q(X)}})$$

显然，相对熵表示两个概率分布的差距的测度，当$p=q$时，$D(p||q)=0$

互信息就是联合分布与独立性差距的测度，

$$I(X;Y)=D[p(x,y) || p(x)q(x)] $$

证明：

\\begin{aligned} I(X;Y) & = H(X) - H(X|Y) \\\\ & = - \\sum_{x \\in X} p(x) log p(x) + \\sum_{x \\in X} \\sum_{y \\in Y} p(x,y) log p(x|y) \\\\ & = \\sum_{x \\in X} \\sum_{y \\in Y} p(x,y) log {\\frac {p(x|y} {p(x)}} \\\\ & = \\sum_{x \\in X} \\sum_{y \\in Y} p(x,y) log {\\frac {p(x,y)} {p(x)q(y)}} \\\\ & = D[p(x,y) || p(x)q(x)] \\end{aligned}

条件相对熵根据定义不难得到，

$$D[p(y|x)||q(y|x)]=\\sum_{x,y}p(x,y) log{\\frac {p(y|x)} {q(y|x)}} = \\sum_{x} p(x) \\sum_{y} p(y|x)  log{\\frac {p(y|x)} {q(y|x)}}$$

联合概率的相对熵为，

$$D[p(x,y) || q(x,y)] = D(p(x) || q(x)) + D[p(y|x) || q(y|x)]$$

证明：

\\begin{aligned} D[p(x,y) || q(x,y)] & = \\sum_{x,y} p(x,y) log { \\frac {p(x,y)} {q(x,y)} } \\\\ & = \\sum_{x,y} p(x,y) log { \\frac {p(x) p(y|x)} {q(x) q(y|x)} } \\\\ & = \\sum_{x,y} p(x,y) log { \\frac {p(x)} {q(x)}} + \\sum_{x,y} p(x,y) log { \\frac {p(y|x)} {q(y|x)}} \\\\ & = \\sum_{x} log{ \\frac {p(x)} {q(x)}} \\sum_{y} p(x,y) + D[p(y|x)||q(y|x)] \\\\ & = \\sum_{x} log{ \\frac {p(x)} {q(x)}} p(x) + D[p(y|x)||q(y|x)] \\\\ & = D(p(x) || q(x)) + D[p(y|x) || q(y|x)] \\end{aligned}

交叉熵

根据熵的定义，我们知道熵的本质是香农信息量$log{\\frac 1 {p(x)}}$的期望。

交叉这个词意味什么？想一想，然后我们给出交叉熵的定义，给出一个随机变量$X ~ p(x)$，$q(x)$为近似$p(x)$的概率分布，则随机变量X的真实分布p与模型（非真实分布）q之间的交叉熵为，

$$H(X,q) = H(p,q) = H(X) + D(p||q) = - \\sum_{x} p(x) log q(x) = E_{p} (log{\\frac 1 {q(x)}}) $$

 可以看出交叉熵是$log{\\frac 1 {q(x)}}$的期望，其中期望使用了真实概率分布$p(x)$，因为熵的计算用到了$p(x)$和$q(x)$，所以称为交叉熵。

我们知道熵$H(p) = - \\sum_{x} p(x) log p(x)$也可以用来表示平均编码长度，则交叉熵$H(p,q)$就是使用非真实分布 q 来计算平均编码长度，而$H(p,q) \\ge H(p)$，当q 为真实分布 p 时等号成立。

证明：

 我们使用拉格朗日乘子法来计算$H(p,q)$的极值，其中p是固定的，q是变量，当q = p 时，$H(p,q)$有极小值为$H(p)$，约束为$\\sum_{x} q(x) = 1$，拉格朗日函数为，

$$L = - \\sum_{x} p(x) logq(x) + \\lambda (\\sum_{x} q(x) - 1)$$

对$q(x)$求偏导并令其等于0，

$$\\frac {\\partial L} {\\partial q(x)} = - \\frac {p(x)} {q(x)} ln2 + \\lambda = 0 $$

注意，随便变量有多少个离散值x，就有多少个上式方程，变换一下，不难得到，

$$q(x) = p(x) \\frac {\\lambda} {ln 2}$$

对$\\lambda$求偏导并令其等于0，

$$\\sum_{x} q(x) - 1 = 0 $$

此即约束条件，于是

$$\\sum_{x} q(x) =  \\frac {\\lambda} {ln 2} \\sum_{x} p(x) =  \\frac {\\lambda} {ln 2} = 1$$

于是，

$$q(x) = p(x)$$

此时$H(p,q) =  - \\sum_{x} p(x) log q(x) = - \\sum_{x} p(x) log p(x) = H(p) $

上式表明q=p时，H(p,q)取极值H(p)，下面再证明是极小值即可。

对H(p,q)求二阶导得，

$$H(p,q)\' = - \\frac {p(x)} {q(x)} ln2$$

$$H(p,q)\'\' = \\frac {p(x)} {q^{2}(x)} ln2 $$

可见$H(p,q)\'\' \\ge 0$，即 $H(p,q)$是一个下凸函数，有极小值，于是$H(p,q) \\ge H(p)$得证。

上一小节中讲到的相对熵的概念也可以理解为使用非真实分布 q 得到的平均编码长度比使用真实分布 p 得到的平均编码长度多出的bit数：$D(p||q) = H(p,q) - H(p)$

语言模型

假设语言为L，语句是由单词组成的序列，即$W_{i}^n = (w_1,w_2,...w_n)$表示由n个单词组成的语句，那么基于语句的熵为

$$H(w_1,w_2,...w_n) = - \\sum_{W_{i}^n \\in L} p(W_{i}^n) log p(W_{i}^n) $$

平均每个单词的熵（entropy rate）为

$$\\frac 1 n H(w_1,w_2,...w_n) = - \\frac 1 n \\sum_{W_{i}^n \\in L} p(W_{i}^n) log p(W_{i}^n) $$

想要测量语言的真实熵，需要假设单词序列的长度很大，假设语言是产生一系列单词的随机过程L，其平均每个单词的熵（entropy rate）H(L)定义为，

$$H(L) = - \\lim_{n \\rightarrow \\infty} \\frac 1 n H(w_1,w_2,...w_n) = - \\lim_{n \\rightarrow \\infty} \\frac 1 n p(w_1,w_2,...w_n) log p(w_1,w_2,...w_n) $$

假设语言L 是稳态遍历的随机过程，根据Shannon-McMillan-Breiman理论有，

$$\\frac 1 n H(w_1,w_2,...w_n) = \\lim_{n \\rightarrow \\infty} - \\frac 1 n log p(w_1,w_2,...w_n) $$

定义语言L其模型q的交叉熵为

$$H(L,q) = - \\lim_{n \\rightarrow \\infty} \\frac 1 n \\sum_{W} p(w_1,w_2,...w_n) log q(w_1,w_2,...w_n) $$

其中，$p(w_1,w_2,...w_n)$表示语句出现的真实概率，$q(w_1,w_2,...w_n)$表示 模型q 对语句的概率估计。

再次根据Shannon-McMillan-Breiman理论，假设语言L 是稳态遍历的随机过程，则

$$H(L,q) = - \\lim_{n \\rightarrow \\infty} \\frac 1 n log q(w_1,w_2,...w_n)$$

困惑度

 设计语言模型时，通常用困惑度（perplexity）来代替交叉熵衡量语言模型的好坏。语言L中的单词序列$(w_1,w_2,...w_n)$，则语言的困惑度为

$$PP_{q} = 2^{H(L, q)} = 2^{- \\lim_{n \\rightarrow \\infty} \\frac 1 n log q(w_1,w_2,...w_n)} \\approx q(w_1,w_2,...w_n)^{- \\frac 1 n} $$

噪声信道模型

信息熵可以定量的估计信源每发送一个符号所提供的平均信息量。信号传输过程需要进行双重处理：1. 对编码进行压缩，尽量消除冗余。2. 由于信道有噪声，信道输出并不等于输入而是有一定信息的错误，所以需要通过增加一定的可控冗余以保障输入经过噪声信道后可以很好的恢复原样，这个可控冗余能检测和校验传输造成的错误。过程如下图

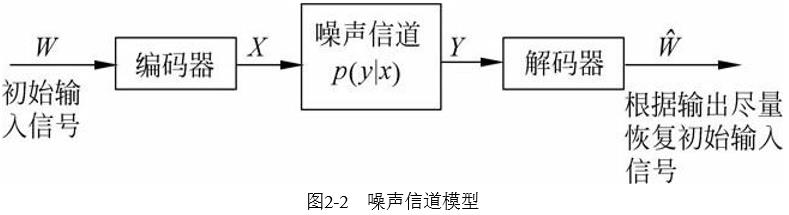
一个二进制对称信道的输入符号集为$X = \\lbrace 0, \\quad 1 \\rbrace$，输出符号集为$X = \\lbrace 0, \\quad 1 \\rbrace$。传输过程中如果符号被误传的概率为p，则正确传输的概率为 1- p，如下图

假设输入为X，输出为Y，如果Y很很好的逼近X，则信道的保真能力就很强，根据前面对互信息的介绍，我们定义信道容量为，

$$C = \\max_{p(X)} I(X;Y)$$

输入和输出的互信息达到最大值，这就是信道的最大传输容量

在自然语言处理中不需要编码，自然语言的句子可视为已编码的符号序列，但是需要解码，使观察到的输入序列更接近与输入，如下图，输入为I，经过信道输出为可观测序列O，解码得到原始输入$\\hat I$.

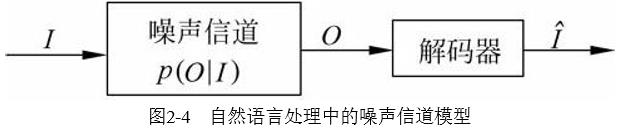
从所有可能的 I 中求解使得 p(O|I) 最大的那个I 认为是输入 $\\hat I$，根据贝叶斯公式，已知可观察的输出O的条件下，p(O)已经确定为一定值，

$$\\hat I = arg \\max_{I} p(I|O) = arg \\max_{I} \\frac {p(I)p(O|I)} {p(O)} = arg \\max_{I} p(I)p(O|I)$$

上式中，p(I)是语言模型，是指语言中 单词序列$(w_1,w_2,...w_n)$ 的概率分布，而 p(O|I)称为信道概率。例如，将一个法语句子 f 翻译成英语 e，那么翻译信道模型就是假设法语句子是观测到的输出 O，它原本的输入I 是一个英语句子 e，但通过噪声信号变成了法语句子 f，现在需要根据概率 p(e) 和 p(f|e) 计算求出最接近原始输入英语句子e 的解 $\\hat e$。