poj——3177Redundant Paths
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了poj——3177Redundant Paths相关的知识，希望对你有一定的参考价值。
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 15272 | Accepted: 6436 |
Description
Given a description of the current set of R (F-1 <= R <= 10,000) paths that each connect exactly two different fields, determine the minimum number of new paths (each of which connects exactly two fields) that must be built so that there are at least two separate routes between any pair of fields. Routes are considered separate if they use none of the same paths, even if they visit the same intermediate field along the way.
There might already be more than one paths between the same pair of fields, and you may also build a new path that connects the same fields as some other path.
Input
Lines 2..R+1: Each line contains two space-separated integers which are the fields at the endpoints of some path.
Output
Sample Input
7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
Sample Output
2
Hint
One visualization of the paths is:
1 2 3Building new paths from 1 to 6 and from 4 to 7 satisfies the conditions.
+---+---+
| |
| |
6 +---+---+ 4
/ 5
/
/
7 +
1 2 3Check some of the routes:
+---+---+
: | |
: | |
6 +---+---+ 4
/ 5 :
/ :
/ :
7 + - - - -
1 – 2: 1 –> 2 and 1 –> 6 –> 5 –> 2
1 – 4: 1 –> 2 –> 3 –> 4 and 1 –> 6 –> 5 –> 4
3 – 7: 3 –> 4 –> 7 and 3 –> 2 –> 5 –> 7
Every pair of fields is, in fact, connected by two routes.
It‘s possible that adding some other path will also solve the problem (like one from 6 to 7). Adding two paths, however, is the minimum.
Source
描述
为了从一个F（1＝f＝5000）放牧场（编号为1…F）到另一个场，Bessie和其他牧群被迫越过腐烂的苹果树附近。奶牛现在已经厌倦了常常被迫走一条特定的道路，并且想建立一些新的道路，这样他们就可以在任何一对田地之间选择至少两条独立的路线。他们目前至少有一对路线之间的每一对领域，并希望有至少两个。当然，当他们从一个领域迁移到另一个领域时，他们只能在正式的道路上旅行。
描述了R的电流设定（F-1 <= R <= 10000），每个连接两个不同领域的路径，确定新的路径的最小数目（每个连接两个领域），必须建立，至少有两个独立的路线，任何对田野之间。如果路径没有相同的路径，即使它们在同一个中间区域访问相同的路径，它们也被认为是独立的。
在同一对字段之间可能有不止一条路径，您还可以构建一个新路径，将同一字段与其他路径连接起来。
输入
第1行：两个空间分隔的整数：f和r
第2行…r + 1：每行包含两个空间分隔的整数，这是某个路径端点的字段。
输出
第1行：一个整数，这是必须建立的新路径的数量。
思路：
我们来考虑一下这道题的做法。
由于题目说，给定一张无向强连通图：判断至少需要加多少条边，使得任意两点之间至少有两条相互‘边独立’的道路，也就是说，至少加多少条边，使得这个图成为一个边双连通图。
什么是双连通图？！
双连通图分为两种：双边连通图与双点连通图，双边连通图就是不存在割边的连通图，点双联通图就是不存在割点的连通图。。（差不多是这样吧。。）
首先我们已经有了一个连通图，我们先判断这个强连通图中是否存在环，这个就与tarjan缩点（有向图时有一点差别了）这个图保证是一个强连通图，如果我们还按以前那样缩点的话，我们只会把这个图个缩成一个点，这样肯定不对啊。。。
我们在缩完点以后把它变成了一个树，这样我们只需要把它的子节点连通起来就好了
也就是说：加入的边的条数一定等于：（叶子节点数+1)/2
我们在这个地方所说的叶子结点为入读或出度为0的点。
但在这里我又想到令一种算法：我们可以先求割边，割边的条数就是我们要求的叶子结点的个数
这样说有人可能会不明白了，那好，我们来看一个图
对于这个图来说，我们先将这个图中存在的环缩成一个点，那它就变成了右图的样子
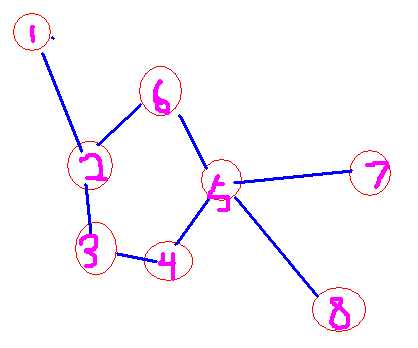在这里，我们以环缩点后的点5为根节点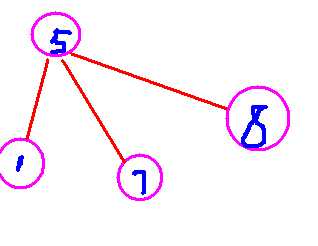 
看这个图的子节点是不是3？！
我们下面再来看看这个图的割边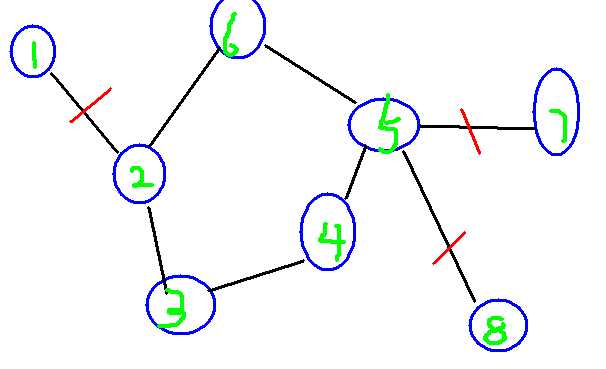
各大佬应该都能看出来我用红线割掉的边是这个图的割边吧。
他割边的个数是不是也是三？！ 也就是说我们上面的结论成立。
那么这个题就变成一个很裸的求割边的板子了。。
好我们来看看代码吧。。
代码：（然而这个思路只能得63分，为什么？！）我们来考虑一下上面的思路的错误所在。
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #define N 5005 using namespace std; bool vis[N][N]; long long n,m,x,y,ans,tot=1,tim; long long dfn[N],low[N]; long long head[20010],cut_edge[20010]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) {if(ch==‘-‘) f=-1; ch=getchar();} while(ch<=‘9‘&&ch>=‘0‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } struct Edge { int from,next,to; }edge[20010]; void add(int x,int y) { tot++; edge[tot].to=y; edge[tot].next=head[x]; head[x]=tot; } int tarjan(int now,int pre) { int sum=0; dfn[now]=low[now]=++tim; for(int i=head[now];i;i=edge[i].next) { if(i==(1^pre)) continue; int t=edge[i].to; if(!dfn[t]) { tarjan(t,i); low[now]=min(low[now],low[t]); if(low[t]>dfn[now]) cut_edge[i/2]=1; } else low[now]=min(low[now],dfn[t]); } } int main() { n=read(),m=read(); for(int i=1;i<=m;i++) { x=read(),y=read(); if(!vis[x][y]&&!vis[y][x]) add(x,y),add(y,x); vis[x][y]=vis[y][x]=true; } tarjan(1,0); for(int i=1;i<=m;i++) if(cut_edge[i]==1) ans++; ///printf("%d\\n",ans); printf("%d",(ans+1)>>1); return 0; }
样例的图有些不是很明显，我们来看另一个图
对于这样一个图的话：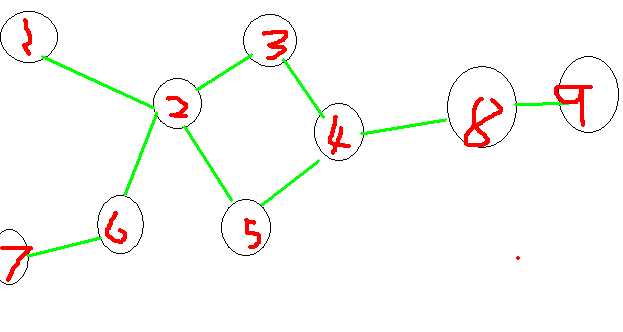
我们缩点之后把它变成了这样一个图：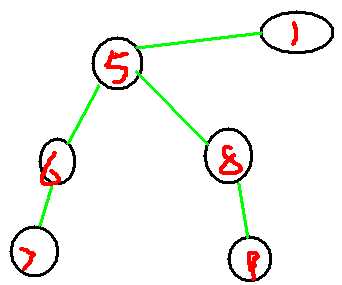
这个图割边的条数为：5条，如果按照我们刚刚的结论来看的话，我们要添3条边，然而我们只需要添2条边就可以了
为什么？！
看这个图：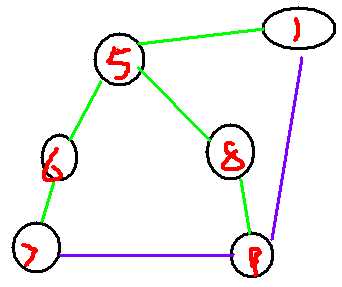
我们只需要在7~9，1~9之间添一条边就可以了。
那么我们还是乖乖地统计入读为2的点的个数吧。。。。。。（其实这个地方应该是度数为一的点，但是这个地方由于我们建的是双向边，每一个点都会统计两次，所以这个地方最小的将会是入读为2）
这个地方肯定有人就会问这样一个问题：为什么这个地方建的是双向边我们还能用tarjan缩点啊？！ 缩点的时候所得不是一个强连通分量吗？？这样的一个绝对联通的无向图不就是直接把他缩成了一个点了吗？！这样怎么还能这样做？！
想一下这个地方我们在缩点的时候为什么可以用tarjan？？
这样缩点主要是归功于这一句话：if(i==(1^pre)) continue; 对，他是用两条边，但是我们这个地方只让他走一条边，这样不就和有向图缩点一样了吗？！
代码：
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #define N 5005 using namespace std; bool vis[N]; long long n,m,x,y,ans,tot=1,tim,sum,top; long long du[N],dfn[N],low[N],stack[N],belong[N]; long long head[20010]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) {if(ch==‘-‘) f=-1; ch=getchar();} while(ch<=‘9‘&&ch>=‘0‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } struct Edge { int from,next,to; }edge[20010]; void add(int x,int y) { tot++; edge[tot].to=y; edge[tot].next=head[x]; head[x]=tot; } int tarjan(int now,int pre) { dfn[now]=low[now]=++tim; stack[++top]=now; for(int i=head[now];i;i=edge[i].next) { int t=edge[i].to; if(i==(1^pre)) continue; if(!dfn[t]) tarjan(t,i),low[now]=min(low[now],low[t]); else low[now]=min(low[now],dfn[t]); } if(low[now]==dfn[now]) { sum++; belong[now]=sum; for(;stack[top]!=now;top--) belong[stack[top]]=sum; top--; } } int main() { n=read(),m=read(); for(int i=1;i<=m;i++) x=read(),y=read(),add(x,y),add(y,x); tarjan(1,0); for(int i=1;i<=n;i++) for(int j=head[i];j;j=edge[j].next) if(belong[i]!=belong[edge[j].to]) du[belong[i]]++,du[belong[edge[j].to]]++; for(int i=1;i<=n;i++) if(du[i]==2) ans++; printf("%d",(ans+1)>>1); return 0; }
输入样例： 输出：32
200 250 1 3 106 1 134 1 157 134 23 106 60 134 44 60 117 1 126 1 11 134 139 44 178 3 97 60 101 157 118 44 30 23 128 30 174 3 108 23 110 128 132 157 92 106 173 132 79 106 82 178 7 44 52 79 74 30 4 23 49 7 164 139 127 30 156 4 65 7 120 101 46 97 112 178 8 46 59 60 198 174 100 134 90 92 192 60 125 100 26 178 19 192 63 125 155 126 70 100 35 63 151 126 165 157 146 70 84 157 141 52 160 70 163 8 38 127 171 139 62 101 133 11 177 146 158 125 41 165 145 52 98 30 5 177 68 164 168 173 107 178 86 132 199 127 136 168 71 155 50 128 189 35 193 46 105 70 195 189 89 158 69 177 190 50 28 19 21 92 93 71 170 86 122 21 131 136 197 158 16 108 33 195 18 164 196 141 94 92 61 79 149 26 169 193 124 163 78 189 147 108 150 49 129 70 77 168 194 18 54 100 140 127 24 196 109 158 2 97 17 195 64 28 115 174 185 41 81 141 45 62 180 18 167 109 27 65 123 140 188 77 91 129 73 110 76 173 14 149 103 105 51 11 57 84 58 101 148 193 43 156 162 109 22 61 179 52 67 74 200 117 6 167 119 192 113 41 184 16 32 98 39 160 75 32 175 98 121 78 183 26 47 174 102 79 83 23 172 127 176 74 138 121 182 90 29 156 153 183 114 162 152 47 15 136 12 64 143 155 161 89 99 90 87 114 25 193 144 86 137 64 135 52 56 14 55 112 20 71 142 5 34 126 116 56 40 79 130 89 187 49 85 62 111 136 191 39 166 16 159 120 13 50 95 55 154 33 96 171 181 115 88 21 80 24 48 14 72 21 31 67 9 31 66 143 37 117 104 56 36 86 42 125 186 33 10 184 53 18 164 64 136 63 77 25 128 105 133 147 130 1 67 161 10 132 190 173 195 80 123 1 70 82 126 38 163 7 193 17 152 105 44 24 168 185 174 163 177 40 79 173 70 19 26 60 198 130 97 22 143 67 97 25 119 89 194 163 188 180 49 173 109 71 4 124 58 79 151 178 74 93 34 96 161 65 167 16 172 114 183 14 46 116 199 187 118 175 109 23 101 115 160 114 110 173 96 28 77 182 27 116
以上是关于poj——3177Redundant Paths的主要内容，如果未能解决你的问题，请参考以下文章
POJ3177:Redundant Paths（并查集+桥）