粒子群优化算法和多模态优化算法有啥区别

Posted 2023-05-08

参考技术A 摘 要：，粒子群算法据自己的速度来决定搜索过程，只有最优的粒子把信息给予其他的粒子，整个搜索更新过程是跟随当前最优解的过程，所有的粒子还可以更快的收敛于最优解。由于微粒群算法简单，容易实现，与其它求解约束优化问题的方法相比较，具有一定的优势。实验结果表明，对于无约束的非线性求解，粒子群算法表现出较好的收敛性和健壮性。
关键词：粒子群算法；函数优化；极值寻优
0 引言
非线性方程的求根问题是多年来数学家努力解决的问题之一。长期以来，人们已找出多种用于解决方程求根的方法，例如牛顿法、弦割法、抛物线法等。然而，很多传统的方法仅能运用于相应的小的问题集，推广性相对较差。对于一个现实世界中的优化问题，必须尝试很多不同的方法，甚至要发明相应的新的方法来解决，这显然是不现实的。我们需要另外的方法来克服这样的困难。
粒子群算法是一种现代启发式算法，具有推广性强、鲁棒性高等特点[1]。该算法具有群体智能、内在并行性、迭代格式简单、可快速收敛到最优解所在区域等优点[2]。本文采用粒子群算法，对函数的极值进行寻优计算，实现了对函数的极值求解。
1 粒子群算法
1.1 基本原理
粒子群算法（PSO）是一种基于群体的随机优化技术，它的思想来源于对鸟群捕食行为的研究与模拟。粒子群算法与其它基于群体的进化算法相类似，选用“群体”和“进化”的概念，按照个体的适应度值进行操作，也是一种基于迭代的寻优技术。区别在于，粒子群算法中没有交叉变异等进化算子，而是将每个个体看作搜索空间中的微粒，每个微粒没有重量和体积，但都有自己的位置向量、速度向量和适应度值。所有微粒以一定的速度飞行于搜索空间中，其中的飞行速度是由个体飞行经验和群体的飞行经验动态调整，通过追踪当前搜索到的最优值来寻找全局最优值。
1.2 参数选择
粒子群算法需要修改的参数很少，但对参数的选择却十分敏感。El-Gallad A, El-Hawary M, Sallam A, Kalas A[3]主要对算法中的种群规模、迭代次数和粒子速度的选择方法进行了详细分析，利用统计方法对约束优化问题的求解论证了这 3 个参数对算法性能的影响，并给出了具有一定通用性的3 个参数选择原则[4]。
种群规模：通常根据待优化问题的复杂程度确定。
最大速度：决定粒子在一次迭代中的最大移动距离,通常设定为不超过粒子的范围宽度。
加速常数：加速常数c1和c2通常是由经验值决定的，它代表粒子向pbest和gbest靠拢的加速项的权重。一般取值为：c1=c2=2。
中止条件：达到最大迭代次数或得到最小误差要求，通常要由具体问题确定。
惯性权重：惯性权重能够针对待优化问题调整算法的局部和全局搜索能力。当该值较大时有利于全局搜索，较小时有利于局部搜索。所以通常在算法开始时设置较大的惯性权重，以便扩大搜索范围、加快收敛。而随着迭代次数的增加逐渐减小惯性权重的值，使其进行精确搜索，避免跳过最优解。
1.3 算法步骤
PSO算法步骤如下：
Step1：初始化一个规模为 m 的粒子群，设定初始位置和速度。
初始化过程如下：
（1）设定群体规模m;
（2）对任意的i，s，在[-xmax, xmax]内均匀分布，产生初始位置xis；
（3）对任意的i，s，在[-vmax, vmax]内均匀分布，产生速度vis；
（4）对任意的i，设yi=xi，保存个体。
Step2：计算每个粒子的适应度值。
Step3：对每个粒子的适应度值和得到过的最好位置pis的适应度值进行比较，若相对较好，则将其作为当前的最好位置。
Step4：对每个粒子的适应度值和全局得到过的最好位置pgs的适应度值进行比较，若相对较好，则将其作为当前的全局最好位置。
Step5：分别对粒子的所在位置和速度进行更新。
Step6：如果满足终止条件，则输出最优解；否则，返回Step2。
1.4 粒子群算法函数极值求解
粒子群算法优化是计算机智能领域，除蚁群算法外的另一种基于群体智能的优化算法。粒子群算法是一种群体智能的烟花计算技术。与遗传算法相比，粒子群算法没有遗传算法的选择（Selection）、交叉（Crossover）、变异（Mutation）等操作，而是通过粒子在解空间追随最优的粒子进行搜索。
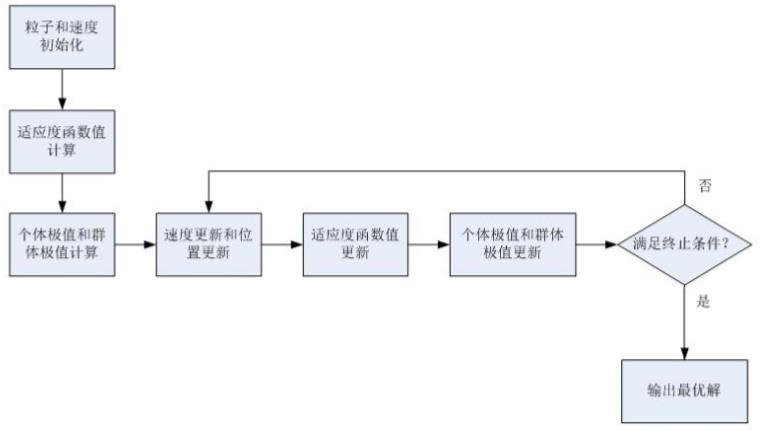
粒子群算法流程如图所示：

粒子群为由n个粒子组成的种群X = (X1,X2,X3,…Xn).
第i个粒子表示一个D维向量Xi = (X1,X2,X3,…XD)T.
第i个粒子的速度为Vi = (Vi1,Vi2,Vi3,…ViD)T.
个体极值为Pi = (Pi1,Pi2,Pi3,…PiD)T.
全局极值为Pg = (Pg1,Pg2,Pg3,…PgD)T.
速度更新为，式中，c1和c2为其两个学习因子的参数值；r1和r2为其两个随机值。
位置更新为.
2 粒子群算法应用举例
2.1 实验问题
这是一个无约束函数的极值寻优，对于Ackley函数，
.
其中c1=20，e=2. 71289。
2.2 实验步骤
对于Ackley函数图形，选取一个凹峰进行分析，程序运行结果如图所示。

图1 Ackley函数图形
可以看出，选取区间内的Ackley函数图形只有一个极小值点。因此，对于该段函数进行寻优，不会陷入局部最小。采用粒子群算法对该函数进行极值寻优。
首先，进行初始化粒子群，编写的MATLAB代码如下：
% 初始化种群
for i=1:sizepop
x1 = popmin1 (popmax1-popmin1)*rand;
% 产生随机个体
x2 = popmin2 (popmax2-popmin2)*rand;
pop(i,1) = x1; % 保存产生的随机个体
pop(i,2) = x2;
fitness(i) = fun([x1,x2]); % 适应度值
V(i,1) = 0; % 初始化粒子速度
V(i,2) = 0;
end
程序运行后所产生的个体值为：
表1 函数个体值

然后，根据待寻优的目标函数，计算适应度值。待寻优的目标函数为：
function y = fun(x)
y=-20*exp(-0.2*sqrt((x(1)^2x(2)^2)/2))-exp((cos(2*pi*x(1)) cos(2*pi*x(2)))/2) 20 2.71289;
根据每一组个体，通过目标函数，得到的适应度值为：

表2 函数适应度值

搜索个体最优极值，即搜索最小的适应度值，我们可利用MATLAB绘图将所有个体的适应度值绘成plot图查看相对最小值。

图3 函数适应度plot图
从图中可看出，当个体=20时，得到相对最小值，在程序中，将其保存下来。
之后进行迭代寻优，直到满足终止条件。
最后，得到的最优值为：

图4 MATLAB运行得到结果
迭代后得到的运行结果图如下：

图5 迭代曲线图
2.3 实验结果
通过图5中可看出，该函数的寻优是收敛的，最优个体和实际情况较吻合。因此，采用粒子群算法进行函数极值寻优，快速、准确且鲁棒性较好。
3 结论
本文阐述了粒子群算法求解最化问题的过程，实验结果表明了该算法对于无约束问题的可行性。与其它的进化算法相比，粒子群算法容易理解、编码简单、容易实现。但是参数的设置对于该算法的性能却有很大的影响，例如控制收敛，避免早熟等。在未来的工作中，将努力于将其它计算智能算法或其它优化技术应用于粒子群算法中，以进一步提高粒子群算法的性能。本回答被提问者采纳

粒子群优化算法PSO及matlab实现

 

算法学习自：MATLAB与机器学习教学视频

 

1、粒子群优化算法概述

粒子群优化（PSO, particle swarm optimization）算法是计算智能领域，除了蚁群算法，鱼群算法之外的一种群体智能的优化算法，该算法最早由Kennedy和Eberhart在1995年提出的，该算法源自对鸟类捕食问题的研究。
　　• PSO算法首先在可行解空间中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在最优解，用位置、速度和适应度值三项指标表示该粒子特征。
　　• 粒子在解空间中运动，通过跟踪个体极值Pbest和群体极值Gbest更新个体位置，个体极值Pbest是指个体所经历位置中计 算得到的适应度值最优位置，群体极值Gbest是指种群中的所有粒子搜索到的适应度最优位置。
　　• 粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体 极值Pbest和群体极值Gbest位置。

 

在每一次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，更新公式 如下：

　　　　　　　

　　　　　　

 

 2、粒子群优化算法与遗传算法对比

• 相同点：
　　种群随机初始化
　　适应度函数值与目标最优解之间的映射
• 不同点：
　　PSO算法没有选择、交叉、变异等操作算子
　　PSO有记忆的功能
　　信息共享机制不同，遗传算法是互相共享信息，整个种群的移动是比较均匀地向最优区域移动，而在PSO中，只 有gBest或lBest给出信息给其他粒子，属于单向的信息流动，整个搜索更新过程是跟随当前最优解的过程。因此， 在一般情况下，PSO的收敛速度更快。

 

3、案例分析

①一元函数优化

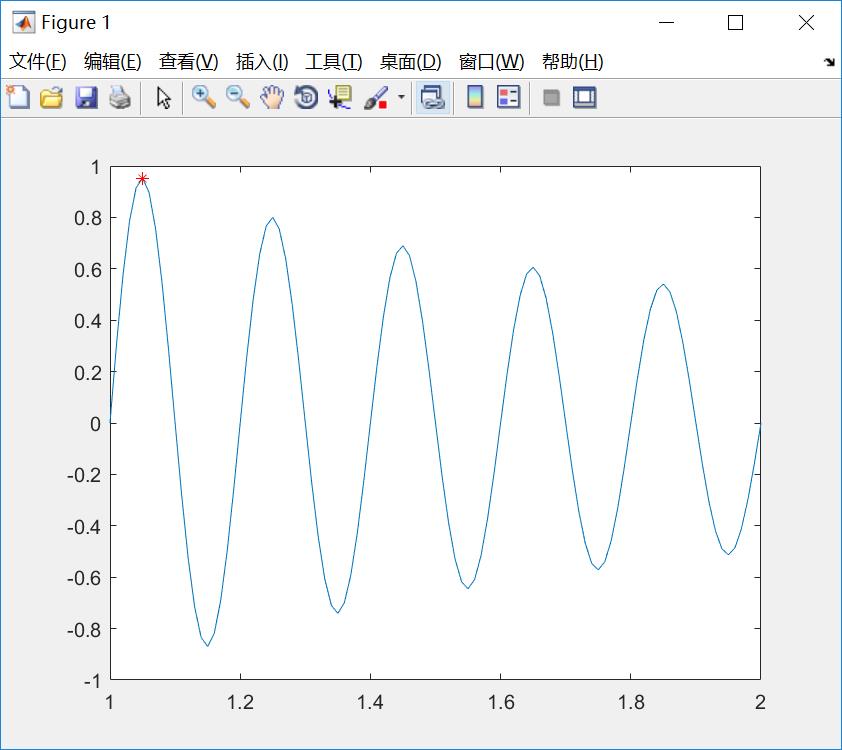
　　在该例中，想要优化的一元函数为，当x范围在[1,2]，寻找它的极大值。

matlab代码如下：

 1 %% I. 清空环境
 2 clc
 3 clear all
 4 
 5 %% II. 绘制目标函数曲线图
 6 x = 1:0.01:2;
 7 y = sin(10*pi*x) ./ x;
 8 figure
 9 plot(x, y)
10 hold on
11 
12 %% III. 参数初始化
13 c1 = 1.49445;
14 c2 = 1.49445;
15 
16 maxgen = 50;   % 进化次数  
17 sizepop = 10;   %种群规模
18 
19 Vmax = 0.5;
20 Vmin = -0.5;
21 popmax = 2;
22 popmin = 1;
23 
24 %% IV. 产生初始粒子和速度
25 for i = 1:sizepop
26     % 随机产生一个种群
27     pop(i,:) = (rands(1) + 1) / 2 + 1;    %初始种群
28     V(i,:) = 0.5 * rands(1);  %初始化速度
29     % 计算适应度
30     fitness(i) = fun(pop(i,:));   
31 end
32 
33 %% V. 个体极值和群体极值
34 [bestfitness, bestindex] = max(fitness);
35 zbest = pop(bestindex,:);   %全局最佳
36 gbest = pop;    %个体最佳
37 fitnessgbest = fitness;   %个体最佳适应度值
38 fitnesszbest = bestfitness;   %全局最佳适应度值
39 
40 %% VI. 迭代寻优
41 for i = 1:maxgen
42     
43     for j = 1:sizepop
44         % 速度更新
45         V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
46         V(j,V(j,:)>Vmax) = Vmax;
47         V(j,V(j,:)<Vmin) = Vmin;
48         
49         % 种群更新
50         pop(j,:) = pop(j,:) + V(j,:);
51         pop(j,pop(j,:)>popmax) = popmax;
52         pop(j,pop(j,:)<popmin) = popmin;
53         
54         % 适应度值更新
55         fitness(j) = fun(pop(j,:)); 
56     end
57     
58     for j = 1:sizepop    
59         % 个体最优更新
60         if fitness(j) > fitnessgbest(j)
61             gbest(j,:) = pop(j,:);
62             fitnessgbest(j) = fitness(j);
63         end
64         
65         % 群体最优更新
66         if fitness(j) > fitnesszbest
67             zbest = pop(j,:);
68             fitnesszbest = fitness(j);
69         end
70     end 
71     yy(i) = fitnesszbest;          
72 end
73 
74 %% VII. 输出结果并绘图
75 [fitnesszbest zbest];
76 plot(zbest, fitnesszbest,\'r*\')
77 
78 figure
79 plot(yy)
80 title(\'最优个体适应度\',\'fontsize\',12);
81 xlabel(\'进化代数\',\'fontsize\',12);ylabel(\'适应度\',\'fontsize\',12);

main.m

1 function y = fun(x)
2 % 函数用于计算粒子适应度值
3 %x           input           输入粒子 
4 %y           output          粒子适应度值 
5 y = sin(10 * pi * x) / x;

fun.m

 

结果图示：

2、二元函数优化

 　　在该例中，想要优化的二元函数为，当x和y范围都在[-5,5]，寻找它的极大值。

matlab代码如下：

1 function y = fun(x)
2 %函数用于计算粒子适应度值
3 %x           input           输入粒子 
4 %y           output          粒子适应度值 
5 y = x(1).^2 + x(2).^2 - 10*cos(2*pi*x(1)) - 10*cos(2*pi*x(2)) + 20;

fun.m

 1 %% I. 清空环境
 2 clc
 3 clear
 4 
 5 %% II. 绘制目标函数曲线
 6 figure
 7 [x,y] = meshgrid(-5:0.1:5,-5:0.1:5);
 8 z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
 9 mesh(x,y,z)
10 hold on
11 
12 %% III. 参数初始化
13 c1 = 1.49445;
14 c2 = 1.49445;
15 
16 maxgen = 1000;   % 进化次数  
17 sizepop = 100;   %种群规模
18 
19 Vmax = 1;
20 Vmin = -1;
21 popmax = 5;
22 popmin = -5;
23 
24 %% IV. 产生初始粒子和速度
25 for i = 1:sizepop
26     % 随机产生一个种群
27     pop(i,:) = 5*rands(1,2);    %初始种群
28     V(i,:) = rands(1,2);  %初始化速度
29     % 计算适应度
30     fitness(i) = fun(pop(i,:));   %染色体的适应度
31 end
32 
33 %% V. 个体极值和群体极值
34 [bestfitness bestindex] = max(fitness);
35 zbest = pop(bestindex,:);   %全局最佳
36 gbest = pop;    %个体最佳
37 fitnessgbest = fitness;   %个体最佳适应度值
38 fitnesszbest = bestfitness;   %全局最佳适应度值
39 
40 %% VI. 迭代寻优
41 for i = 1:maxgen
42     
43     for j = 1:sizepop
44         % 速度更新
45         V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
46         V(j,find(V(j,:)>Vmax)) = Vmax;
47         V(j,find(V(j,:)<Vmin)) = Vmin;
48         
49         % 种群更新
50         pop(j,:) = pop(j,:) + V(j,:);
51         pop(j,find(pop(j,:)>popmax)) = popmax;
52         pop(j,find(pop(j,:)<popmin)) = popmin;
53         
54         % 适应度值更新
55         fitness(j) = fun(pop(j,:)); 
56     end
57     
58     for j = 1:sizepop  
59         % 个体最优更新
60         if fitness(j) > fitnessgbest(j)
61             gbest(j,:) = pop(j,:);
62             fitnessgbest(j) = fitness(j);
63         end
64         
65         % 群体最优更新
66         if fitness(j) > fitnesszbest
67             zbest = pop(j,:);
68             fitnesszbest = fitness(j);
69         end
70     end 
71     yy(i) = fitnesszbest;            
72 end
73 %% VII.输出结果
74 [fitnesszbest, zbest]
75 plot3(zbest(1), zbest(2), fitnesszbest,\'bo\',\'linewidth\',1.5)
76 
77 figure
78 plot(yy)
79 title(\'最优个体适应度\',\'fontsize\',12);
80 xlabel(\'进化代数\',\'fontsize\',12);ylabel(\'适应度\',\'fontsize\',12);

main.m

 

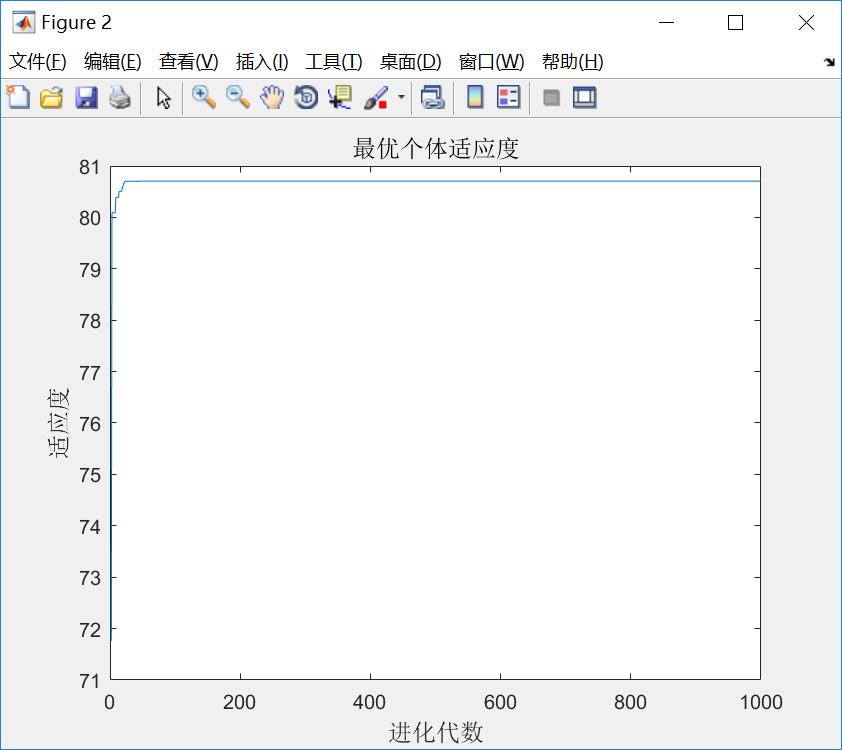
结果图示：

    

 

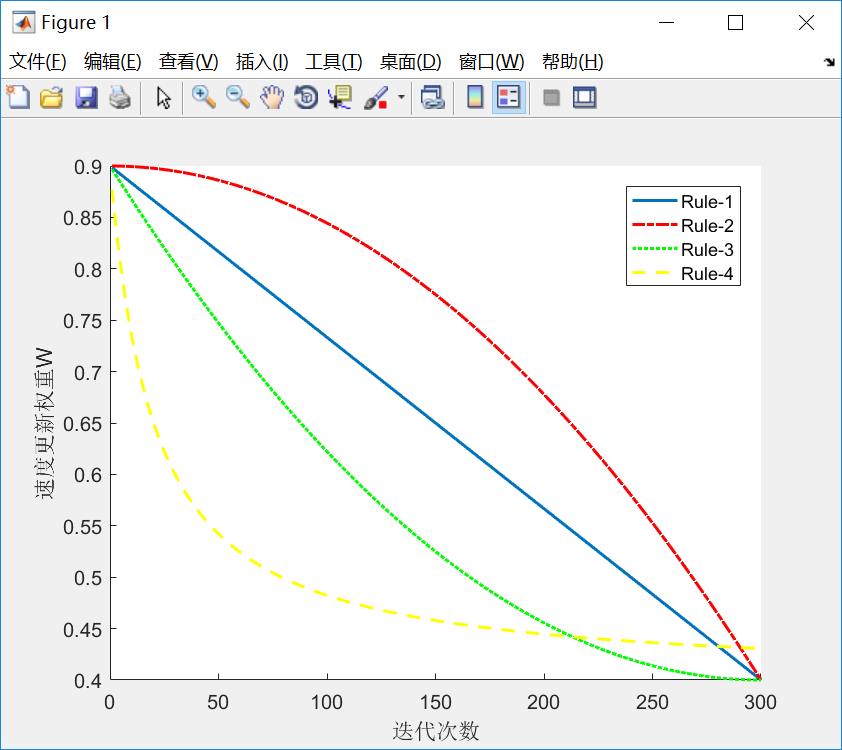
4、速度更新权重W的选择

 

 

示例代码如下：

 1 ws = 0.9;
 2 we = 0.4;
 3 maxgen = 300;
 4 hold on;
 5 
 6 for k = 1:maxgen
 7     w(k) = ws - (ws-we)*(k/maxgen);
 8 end
 9 plot(w,\'linewidth\',1.5);
10 
11 for k = 1:maxgen
12     w(k) = ws - (ws-we)*(k/maxgen)^2;
13 end
14 plot(w,\'r-.\',\'linewidth\',1.5);
15 
16 for k = 1:maxgen
17     w(k) = ws - (ws-we)*(2*k/maxgen-(k/maxgen)^2);
18 end
19 plot(w,\'g:\',\'linewidth\',1.5);
20 
21 for k = 1:maxgen
22     w(k) = we * (ws/we)^(1/(1+10*k/maxgen));
23 end
24 plot(w,\'y--\',\'linewidth\',1.5);
25 
26 legend(\'Rule-1\',\'Rule-2\',\'Rule-3\',\'Rule-4\')
27 xlabel(\'迭代次数\')
28 ylabel(\'速度更新权重W\')

wchange.m

图示：