名词解释 算法

Posted 2023-05-08

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。 参考技术A 5.1算法推送新闻的伦理现象成因
5.1.1 算法技术尚不成熟
目前人工智能技术尚弱，技术存在缺陷。虽然在与新闻业的融合过程中取得了显著成果，但也带来了伦理方面的问题。
人们对科学技术的大量投入体现了对人工智能充满期待，信息科学技术也确实实现了我们曾经向往的生活——信息传播跨越时空限制、实现即时更新传播。但是技术不是万能的，人工智能能够实现新闻自动化写作而无法像人类一样对自身合成的信息进行核查,缺少思辨意识和能力。另外，人工智能源于对人类智慧的模仿，涉及心理学、计算机科学等多种学科，而学科发展现状在很大程度上决定了人工智能的最终实现效果，其发展道路不是一帆风顺的，技术瓶颈期时而出现。
5.1.2 片面迎合新闻生产需要
新闻生产活动不是孤立的，而是关乎各个群体的利益，新闻传播产业为迎合市场需求，不断更新信息传播和呈现方式，从而吸引用户的持续关注。当技术发展到一定阶段就会在市场中转化为商业化模式。无论新闻业抑或是其他行业，应用人工智能的最后结果都将转化为商业价值。在商业与利益的驱使下，新闻生产主体为迎合用户的需求，利用人工智能进行大规模的新闻生产和传播，其中不免会存在损害公众利益的行为。
5.1.3 用户媒介素养欠缺
在互联网大环境下，受众的媒介素养参差不齐，人工智能技术引领的媒智化趋势也需要相应改变受众对新技术的观念，要理性看待技术红利背后的潜伏危机，媒介素养问题日益引起重视。面对复杂的传媒环境，受众的媒介素养在很大程度上决定媒介的发展方向
随着人工智能在传播领域的普及与应用，媒介素养贯穿算法新闻生产全过程，主要指人们对算法新闻信息的认知、理解和传播能力。根据麦克卢汉的媒介和讯息观点，媒介工具对社会的影响一直存在。人们对算法新闻的认识还不够全面，新奇大于忧虑，容易沉浸在算法新闻当中，这也是当下算法推送技术在新闻传播到各环节发挥作用的原因所在，算法热潮在不同的时期都会有不同形式的呈现，现阶段的算法新闻热潮迫切需要受众转变传统的媒介素养观念,学会用互联网思维从不同角度看待新生事物。
5.1.4 监管方面缺失
首先，算法新闻监管措施不到位，技术弊端没有得到有关部门的有效管控。人工智能应用于新闻传播行业所造成的新闻伦理问题和人工智能没有—套科学的监管体系。算法新闻是交叉学科领域，由于监管机构的审查不到位，造成算法决策的公开性和公平性难以得到保障,使得虚假新闻和低俗信息频频再现，更引发个人隐私问题暴露于公众视野等传播伦理失范行为。技术本身没有好坏之分，重点是在算法生产者如何管理和使用。社会亟需专业全面的人工智能技术监管机构和全媒体人才。
受众有权通过不同的途径来监督媒体组织的信息传播失范行为，保证受众监督途径畅通无阻也是完善人工智能市场监管机制的有效措施。其次，目前人工智能技术不具有独立思考和判断能力,而是完全受程序化控制。因此自我学习能力也是在原有的数据资源和模式化上设定，这样很容易在处理敏感新闻时把道德伦理置之不顾，损害公众利益。现阶段对于通过人工智能技术获取不正当利益的行为还没有明确的法律处罚，这样伦理失范事件时有发生。
5.2算法推送新闻的伦理问题应对策略[]
5.2.1 强化人机协作
如今技术的发展越来越快，人类的主体地位不可忽略，人类探索人工智能技术的初心也不能因为小小的困难而改变。在充满智能化的新闻生产中，新闻从业人员依旧会承担着关键作用，但技术的会不断发展和完善，人工智能在许多方面已经表现出超越人力所及的潜力，人们不禁陷入技术恐慌境地，渐渐越来越多的工作会被人工智能所取代，这时的人类将何去何从?技术乐观主义和悲观主义都有其存在的依据，我们不应过度沉溺于悲欢情感境遇当中，应当去思考人机之间的关系，去发挥人工智能技术的最大潜力，让其更好地为人类服务。
5.2.2 优化技术中介
首先，在使用范围和标准上，应规范人工智能技术的使用，处理好技术和内容的相互关系。技术对新闻内容的过滤虽然相比人类来说可能欠缺自我思考，但准确性更高，算法功能更多。它可以有统计分析归类，检索关键词，词语识别，对敏感词过滤，营造应该积极健康的信息环境。
个性化算法推送技术会造成受众深陷信息茧房，目前的市面上新闻推送软件基本是按照用户初次检索信息时输入的关键词和点击的信息的行为动作为用户推荐新闻，这种方式其实并没有考虑到用户的多维度信息需求，将用户与其他信息隔绝开来。但通过大数据技术可以将个人信息的进行深度融合，在新闻内容消费之外，我们的大量行为数据可以各种网络的方式被保留下来，这部分数据可以作为内容推送的参考和分析，同时也能成为新闻内容的原始数据扩充到海量数据库中，经过多次加工的新闻信息会将公众带入人为搭建好的拟态环境。然而，大范围数据信息记录和传播会增加个人隐私的暴露风险。人工智能技术的完善还需要时间和不断实践去摸索，媒体要在新闻生产各环节加强信息把关，对数据源进行严格把关，避免信息输入出现问题。
5.2.3 用户价值观与算法新闻价值观需彼此适应
算法新闻对新闻传播行业的影响波及新闻生产的整个过程，除了技术变革新闻生产结构外，也有对新闻价值观造成一定程度的冲击，算法推送技术呈现的新闻在保留传统新闻模式的同时也开发出不同于旧时代的新闻价值，受众对新闻内容和技术的认识都正在经历着新旧转换，我们需要重新考量算法新闻的新闻价值，调整受众对新闻信息接收失衡的状态。
杜骏飞在《Internet被解放的新闻价值观》中谈到：“首先作为传统新闻思想核心的、关于‘客观性’的价值，在网络环境下正在向‘客观-主观性’的综合型价值观方向发展。其次，传统的新闻价值系统中诸种较为公正的元素或指向，在泛传播的条件下，正由单调的偏倚而走向辩证的统合。”这些统合包括以下几种情况：异常性与寻常性的统合。影响信誉，交响性的统合。及时信誉全市性的统合，人情性与人群性的统合。
算法新闻开放式的新闻生产模式，给予了用户更多参与内容生产的机会。人工智能技术确实实现了一部分技术和情感的耦合。但人工智能依然对内容产品存在认知偏向。自动化新闻写作的数据完整性和真伪性是不能被机器有效识别的，因此算法新闻时代，虚假新闻的生产与传播未见减少，甚至有增加的迹象，助长了虚假新闻的辨识难度。再者，人工智能对数据信息的深度发掘对用户的隐私性带来不可磨灭的影响。技术尚存在许多弊端，受众和用户要理性看待算法新闻。
5.2.4 完善法规体系
加快立法体系的建设，其顶层设计尤为重要。需要注意的是，法律规制不能只是依靠立法者，也需要法律人才与技术人员的合作。—方面是要研究制定算法等网络技术的相关法律，使法治管理嵌入算法等网络技术的生产、设计和经营环节。另一方面是对于算法推荐技术等网络技术关联的相关法律概念的界定也需要同时推进，比如进—步明确隐私权等人权的权限边界和行为规范。同时需要密切关注算法推荐的技术创新发展，特别是其在政治、经济等领，域的运用和影响，在制定法律的时间差上不至于落后太多。

Adaboost算法的原理推导及解释

文章目录

• Adaboost算法的原理推导及解释
• • 前置知识：Boosting概述
  • • Boosting方法的基本思想
    • Boosting方法的的学习方法
  • 核心部分：Adaboost算法的原理推导和解释
  • • Adaboost算法的基本思想
    • Adaboost算法的算法流程

Adaboost算法的原理推导及解释

前置知识：Boosting概述

Boosting方法的基本思想

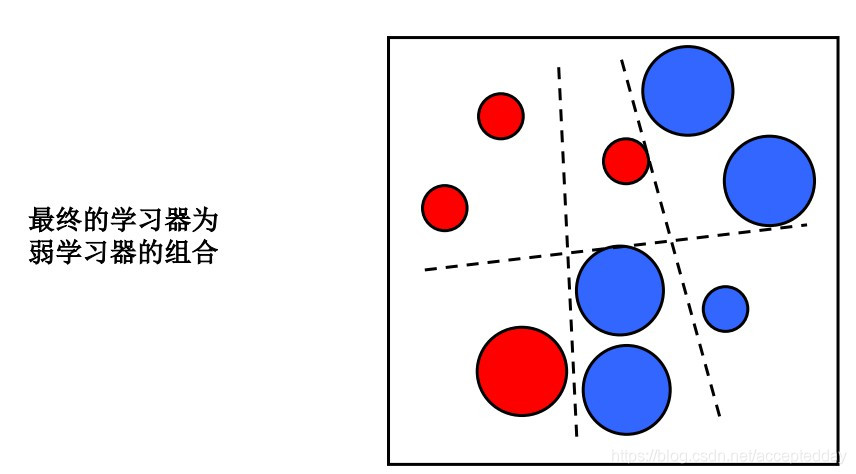
该方法使用迭代方式完成对各个弱学习器的训练构造， 每次迭代对训练样本集的选择都与前面各轮的学习结果有关。

使用前面各轮学习结果更新当前各训练样本的权重，对前面被错误预测的赋予较大的权重，实现对当前训练样本集合数据分布的优化。

Boosting方法的的学习方法

Boosting 集成学习通常使用两种方式调整训练样本集的数据分布。

• 仅调整样本数据的权重，而不改变当前训练样本集合。

• 改变当前训练样本集合，将被前面弱学习器错误预测的样本复制到关于当前弱学习器的训练样本集合中重新进行训练。

在实际的模型训练中，常使用第一种方式调整训练样本的数据分布。第二种方式是复制被前面弱学习器错误预测样本到样本训练集当中重新进行训练。

而调整样本权重的基本思想是提高当前训练样本集合中被错误预测样本的权重，降低已被正确预测样本的权重，使得后续对的弱学习器的训练构造更加重视那些被错误预测的样本。

关于权重的理解（非常重要！！！）：

• 一方面，指的是分类错误率方向的影响，指的是计算学习器L对样本集D的分类错误率时候的样本比重，即假如样本d_j分类错误，本来该样本权重系数应该是1/n（n为样本集D的样本总数目），然后经过调整，d_j的权重系数修改为1/2；相应的d_i分类正确的样本权重修改为1/2。

• 另一方面，指的是模型参数训练优化方向的影响，指的是模型不断优化的梯度或者决策方向，朝着哪一个或者哪些方向去迭代优化，例如：${\mathbf{w}}_{\mathbf{i}+1}={\mathbf{w}}_{\mathbf{i}}+{\sum }_{\mathbf{k}=1}^{\mathbf{n}}{\mathbf{w}}_{\mathbf{i}\mathbf{k}}\phi \left({\mathbf{w}}_{\mathbf{i}\mathbf{k}}{\mathbf{X}}_{\mathbf{k}}\right)$，当模型参数的更新公式中涉及到输入样本时，权重将会影响模型参数的优化方向。

方法的流程如下：

• 对于n个样本的训练集，初始样本权重为1/n，则对所有被预测错误样本集Q，其整体权重等于ε。
• 若规定权重更新后Q的整体权重为1/2,则需将其初始权重ε乘以1/(2ε), 即ε*1/(2ε)=1/2。
• 为了保证更新后的概率之和为1,则剩余样本应乘以1/[2(1-ε)]。

例题：现有均匀分配权重样本集训练得到的分类器𝐶1，其分类结果如表所示。试更新该训练样本集的权重并求出分类器𝐶1基于更新权重后样本集的分类错误率。

依题意可知，共有60个分类正确样本、共40个分类错误样本，分类错误率为𝜀 =0.4。错误分类样本权重更新因子𝛼 = 1/(2𝜀)= 1.25，正确分类样本权重更新因子𝛽 = 1/[2(1 − 𝜀)]=5/6，则权重更新后分类结果 表所示，此时错误率𝜀′ = 0.5，结果如下表。

核心部分：Adaboost算法的原理推导和解释

Adaboost算法的基本思想

AdaBoost是一种具有自适应性质的Boosting集成学习算法，自适应性主要表现在自动提升被错误预测样本的权重，自动减少被正确预测样本的权重，使得弱学习器训练过程能够根据模型预测性能自动进行调整。

Adaboost算法的算法流程

现以二分类任务为例介绍该算法的具体过程：

• 对于训练样本集𝐷 = 𝑋₁, 𝑦₁ , 𝑋₂, 𝑦₂ , ⋯ , (𝑋_𝑛, 𝑦_𝑛)，其中𝑦_𝑖𝜖−1, +1，由 AdaBoost 集成学习算法构造集成模型的基本步骤如下：

  （1）令𝑖=1并设定弱学习器的数目𝑚。使用均匀分布初始化训练样本集的权重分布，令𝑛维向量𝑤^𝑖表示第𝑖次需更新的样本权重，则有：𝑤¹= (𝑤₁₁, 𝑤₁₂, ⋯ , 𝑤_1𝑛)^𝑇 =(1/n, 1/n, …, 1/n)^T。 （w₁₂代表第1次迭代，第2个样本对应的样本权重，一个样本的权重主要影响的是模型不断优化的梯度或者决策方向，朝着哪一个或者哪些方向去迭代优化，例如：${\mathbf{w}}_{\mathbf{i}+1}={\mathbf{w}}_{\mathbf{i}}+{\sum }_{\mathbf{k}=1}^{\mathbf{n}}{\mathbf{w}}_{\mathbf{i}\mathbf{k}}\phi \left({\mathbf{w}}_{\mathbf{i}\mathbf{k}}{\mathbf{X}}_{\mathbf{k}}\right)$，当模型参数的更新公式中涉及到输入样本时，权重将会影响模型参数的优化方向）

  （2）使用权重分布为𝑤^𝑖的训练样本集𝐷_𝑖学习得到第𝑖个弱学习器𝑓_i 。

  （3）计算𝑓_𝑖在训练样本集𝐷_𝑖上的分类错误率𝑒_𝑖：
  $${\mathbf{e}}_{\mathbf{i}}=\sum _{\mathbf{k}=1}^{\mathbf{n}}{\mathbf{w}}_{\mathbf{i}\mathbf{k}}\mathbf{I}\left({\mathbf{f}}_{\mathbf{i}}\left({\mathbf{X}}_{\mathbf{k}}\right)\ne {\mathbf{y}}_{\mathbf{k}}\right)$$
  （4）确定弱学习器𝑓_𝑖的组合权重𝛼_𝑖。由于弱学习器𝑓_𝑖的权重取值应与其分类性能相关，对于分类错误率𝑒_𝑖越小的𝑓_𝑖，则其权重𝛼_𝑖应该越大，故有${\alpha }_{\mathbf{i}}=\frac{1}{2}\ln \frac{1-{\mathbf{e}}_{\mathbf{i}}}{{\mathbf{e}}_{\mathbf{i}}}$。

  （5）依据弱学习器𝑓_𝑖对训练样本集𝐷_𝑖的分类错误率𝑒_𝑖更新样本权重，更新公式为${\mathbf{w}}_{\mathbf{i}+1,\mathbf{j}}=\frac{{\mathbf{w}}_{\mathbf{i}\mathbf{j}}{\mathbf{e}}^{\left(-{\alpha }_{\mathbf{i}}{\mathbf{y}}_{\mathbf{j}}{\mathbf{f}}_{\mathbf{i}}\left({\mathbf{X}}_{\mathbf{j}}\right)\right)}}{{\mathbf{z}}_{\mathbf{i}}}$，其中为${\mathbf{z}}_{\mathbf{i}}={\sum }_{\mathbf{j}=1}^{\mathbf{n}}{\mathbf{w}}_{\mathbf{i}\mathbf{j}}{\mathbf{e}}^{\left(-{\alpha }_{\mathbf{i}}{\mathbf{y}}_{\mathbf{j}}{\mathbf{f}}_{\mathbf{i}}\left({\mathbf{X}}_{\mathbf{j}}\right)\right)}$归一化因子，保证更新后权重向量是概率之和等于1。（其中y_j∈1,-1，而f_i(X_j)∈1，-1，如果第i次迭代，分类正确，则相对之前的权重降低了$\sqrt{\frac{{\mathbf{e}}_{\mathbf{i}}}{1-{\mathbf{e}}_{\mathbf{i}}}}$；否则，权重则提升了$\sqrt{\frac{1}{{\mathbf{e}}_{\mathbf{i}}}-1}$。）

  （6）若𝑖 < 𝑚，则令𝑖 = 𝑖 + 1并返回步骤（2），否则执行步骤（7）。

  （7）对于𝑚个弱分类器𝑓₁, 𝑓₂, ⋯ , 𝑓_𝑚，分别将每个𝑓_𝑖按权重𝛼_𝑖进行组合： $\mathbf{G}=\mathbf{s}\mathbf{i}\mathbf{g}\mathbf{n}({\sum }_{Adaboost算法的原理推导及解释}$

  Adaboost算法的原理推导及解释

  解释一段Apriori算法的意思，越详细越好偶电脑白痴

  三维可视化名词解释-体绘制体素体数据体绘制算法

  EM算法的原理推导及解释

  EM算法的原理推导及解释