机器学习：Logistic回归原理及其实现

Posted 2020-09-25 Make Change

Logistic回归是机器学习中非常经典的一个方法，主要用于解决二分类问题，它是多分类问题softmax的基础，而softmax在深度学习中的网络后端做为常用的分类器，接下来我们将从原理和实现来阐述该算法的思想。

 

1.原理

a.问题描述

考虑二分类问题，利用回归的思想，拟合特征向量到类别标签的回归,从而将分类问题转化为回归问题，通常通过引入Logistic平滑函数实现。

假设已知训练样本集\\(D\\)的\\(n\\)个样本\\(\\{(x_{i},t_{i})| i=1,...,n\\}\\) ，其中\\(t_{i}\\in \\left \\{ 0,1 \\right \\}\\) 为类别标签，\\(x_{i} \\in R^{d}\\) 为特征向量。

b.Logistic函数

Logistic回归需要用到一个重要的Logistic函数，又称为Sigmod函数，Logistic的重要作用就是通过它建立了特征和类别概率的拟合关系，其形式如下：

\\(f\\left ( x \\right )=\\frac{1}{1+exp(-x)}\\)

对应的图如下所示：

 

 

 

 

 

 

 

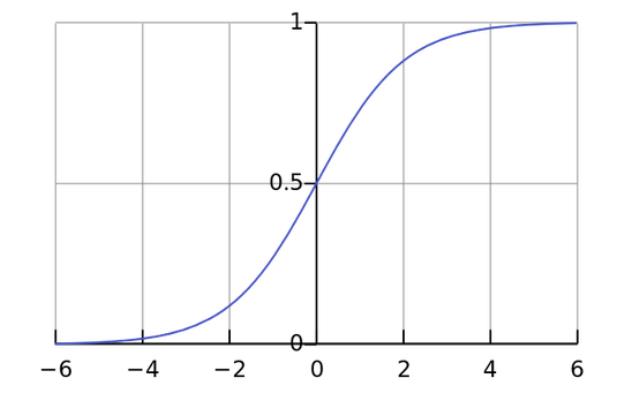
Logistic函数具有以下两个重要的性质：

i:    \\(f(-x)=1-f(x)\\)

ii:    \\({f}\'(x)=f(x)f(-x)=f(x)(1-f(x))\\)

c.目标函数

 根据Logistic函数，Logistic回归的回归函数为

\\(g(x)=\\frac{1}{1+exp(w^{\\mathit{T}}x)}\\)

其中\\(w\\) 为回归参数。

我们使用到极大似然估计法，因此需要构造关于每个已知样本  \\(\\left ( x_{i},t_{i} \\right )\\)的概率密度：

\\(P(x_{i},t_{i};w)=\\left\\{\\begin{matrix}
g(x_{i}),t_{i}=1 &\\\\
1-g(x_{i}),t_{i}=0  &
\\end{matrix}\\right.=g(x_{i})^{t_{i}}g(x_{i})^{(1-t_{i})}\\) 

可进一步表示为：

\\(P(x_{i},t_{i};w)=g(x_{i})^{t_{i}}(1-g(x_{i})^{(1-t_{i})}\\) 

有了以上的定义，我们的目标是希望通过寻找合适的\\(w\\)，使得每个样本点的似然概率最大，因此接下来就是构造似然函数，然后通过似然函数构造目标函数。

似然函数的构造的思路是假设样本独立前提下，期望每个样本的似然概率最大，换句话而言就是期望所有样本的似然概率乘积最大，即：

\\(p(D|w)=\\prod_{i=1}^{n}g(x_{i})^{t_{i}}(1-g(x_{i})^{(1-t_{i})}\\)

以上乘积通常求导数非常的困难，容易引入关联的变量，通常通过取负对数（-ln）来将乘积转化为求和，以及最大化转化为最小化形式（最优化问题通常转化为最小化问题），因此上述问题可转化为：

\\(E(w)=-\\left [ \\sum_{i=1}^{n} t_{i}ln(g(x_{i})+(1-t_{i})ln(1-g(x_{i}) \\right ]\\)

以上公式即为目标函数了。

d.优化算法

 该优化问题采用Newton-Raphson迭代优化，迭代公式为：

\\(w^{new}=w^{old}-\\mathbf{H}^{-1}\\triangledown E(w)\\)

其中\\(\\mathbf{H}\\)为\\(E(w)\\) 关于\\(w\\)的二阶导数矩阵。

\\(\\triangledown E(w)=\\sum_{i=1}^{n}(y_{i}-t_{i})x_{i}=\\mathbf{X}^{T}(\\mathbf{y}-\\mathbf{t})\\)

\\(\\mathbf{H}=\\triangledown\\triangledown E(w)=\\sum_{i=1}^{n}y_{i}(y_{i}-t_{i})x_{i}x_{i}^{T}=\\mathbf{X}^{T}\\mathbf{A}\\mathbf{X}\\) 

其中\\(\\mathbf{A}\\)为正定矩阵，即：

\\(\\mathbf{A}=\\begin{bmatrix}
g(x_1)(1-g(x_1)) & 0 & \\cdots & 0\\\\
0 & g(x_2)(1-g(x_2)) & \\cdots & 0\\\\
\\cdots & \\cdots & \\ddots & \\cdots\\\\
0 & 0 & \\cdots & g(x_n)(1-g(x_n))
\\end{bmatrix}\\)

由于\\(\\mathbf{A}\\)为正定，因此\\(\\mathbf{H}\\)也为正定矩阵。注意，\\(g(x_i)\\)的计算基于上一次的估计参数\\(w^{old}\\)来代入Logisti回归函数求解。

 

2.实现

我们举一个例子，并通过python编程求解它。问题描述为：一门考试,20位考生花费0~6小时备考。现在希望获悉备考时长与是否通过考试的关系，数据如下表格所示：

 

 

数据的解释变量仅仅为1维的学习时间,回归参数为2维向量。拟合的结果为：

\\(g(time)=\\frac{1}{1+exp(1.5046\\cdot time-4.0777)}\\)

拟合的效果图如下所示：

 

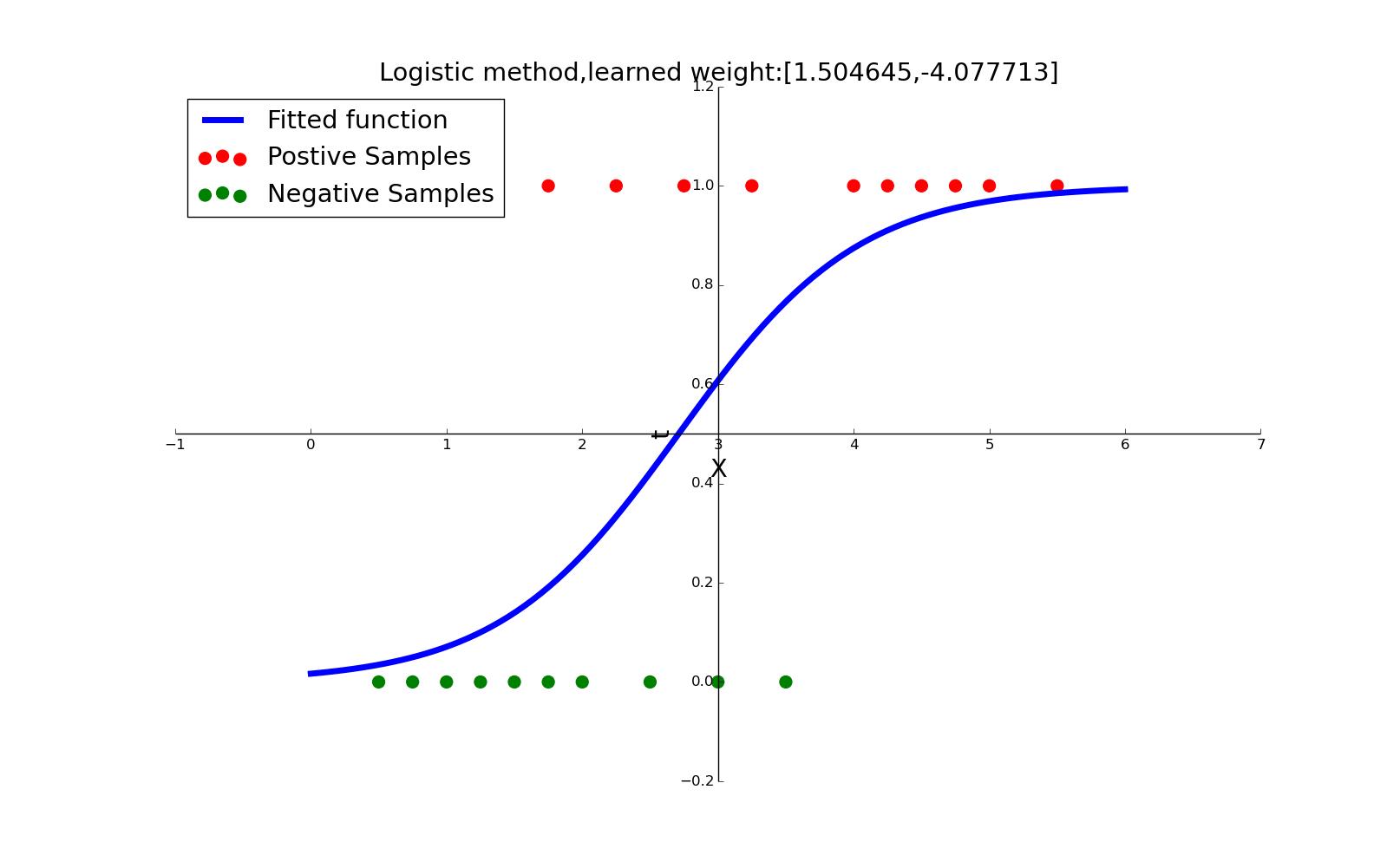
\\(w\\)迭代的梯度变化非常快，五次就能达到非常好的结果，如下所示：

[ 4.54704357]
[ 0.19111694]
[ 0.2380104]
[ 0.01743344]
[  8.45306379e-05]
[  1.95907862e-09]
[  1.90137901e-16]
[  1.90137901e-16]
[  1.90137901e-16]
[  1.90137901e-16]

 

我们使用了python实现Logistic回归，注意：我们这里对\\(\\mathbf{H}\\)是直接的求逆，如果特征维度很高的情况下，这会消耗较大的计算亮，因此我们可以采用更有效的求解方法，如Cholesky分解法，最后贴上马农最爱的代码：

import numpy as np
from matplotlib import pyplot as plt

class LogisticClassifier:
    def __init__(self):
        print("init");
        
    def logistic(self,Xa,wa):
        val = 1/(1+np.exp(-Xa.dot(wa)));
        return val;
    
    def train(self,X,t,iter_num):
        print("start to training");
        Xa = np.array(X)
        xsize = Xa.shape
        dim = xsize[1]+1
        num = xsize[0]
        Xa = np.c_[Xa,np.ones([num,1])]

        ta = np.array(t)
        
        print dim,num
        wa = 0.5*np.ones([dim,1])
        for it in range(iter_num):
            ya = self.logistic(Xa,wa)
            deriv_wa = Xa.T.dot(ya-ta)
            R = np.diag((ya*(1-ya)).flat)
            H = Xa.T.dot(R).dot(Xa)
            delta_w = np.linalg.inv(H).dot(deriv_wa)
            wa = wa - delta_w;
            print np.linalg.norm(delta_w.T, 2, 1)
            #print wa
        return wa
    
if __name__ == "__main__":
    print (\'This is main of module "hello.py"\')
    
    logCls = LogisticClassifier();
    #construct data
    X = [[0.5],[0.75],[1],[1.25],[1.5],[1.75],[1.75],[2],[2.25],[2.5],[2.75],[3],[3.25],[3.5],[4],[4.25],[4.5],[4.75],[5],[5.5]]
    t = [[0],[0],[0],[0],[0],[0],[1],[0],[1],[0],[1],[0],[1],[0],[1],[1],[1],[1],[1],[1]]
    iter_num = 10;
    #training weight
    w = logCls.train(X, t, iter_num)
    print ("learned weight:\\n")
    print w
    
    #draw and show the result       
    pos_t = [x for i, x in enumerate(t) if x == [1]]
    pos_X = [X[i] for i, x in enumerate(t) if x == [1]]
    neg_t = [x for i, x in enumerate(t) if x == [0]]
    neg_X = [X[i] for i, x in enumerate(t) if x == [0]]
    
    plt.scatter(pos_X,pos_t,color="r",marker=\'o\',s = 100)
    plt.scatter(neg_X,neg_t,color="g",marker=\'o\',s = 100)
    
    Xfitted  = np.array(np.linspace(0,6,100))
    XfittedC = np.c_[Xfitted,np.ones([100,1])]
    Yfitted = logCls.logistic(XfittedC, w)   
    plt.plot(Xfitted.flat,Yfitted.flat,color="b",linewidth= 5)
    
    #reset the axes
    ax = plt.gca()
    #no bonding box
    ax.spines[\'top\'].set_color(\'none\')
    ax.spines[\'right\'].set_color(\'none\')
    #set as zero
    ax.xaxis.set_ticks_position(\'bottom\')
    ax.spines[\'bottom\'].set_position((\'data\',0.5))
    ax.yaxis.set_ticks_position(\'left\')
    ax.spines[\'left\'].set_position((\'data\',3))

    plt.xlabel("X",fontsize="xx-large")
    plt.ylabel("t",fontsize="xx-large")
    plt.title("Logistic method,learned weight:[%f,%f]"%(w[0],w[1]),fontsize="xx-large")
    plt.legend(["Fitted function","Postive Samples","Negative Samples"],fontsize="xx-large",loc=\'upper left\');
    plt.show()
    

 

 3.参考资料

[1].Logistic回归与梯度下降法
[2].Logistic回归与牛顿迭代法