C++求一元二次方程的根
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C++求一元二次方程的根相关的知识,希望对你有一定的参考价值。
#include <iostream>
#include <cmath>
using namespace std;
void main()
int a,b,c;
float x,y;
float delta;
delta=b*b-4*a*c;
cout<<"请输入一元二次方程对应常量"<<endl;
cin>>a>>b>>c;
if(a==0&&b==0&&c!=0)
cout<<"方程无根"<<endl;
else if(a==0&&b!=0)
x=-c/b;
cout<<x<<endl;
else
if(delta=0)
x=(-b+sqrt(delta))/(2*a);
cout<<"有二个相等的实根"<<x<<endl;
else if(delta<0)
x=(-b+sqrt(delta))/(2*a);
y=(-b-sqrt(delta))/(2*a);
cout<<"方程有2个不等的复根"<<x<<y<<endl;
else
x=(-b+sqrt(delta))/(2*a);
y=(-b-sqrt(delta))/(2*a);
cout<<"方程有2个不等的根"<<x<<y<<endl;
初学 帮我看下哪儿错了 谢谢
#include <cmath>
using namespace std;
int main()
int a,b,c;
float x,y;
float delta;
cout<<"请输入一元二次方程对应常量"<<endl;
cin>>a>>b>>c;
if(a==0&&b==0&&c!=0)
cout<<"方程无根"<<endl;
else if(a==0&&b!=0)
x=-c/b;
cout<<x<<endl;
else
delta=b*b-4*a*c;
if(delta==0)
x=(-b+sqrt(delta))/(2*a);
cout<<"有二个相等的实根"<<x<<endl;
else if(delta<0)
x=(-b+sqrt(delta))/(2*a);
y=(-b-sqrt(delta))/(2*a);
cout<<"方程有2个不等的复根"<<x<<y<<endl;
else
x=(-b+sqrt(delta))/(2*a);
y=(-b-sqrt(delta))/(2*a);
cout<<"方程有2个不等的根"<<x<<y<<endl;
return 0;
你的那个if 里面 有错 你自己看看啊 还有那个delta a b c 还没有给值 怎么可以计算呢? 看看我给你的答案啊! 呵呵 高中数学学得不错啊! 情况分析的很到位! 不错! 分类分的 恰到好处! 参考技术A 这是一道经典题
我在很多地方都看到过这道题。
代码如下:
#include<stdio.h>
#include<math.h>
void
f(float
m,float
n,float
l)
float
x1,x2,q,p,deta;
deta=n*n-4*m*l;
if(deta<0)
printf("方程无解。\n");
else
q=sqrt(deta)/(2*m);
p=-n/(2*m);
x1=p+q;
x2=p-q;
if(deta==0)
printf("方程有一个解。\nx=%g\n",x1);
if(deta>0)
printf("方程有两个解。\nx1=%g,x2=%g\n",x1,x2);
main()
printf("输入a,b,c:");
float
a,b,c;
scanf("%g%g%g",&a,&b,&c);
if(a!=0)f(a,b,c);
else
if(b!=0)printf("方程是一元一次方程。\n方程的解是:X=%g。\n",-c/b);
if(b==0)printf("参数A,B,C不能够成方程。\n");
下面是程序的运行效果图: 参考技术B sqrt(delta) delta不能为负数。
C语言 求一元二次方程的根 openjudge
我的代码如下:
#include <stdio.h>
#include <math.h>
int main()
int n,j,i;
double a,b,c,r;
scanf("%d",&n);
i=0;
double arr[n][3];
while(i < n)
scanf("%lf %lf %lf",&a,&b,&c);
if(a == 0) continue;
arr[i][0] = a;
arr[i][1] = b;
arr[i][2] = c;
i++;
for(j=0;j<n;j++)
a = arr[j][0],b = arr[j][1],c = arr[j][2];
r = b*b-4*a*c;
if (r==0)
printf("x1=x2=%.5lf\n",(-b)/(2*a));
else if(r > 0)
printf("x1=%.5lf;x2=%.5lf\n",(-b+sqrt(r))/(2*a),(-b-sqrt(r))/(2*a));
else if(r < 0)
printf("x1=%.5lf+%.5lfi;x2=%.5lf-%.5lfi\n",(-b/(2*a)),(sqrt(-r)/(2*a)),(-b/(2*a)),(sqrt(-r)/(2*a)));
return 0;
疑问:代码能够得出示例的3个结果,但是通不过网上验证,题目来源是openjudge,具体见截图上网址
麻烦给指出通不过的错误在哪

—————————————————————
总时间限制: 1000ms 内存限制: 65536kB
利用公式x1 = (-b + sqrt(b*b-4*a*c))/(2*a), x2 = (-b - sqrt(b*b-4*a*c))/(2*a)求一元二次方程ax2+ bx + c =0的根,其中a不等于0。
输入
输入一行,包含三个浮点数a, b, c(它们之间以一个空格分开),分别表示方程ax2 + bx + c =0的系数。
输出
输出一行,表示方程的解。
若两个实根相等,则输出形式为:x1=x2=...。
若两个实根不等,则输出形式为:x1=...;x2 = ...,其中x1
若是两个虚根,则输出:x1=实部+虚部i; x2=实部-虚部i,其中x1,x2满足以下两个条件中的一个:
1. x1的实部大于x2的实部
2. x1的实部等于x2的实部且x1的虚部大于等于x2的虚部
所有实数部分要求精确到小数点后5位,数字、符号之间没有空格。 参考技术A 可以用结构数组,会简单点
#include <stdio.h>
#include <math.h>
struct FANC
float a;
float b;
float c;
;
int main()
void jian(double a,double b,double c);
int n;
printf("请输入待解方程的个数:\n");
scanf("%d",&n);
struct FANC str[n];
for(int i=0;i<n;i++)
printf("请输入方程的a,b,c:\n");
scanf("%lf,%lf,%lf",&str[i].a,&str[i].b,&str[i].c);
if(i>n)break;
for(int i=0;i<n;i++)
jian(str[i].a, str[i].b, str[i].c);
return 0;
void jian(double a,double b,double c)
int r;
r=b*b-4*a*c;
if(r<0)
printf("x1=%.5lf+%.5lfi;x2=%.5lf-%.5lfi\n",(-b/(2*a)),(sqrt(-r)/(2*a)),(-b/(2*a)),(sqrt(-r)/(2*a)));
else if(r==0)
printf("x1=%.5lf,x2=%.5lf\n",(-b)/(2*a),(-b)/(2*a));
else
printf("x1=%.5lf;x2=%.5lf\n",(-b+sqrt(r))/(2*a),(-b-sqrt(r))/(2*a));
里面jian函数的算法都是照搬你的,对错不知道 参考技术B scanf("%d",&n);
i=0;
double arr[n][3];
一个可能的原因就是你的编译器支持这样写未定义数组大小(忘记叫什么名字了,就是知道有这个东西,我是从来没用过,请告知一下,这个到底叫什么,我忘了)的语句,而网上不支持,就这么简单。我用VS2013编译器报错,不允许这样编写,而DEVC++却支持,主要还是要看编译器支持的标准
你可以改成。
double arr[10000000][3]; 然后用for(i=0;i<n;i++)来控制试试 参考技术C 我去是试试你的那个网址。大致问题应该是因为编译器的问题。你选择的是gcc来编译的吧。问题估计也是在这里。你的代码本身没有错。我用gcc编译也正确。但是有个问题。在引用sqrt函数是要用到math.h的头文件,gcc编译时,它有些时候是没有这个库的,需要你自己去链接。把库加入进来。我估计就是这里出问题了追问
我用的codeblocks的GCC编译器,
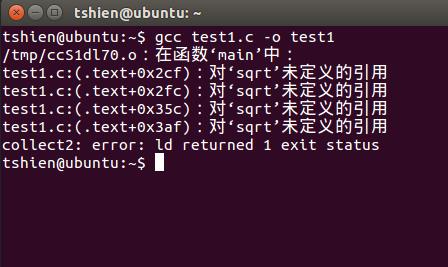
追答我知道,你看看下面的图就明白了
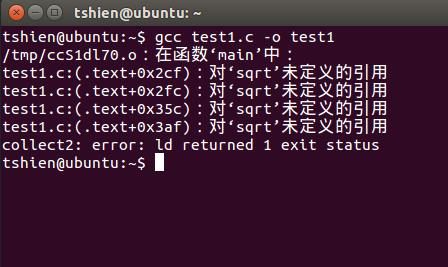
这是直接编译提示的问题,因为库里面没有math.h
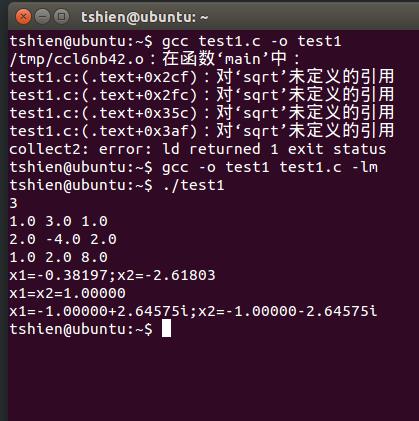
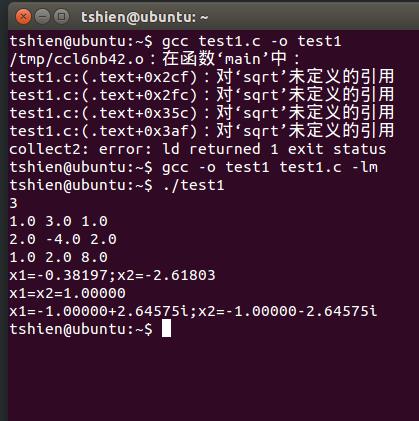
这是我自己链接math.h后才执行的。
我估计它那边也是同样的情况
以上是关于C++求一元二次方程的根的主要内容,如果未能解决你的问题,请参考以下文章