机器学习：概率校准

Posted 2020-09-24 积跬步以前行

1.再提逻辑回归

   前面已经讲过了逻辑回归，这里不再细讲，只是简单的说一个函数，主要是方便大家更好的理解概率校准。

  在逻辑回归中，用的最多的就是sigmod函数，这个函数的作用就是把无限大或者无限小的数据压缩到[0,1]之间，用来估计概率。图像大致为：

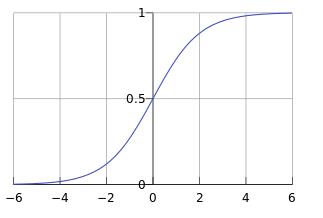
基本上是以0.5分界，0.5以上为1，0.5以下为0。但是这个分界值可以自己设定。

2.分类函数的原理

       在进行分类时，基本上和逻辑回归的原理一样，计算出某个数据属于各分类的概率，然后取概率最大的那个作为最终的分类标签。

       但是假设我们考虑这样的一种情况：在二分类中，属于类别0的概率为0.500001，属于类别1的概率为0.499999。假若按照0.5作为判别标准，那么毋庸置疑应该划分到类别0里面，但是这个真正的分类却应该是1。如果我们不再做其他处理，那么这个就属于错误分类，降低了算法的准确性。

       如果在不改变整体算法的情况下，我们是否能够做一些补救呢？或者说验证下当前算法已经是最优的了呢？

       这个时候就用到了概率校准。

3.Brier分数

       在说概率校准前，先说下Brier分数，因为它是衡量概率校准的一个参数。

       简单来说，Brier分数可以被认为是对一组概率预测的“校准”的量度，或者称为“ 成本函数 ”，这一组概率对应的情况必须互斥，并且概率之和必须为1.

       Brier分数对于一组预测值越低，预测校准越好。

       其求解公式如下：(此公式只适合二分类情况，还有原始定义公式)

       

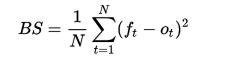
     其中 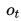 是预测的概率，是事件t的实际概率（如果不发生则为0），而N是预测事件数量。

     引用维基百科的一个例子说明 Brier分数的计算方式：   

     假设一个人预测在某一天会下雨的概率P，则Brier分数计算如下：
          如果预测为100％（P = 1），并且下雨，则Brier Score为0，可达到最佳分数。
          如果预测为100％（P = 1），但是不下雨，则Brier Score为1，可达到最差分数。
          如果预测为70％（P = 0.70），并且下雨，则Brier评分为（0.70-1）² = 0.09。
          如果预测为30％（P = 0.30），并且下雨，则Brier评分为（0.30-1）² = 0.49。
          如果预测为50％（P = 0.50），则Brier分数为（0.50-1）² =（0.50-0）² = 0.25，无论是否下雨。

4.概率校准

          概率校准就是对分类函数做出的分类预测概率重新进行计算，并且计算Brier分数，然后依据Brier分数的大小判断对初始预测结果是支持还是反对。

5.举例说明

  1）核心函数

        a）sklearn.calibration.CalibratedClassifierCV

        b）主要参数：

             base_estimator ：初始分类函数

             method ：校准采用的方法。取值‘sigmoid’ 或者 ‘isotonic’

             cv ：交叉验证的折叠次数。

         c）详细代码及说明            

from sklearn.naive_bayes import GaussianNB
import numpy as np
from sklearn.calibration import CalibratedClassifierCV
from sklearn.metrics import brier_score_loss

x_train = np.array([[1,2,3],[1,3,4],[2,1,2],[4,5,6],[3,5,3],[1,7,2]])
y_train = np.array([0, 0, 0, 1, 1, 1])
x_test = np.array([[2,2,2],[3,2,6],[1,7,4],[2,5,1]])#
y_test = np.array([0, 1, 1, 1]) #

clf = GaussianNB()
clf.fit(x_train, y_train)

##返回预测标签
y_pred = clf.predict(x_test)
print("******预测的分类值***************************")
print(y_pred)

##返回预测属于某标签的概率
prob_pos_clf = clf.predict_proba(x_test)
print("******属于某个类的概率*************************")
print(prob_pos_clf)
print("******Brier scores*************************")
clf_score = brier_score_loss(y_test, y_pred)
print(clf_score)


##进行概论校准
clf_isotonic = CalibratedClassifierCV(clf, cv=2, method=\'isotonic\')
clf_isotonic.fit(x_train, y_train)

##校准后的预测值
print("******第一次概率校准后的预测分类*************************")
y_pred1 = clf_isotonic.predict(x_test)
print(y_pred1)

##校准后属于某个分类的概率
print("******第一次概率校准后属于某个类的概率******************")
prob_pos_isotonic = clf_isotonic.predict_proba(x_test)
print(prob_pos_isotonic)

print("******Brier scores*************************")
clf_isotonic_score = brier_score_loss(y_test, y_pred1, pos_label = 0)
print(clf_isotonic_score)

##进行概论校准
clf_sigmoid = CalibratedClassifierCV(clf, cv=2, method=\'sigmoid\')
clf_sigmoid.fit(x_train, y_train)

##校准后的预测值
print("*******第二次概率校准后的预测分类*************************")
y_pred2 = clf_sigmoid.predict(x_test)
print(y_pred2)

##校准后属于某个分类的概率
print("*******第二次概率校准后属于某个类的概率**************************")
prob_pos_sigmoid = clf_sigmoid.predict_proba(x_test)
print(prob_pos_sigmoid)
print("******Brier scores*************************")
clf_sigmoid_score = brier_score_loss(y_test, y_pred2, pos_label = 1)
print(clf_sigmoid_score)

View Code

         d）代码输出及说明

        举这个例子只是为了说明概率校准，所以有些地方可能不是很严谨。

******预测的分类值***************************
[0 1 1 1]
******属于某个类的概率*************************
[[  9.99748066e-01   2.51934113e-04]
 [  6.85286666e-02   9.31471333e-01]
 [  1.13899717e-07   9.99999886e-01]
 [  6.91186866e-04   9.99308813e-01]]
******Brier scores*************************
0.0
******第一次概率校准后的预测分类*************************
[0 0 1 1]
******第一次概率校准后属于某个类的概率******************
[[ 0.75  0.25]
 [ 0.75  0.25]
 [ 0.25  0.75]
 [ 0.25  0.75]]
******Brier scores*************************
0.75
*******第二次概率校准后的预测分类*************************
[0 0 1 1]
*******第二次概率校准后属于某个类的概率**************************
[[ 0.62500028  0.37499972]
 [ 0.62500028  0.37499972]
 [ 0.37500027  0.62499973]
 [ 0.37500027  0.62499973]]
******Brier scores*************************
0.25

     首先，说下概率校准，通过上面的输出可以看出，对于第二个数[3,2,6]，第一次预测结果的概率为[  6.85286666e-02   9.31471333e-01]，第一次校准后的概率变成了[ 0.75  0.25]，因为0.75>0.25，所以又被划分到了类别0，第二次校准后的概率变成了[ 0.62500028  0.37499972]，所以也被划分到了类别0.虽然校准后的分类错了，但是也可以很好说明概率校准的作用。

     其次，说下Brier scores，三次依次为0.0，0.75，0.25，根据越小越好的原则，初始分类函数已经是最优解了。

     第三，说下Brier scores中的0.75跟0.25，在代码中会发现brier_score_loss(y_test, y_pred2, pos_label = 1)中参数pos_label的值是不一样的，一个是0，一个是1，当pos_label取值为1或者默认时，Brier scores中的0.75也会变成0.25，官方对pos_label的解释为：Label of the positive class. If None, the maximum label is used as positive class，怎么翻译都不好理解，所以这里就不翻译了。但是经过我的多次实验发现，在二分类中，pos_label取值为1或者默认时，表示的应该是分类错误的百分比，pos_label=0则表示分类正确的百分比。