HDU 5434 Peace small elephant 状压dp+矩阵快速幂

Posted 2020-06-23

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=5434

Peace small elephant

 

 Accepts: 38

 

 Submissions: 108

 Time Limit: 10000/5000 MS (Java/Others)

 

 Memory Limit: 65536/65536 K (Java/Others)

问题描述

小明很喜欢国际象棋，尤其喜欢国际象棋里面的大象(只要无阻挡能够斜着走任意格)，但是他觉得国际象棋里的大象太凶残了，于是他想到了小象，
小象就没有大象那么凶残，它的攻击范围是它当前格子直角所斜对的格子。现在小明要在棋盘上放很多个小象，有趣的是，当两个小象所在格子有公共边时，
它们将合体变成合体象，多个小象满足条件也会合体，合体象的攻击范围也是它所覆盖格子区域直角所斜对的格子，现在要求任何一个象的攻击范围上是空的(即不摆放棋子)，
小明的棋盘很特殊，有m*nm∗n个格子，求满足条件的摆放的方案数，由于方案数太大，需要对10000000071000000007取模。
下面给出几种形状下的象的攻击范围图，叉号表示攻击范围。

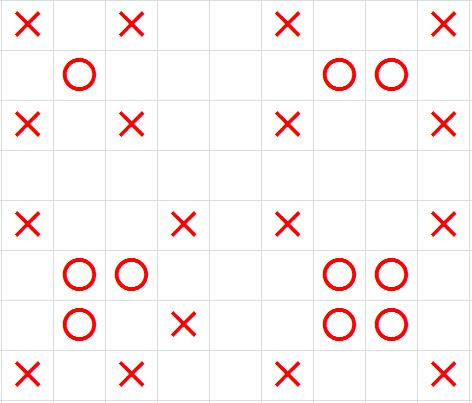
输入描述

输入有多组数据(最多55组)，每组数据有两个整数n,mn,m含义如题目描述。
1 \leq m \leq 7,1 \leq n \leq 10000000001≤m≤7,1≤n≤1000000000

输出描述

每组数据对应输出一行包含一个整数,表示满足条件的摆放的方案数。

输入样例

1 1
2 3

输出样例

2
50

题解：

　　状压dp+矩阵快速幂。

　　做了好几天，终于敲出来了！。。

　　详细题解，明天补充，先睡为敬>

代码：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 using namespace std;
 5 
 6 const int maxn = 155;
 7 const int mod = 1000000007;
 8 
 9 typedef long long LL;
10 
11 struct Matrix {
12     int n, m;
13     int val[maxn][maxn];
14     Matrix(int n,int m) :n(n),m(m) {}
15     Matrix() {}
16     void init(int n, int m) { this->n = n; this->m = m; }
17     friend Matrix operator * (const Matrix& mat1, const Matrix& mat2) {
18         Matrix ret(mat1.n, mat2.m);
19         for (int i = 0; i < ret.n; i++) {
20             for (int j = 0; j < ret.m; j++) {
21                 ret.val[i][j] = 0;
22                 for (int k = 0; k < mat1.m; k++) {
23                     ret.val[i][j] += (LL)mat1.val[i][k] * mat2.val[k][j]%mod;
24                     ret.val[i][j] %= mod;
25                 }
26             }
27         }
28         return ret;
29     }
30 };
31 
32 void power(Matrix& mat, int n, Matrix& ans) {
33     while (n > 0) {
34         if (n % 2) ans = mat*ans;
35         mat = mat*mat;
36         n /= 2;
37     }
38 }
39 
40 int _n, m;
41 
42 bool isOk(int s1, int s2) {
43     for (int i = 0; i<m; i++) {
44         if ((s1&(1 << i)) && !(s2&(1 << i))) {
45             int j;
46             j = i - 1;
47             if (j >= 0) {
48                 if ((s2&(1 << j)) && !(s1&(1 << j))) return false;
49             }
50             j = i + 1;
51             if (j<m) {
52                 if ((s2&(1 << j)) && !(s1&(1 << j))) return false;
53             }
54         }
55     }
56     return true;
57 }
58 
59 Matrix mat, ans;
60 
61 void init() {
62     mat.init(1 << m, 1 << m);
63     for (int i = 0; i<mat.n; i++) {
64         for (int j = 0; j<mat.m; j++) {
65             if (isOk(i, j)) mat.val[i][j] = 1;
66             else mat.val[i][j] = 0;
67         }
68     }
69 
70     ans.init(1 << m, 1);
71     for (int i = 0; i < ans.n; i++) ans.val[i][0] = 1;
72 }
73 
74 int main() {
75     while (scanf("%d%d", &_n, &m) == 2 && _n) {
76         init();
77         power(mat, _n - 1, ans);
78         int res = 0;
79         for (int i = 0; i < ans.n; i++) {
80             res += ans.val[i][0];
81             res %= mod;
82         }
83         printf("%d\n", res);
84     }
85     return 0;
86 }

View Code