独立性检验原理
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了独立性检验原理相关的知识，希望对你有一定的参考价值。
参考技术A独立性检验是统计学的一种检验方式。与适合性检验同属于X2检验（即卡方检验，英文名：chi square test）它是根据次数资料判断两类因子彼此相关或相互独立的假设检验，原理是为了检验两个变量是否独立！
在做项目的时候，我们有几百万的样本，如果用全部的样本去做卡方检验的话，会出现这种情况：
除了随机属性，90%以上的属性与标签（二分类）的卡方检验都是显著的。这样的话对于属性和标签的卡方检验还有什么意义？
其实这里涉及到卡方检验的灵敏度问题，样本量越大卡方检验越灵敏。
在r不变的情况下样本量越大导致e越大，导致卡方统计量x越大，导致p值越小。
所以就得出了我们的结论：样本量越大，卡方检验越灵敏。
回到我们的例子，如果用几百万的数据去做卡方检验的话，卡方检验就十分灵敏，两个变量稍微的相关都能检查出来，但这样检查出来的变量是我们想要的吗？
显然不是，因为加入变量是有成本的：
1、计算成本
2、过拟合风险
3、由于共线性导致的变量失效
所以不是所有相关的变量我们都要列入模型中，而是对模型贡献大的变量要列入模型中。
所以我们要的是容易检查出相关性的变量。要实现这个目的就要让卡方检验不那么灵敏，即减少卡方检验的样本量。
2021 年 五一数学建模比赛 C 题
文章目录
本人专挑数据挖掘、机器学习和 NLP 类型的题目做，有兴趣也可以逛逛我的数据挖掘竞赛专栏。
如果本篇博文对您有所帮助，请不要吝啬您的点赞 😊
赛题官网：http://51mcm.cumt.edu.cn/
思路
这道题的突破口就在于如何解决第一问，若能够在第一问便提出一种量化评价风险的方法，下面的题就好解决了。
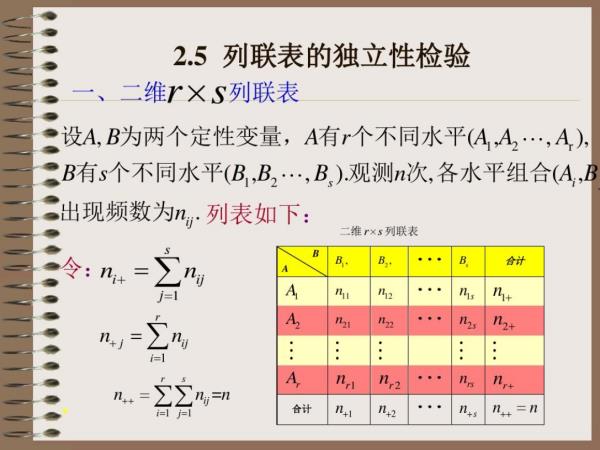
如何量化呢？这里用统计的方法，对每一个感知器的所有时序数据（共 5519 个），从冲击性风险、独立性和偶发性风险、以及自相关风险三个方面，来评价感知器的风险值。
至于第二问，我们可以沿用第二问的方法，以 30 分钟为间隔，算出每个感应器的异常得分（得分用第一问方法求出），求这段时间内感应器异常得分的总和，找出前 5 个异常得分总和最大的时刻即可。并把异常总得分，作为该时刻的异常得分。之后，在每个最异常的时刻上，找出 5 个异常得分最大的感应器。
至于第三问，我们根据移动平均算法，求出未来 15 分钟的风险值即可。
至于第四问，都算出风险了，安全评分还会远吗？
第一问
从题目可知，数据存在波动，波动分成两种：
- 正常波动：外界温度或者产量变化的波动，传感器误报，规律性、独立性、偶发性
- 非正常波动：生产过程中的不稳定因素，持续性、联动性
注意，正常波动中，有一个规律性，所以，正常波动是白噪声吗？
我们把没有持续性和联动性的参数，就叫非正常波动。
风险分析
我们来看看题目对风险的定义：
这些异常性波动的出现是生产过程中的不稳定因素造成的，预示着可能存在安全隐患，我们视为风险性异常
所以，感应器误识别，和因温度等因素引起的独立性和偶发性波动，都不是风险。
独立性、偶发性误差（非风险也）
这种独立性、偶发性的误差，将原本相对平稳的变量，添加上了白噪声，造成数据带有这种白噪声误差的原因可能是感应器误识别，温度、振动等外部环境：
风险
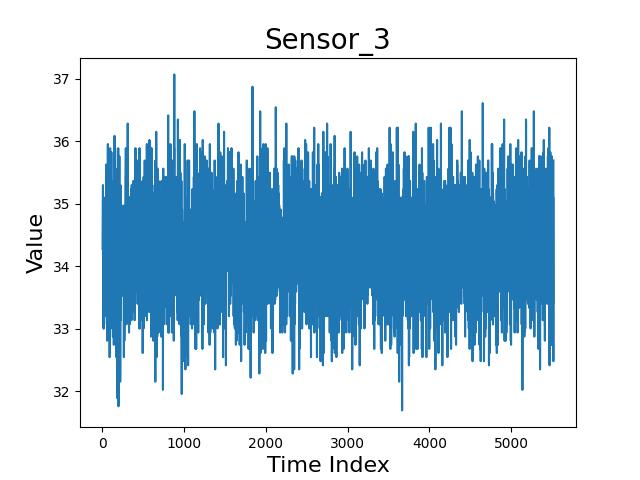
根据题目，所谓风险应该是有持续性的、联动性的，如下所示：
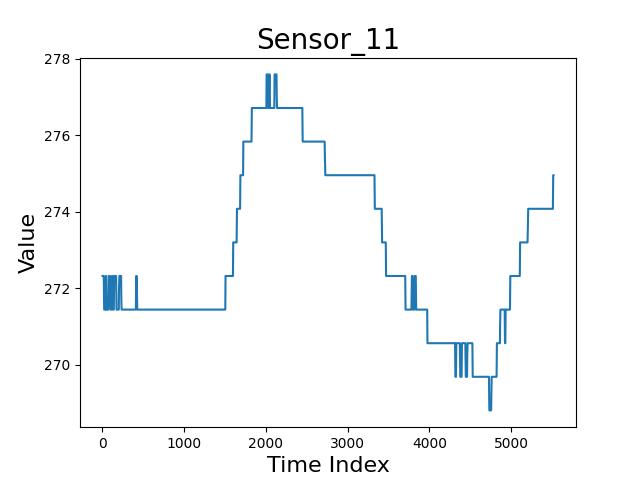
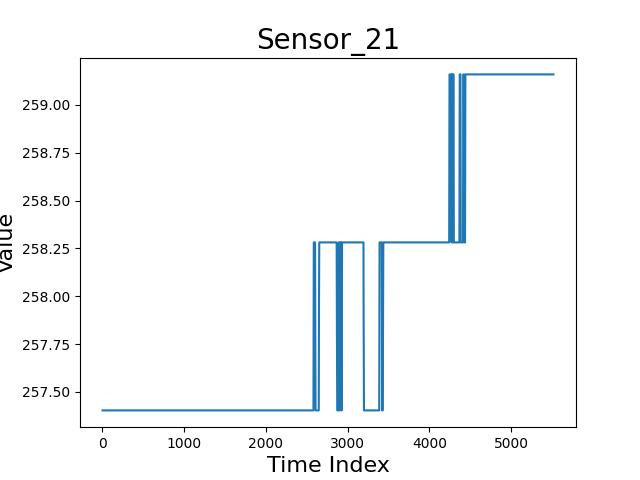
灰色地带
规律性波动
有一些传感器变量，它的变量波动很大，如下所示：
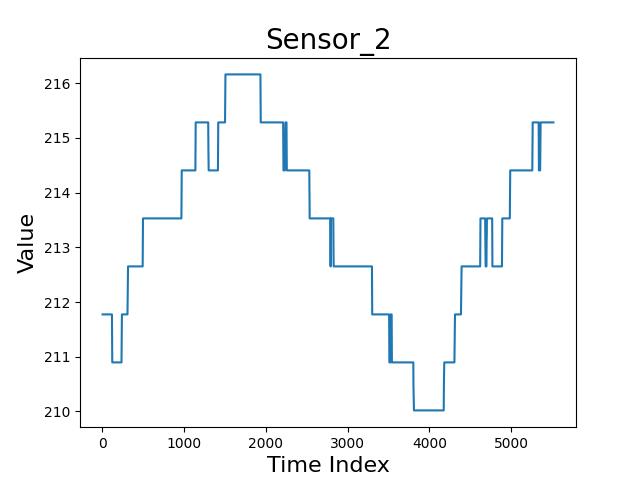
从题目可知，有些误差是具有规律性的，但规律性，又意味着联动性和持续性。所以，对传感器 2 来说，我们可以说是因为温度等因素，也可以归咎于生产过程。
但对本题而言，我们将类似传感器 2 的规律性波动，视为风险。
冲击性误差
如下所示，个人理解认为，感应器 10 和 感应器 5 中的冲击性波动，不应该理解为感应器的误差，而应该视为生产过程中的冲击性干扰。
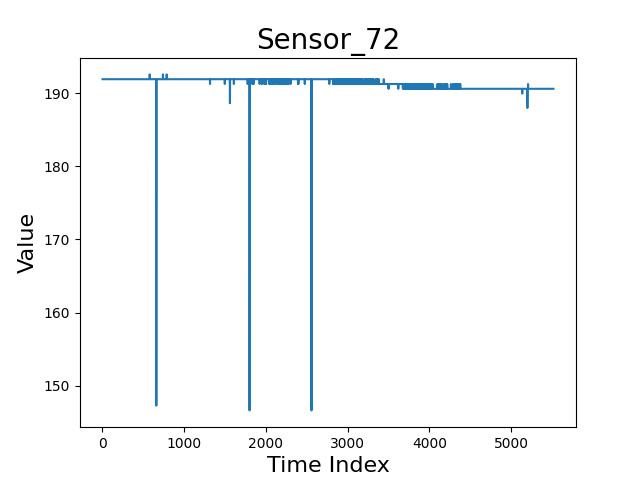
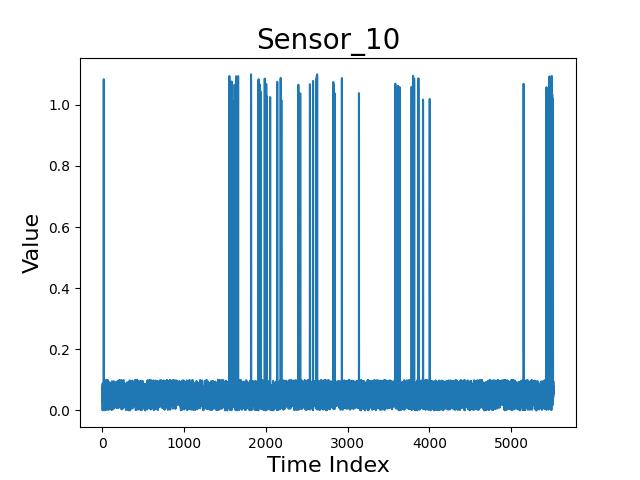
冲击性风险判定与算法 A
算法 A 来自 GB/T 6379.5，应用此算法计算得到数据平均值和标准差的稳健值，但也可以据此统计冲击性风险的数据含量。
算法 A 的计算过程如下所示：
首先是计算初始值：
x
∗
=
med
x
i
s
∗
=
1.483
×
med
∣
x
i
−
x
∗
∣
\\begin{array}{c} x^{*}=\\operatorname{med} x_{i} \\\\ s^{*}=1.483 \\times \\operatorname{med}\\left|x_{i}-x^{*}\\right| \\end{array}
x∗=medxis∗=1.483×med∣xi−x∗∣
对每个
x
i
x_i
xi，有：
x
i
∗
=
{
x
∗
−
δ
,
若
x
i
<
x
∗
−
δ
x
∗
+
δ
,
若
x
i
>
x
∗
+
δ
x
i
,
其他
x_{i}^{*}=\\left\\{\\begin{array}{cc} x^{*}-\\delta, & \\text { 若 } x_{i}<x^{*}-\\delta \\\\ x^{*}+\\delta, & \\text { 若 } x_{i}>x^{*}+\\delta \\\\ x_{i}, & \\text { 其他 } \\end{array}\\right.
xi∗=⎩⎨⎧x∗−δ,x∗+δ,xi, 若 xi<x∗−δ 若 xi>x∗+δ 其他
其中：
δ
=
1.5
s
∗
\\delta=1.5 s^{*}
δ=1.5s∗，再次计算：
x
∗
=
∑
x
i
∗
/
p
s
∗
=
1.134
∑
(
x
i
∗
−
x
∗
)
2
/
(
p
−
1
)
\\begin{array}{c} x^{*}=\\sum x_{\\mathrm{i}}^{*} / p \\\\ s^{*}=1.134 \\sqrt{\\sum\\left(x_{\\mathrm{i}}^{*}-x^{*}\\right)^{2} /(p-1)} \\end{array}
x∗=∑xi∗/ps∗=1.134∑(xi∗−x∗)2/(p−1)
重复：
x
i
∗
=
{
x
∗
−
δ
,
若
x
i
<
x
∗
−
δ
x
∗
+
δ
,
若
x
i
>
x
∗
+
δ
x
i
,
其他
x_{i}^{*}=\\left\\{\\begin{array}{cc} x^{*}-\\delta, & \\text { 若 } x_{i}<x^{*}-\\delta \\\\ x^{*}+\\delta, & \\text { 若 } x_{i}>x^{*}+\\delta \\\\ x_{i}, & \\text { 其他 } \\end{array}\\right.
xi∗=⎩⎨⎧x∗−δ,x∗+δ,xi, 若 xi<x∗−δ 若 xi>x∗+δ 其他
直到 s ∗ s^* s∗ 的 第三位有效数字和 x ∗ x^* x∗ 的对应数字在连续两次迭代中不变。
因此，对感应器的数据，我们通过算法 A 后，得到最终的 x i ∗ x_i^* xi∗，记取值为 x ∗ + δ x^*+\\delta x∗+δ 或 x ∗ − δ x^*-\\delta x∗−δ 的 x i ∗ x_i^* xi∗ 的数量为 m m m，于是冲击性风险为 m / n m/n m/n 。
我们也可以搞复杂一点，因为冲击性持续时间越长，意味着风险越大。因此，若取值为 x ∗ + δ x^*+\\delta x∗+δ 或 x ∗ − δ x^*-\\delta x∗−δ的数连续出现，我们可以给其添加权重。
如出现以及，记为 1 分，连续出现 2 次，记为 1 + 2 1+2 1+2，连续出现 3 次，记为 1 + 2 + 3 1+2+3 1+2+3 …，若间隔出现 2 次，则记为 1 + 1 1 + 1 1+1，以此类推，最终求和得到 m ′ m^\\prime m′。
于是，冲击性风险即为：
r
i
s
k
1
=
m
′
n
risk_1 =\\frac {m^\\prime}{n}
risk1=nm′以上是关于独立性检验原理的主要内容，如果未能解决你的问题，请参考以下文章
R语言分类变量独立性检验（Tests of independence）使用Fisher精确检验fisher.test函数检验分类变量的独立性（ test of independence）