递归与分治-合并排序快速排序以及循环赛问题

Posted 2020-09-23 晓乎

　合并排序

　　合并排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

　　递归方法：

　　　　基本思想是：将待排序元素分成大小一致相同的2个子集和，分别对两个子集和进行排序，最终将排好序的子集合并成所需要的排好序的集合

package com.gqx.arithmetic.Recursion;

public class Recursion_Merge2 {

	private static void mergeSort(int a[],int left,int right) {
		int[] b=new int[a.length];
		if (left<right) {
			int i=(left+right)/2;
			mergeSort(a, left, i);
			mergeSort(a, i+1, right);
			merge(a,b,left,i,right);	//合并数组到b中
			copy(a, b, left, right);	//复制回数组a中
		}

	}

	private static void copy(int[] a, int[] b, int left, int right) {
		// TODO Auto-generated method stub
		for (int i = left; i <= right; i++) {
			a[i]=b[i];
		}
	}

	private static void merge(int[] x, int[] y, int i, int j, int k) {
		// TODO Auto-generated method stub
		//合并c[i:j]和c[j+1:k]
		int t=i,h=i,u=j+1;
		while ( (t <= j) && (u<=k) ) {
			if (x[t]<=x[u]) {
				y[h++]=x[t++];
			}else {
				y[h++]=x[u++];
			}
		}

		//若果两个c[i:j]和c[j+1:k]还有元素没有被比较，
		if (t>j) 
			//t>j 说明前面i个数已经加到了y中，而后面的(j-k)还未全部加到y中
			for (int l = u; l <= k; l++) {
				y[h++]=x[l];
			}
		else {
			//如果后面的(j-k)已经加到了y中，而前面的(i-j)还未加到y中
			for(int l=t;l<=j;l++)
				y[h++]=x[l];
		}
	}

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int a[]={55,11,44,88,67,22,88,33};
		mergeSort(a, 0, a.length-1);
		System.out.println("递归方式实现归并排序：");
		for (int i = 0; i < a.length; i++) 
			System.out.print(a[i]+"\\t");
	}

}

　递归中只是将待排序的集合一分为二，直至待排序的集合只剩下一个元素为止，然后不断地合并两个已经排好序的数组段。结果如图：

　　分治方法：

　　消除递归，按照自然排序的基本思想。

package com.gqx.arithmetic.Recursion;

public class Recursion_Merge {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] a={2,45,66,8,22,67,90,33,1};
		for (int i = 0; i < a.length; i++)
			System.out.print(a[i]+"\\t");
		System.out.println();
		System.out.println("分治方法排序结果如下：");
		int[] s=mergeSort(a);
		for (int i = 0; i < s.length; i++)
			System.out.print(s[i]+"\\t");
	}

	//使用非递归方法
	public static int[] mergeSort(int a[])
	{
		int b[]=new int[a.length];
		int s=1;
		/*
		 * 将数组a分为a.length个独立的数组（每个元素都是一个数组），
		 * 然后（1,2），（3,4）....（a.length-1,a.length)进行排序，即可得到a.lenthg/2个数组（已经排好序）放到b中
		 * 然后在对b进行排序（以每两个元素为一组，然后继续进行排序，此时数组的分组继续减半，重新放到a中去，最后要返回a数组
		 */
		while (s<a.length) {
			mergePass(a,b,s);
			s+=s;
			mergePass(b, a, s);
			s+=s;
		}
		return a;
	}

	private static void mergePass(int[] a, int[] b, int s) {
		// TODO Auto-generated method stub
		//合并大小为s的相邻子数组
		int i=0;
		while(i<=a.length-2*s){
			//合并大小为s的相邻的两个段子数组
			merge(a, b, i, i+s-1, i+s*2-1);
			i=i+2*s;
		}
		//剩余元素少于两个
		if (i+s<a.length) {
			//若最后只剩下n-1个元素和1个元素进行合并排序
			merge(a, b, i, i+s-1, a.length-1);
		}
		else {
			//因为在前面的while中都是以2的幂次方进行分组的，若a为奇数，则剩余部分需要加上
			//复制到y
			for (int j = i; j < a.length; j++) {
				b[j]=a[j];
			}
		}
	}

	private static void merge(int[] x, int[] y, int i, int j, int k) {
		// TODO Auto-generated method stub
		//合并c[i:j]和c[j+1:k]
		int t=i,h=i,u=j+1;
		while ( (t <= j) && (u<=k) ) {
			if (x[t]<=x[u]) {
				y[h++]=x[t++];
			}else {
				y[h++]=x[u++];
			}
		}

		//若果两个c[i:j]和c[j+1:k]还有元素没有被比较，
		if (t>j) 
			//t>j 说明前面i个数已经加到了y中，而后面的(j-k)还未全部加到y中
			for (int l = u; l <= k; l++) {
				y[h++]=x[l];
			}
		else {
			//如果后面的(j-k)已经加到了y中，而前面的(i-j)还未加到y中
			for(int l=t;l<=j;l++)
				y[h++]=x[l];
		}

	}


}

　　结果如图：

---

 

快速排序：

　　其基本思想是：在一趟排序中将要排序的数据分割成独立的两部分，其中一部分序列的关键字（这里主要用值来表示）均比另一部分关键字小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。算法如下。

package com.gqx.arithmetic.Recursion;

public class QuickSort {
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int a[]={2,45,66,8,22,67,90,33,1};
		new QuickSort().qSort(a, 0, a.length-1);
		for (int i = 0; i < a.length; i++) {
			System.out.print(a[i]+"\\t");
		}
	}
	
	private void qSort(int a[],int p,int r) {
		if (p<r) {
			int q=partition(a,p,r);
			qSort(a, p, q-1);
			qSort(a, q+1, r);
		}
	}

	//对a[p:r]进行划分，以元素x=a[p]作为划分的基准，分别从左右两端开始，扩展两个区域a[p:i]和a[j:r];
	//使得a[p:i]中元素小于或等于x;而a[j:r]中元素大于等于x
	//初始时，i=p,且j=r+1
	private int partition(int a[], int p, int r) {
		// TODO Auto-generated method stub
		int i=p,j=r+1;
		int x=a[p];
		//将<x的元素交换到左边区域
		//将>x的元素交换到右边区域
		while (true) {
			while (a[++i]<x && i<r);
			while(a[--j]>x);
			if (i>=j)
				break;
			swap(a,i,j);
		}
		a[p]=a[j];
		a[j]=x;
		return j;
	}

	private void swap(int[] a, int i, int j) {
		// TODO Auto-generated method stub
		int temp=a[j];
		a[j]=a[i];
		a[i]=temp;
	}

}

　　输出如图：

 

---

 

循环赛问题：

问题描述：       

   设有n=2k个选手要进行网球循环赛，要求设计一个满足以下要求的比赛日程表：

（1）每个选手必须与其他n-1个选手各赛一次；
（2）每个选手一天只能赛一次。

       按此要求，可将比赛日程表设计成一个 n 行n-1列的二维表，其中，第 i 行第 j 列表示和第 i 个选手在第 j 天比赛的选手。

 问题分析：

　　实际上就是将问题的在一个方阵的二位数组中实现值得关于中心点赋值的过程，如图所示，当只有两个选手的时候：

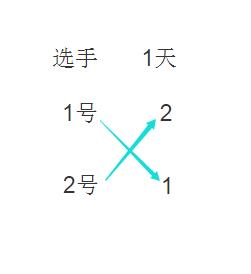
当有四个选手的时候：

 

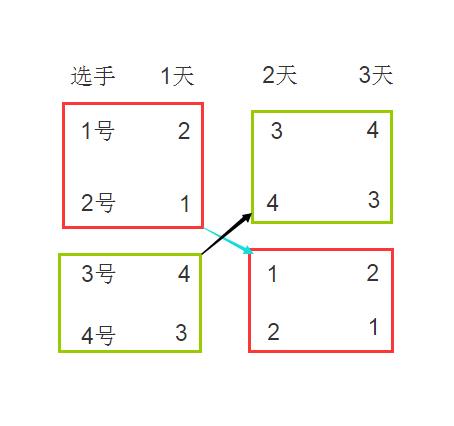
 同理：当有八个选手的时候，如图：

 

 就由此得到规律。其算法程序如下：

package com.gqx.arithmetic.Recursion;

public class LoopRace {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int x[][]=table(3);
		for (int i = 1; i < x.length; i++) {
			for (int j = 1; j < x[i].length; j++) {
				System.out.print(x[i][j]+"\\t");
			}
			System.out.println();
		}
	}

	public static int[][] table(int k){
		int n=1;
		for (int i = 1; i <= k ; i++) 
			n*=2;		//初始化选手人数
		int  a[][]=new int[n+1][n+1];
		for (int i = 1; i <= n; i++) 
			a[1][i]=i;	//初始化第一行，然后进行复制
		int m=1;
		for(int s=1;s<=k;s++){
			n/=2;
			for (int t = 1; t <= n; t++) 
				for(int i=m+1;i<=2*m;i++)
					for(int j=m+1;j<=2*m;j++){
						a[i][j+(t-1)*m*2]=a[i-m][j+(t-1)*m*2-m];
						a[i][j+(t-1)*m*2-m]=a[i-m][j+(t-1)*m*2];
					}
			m*=2;
		}
		
		return a;
	}

}

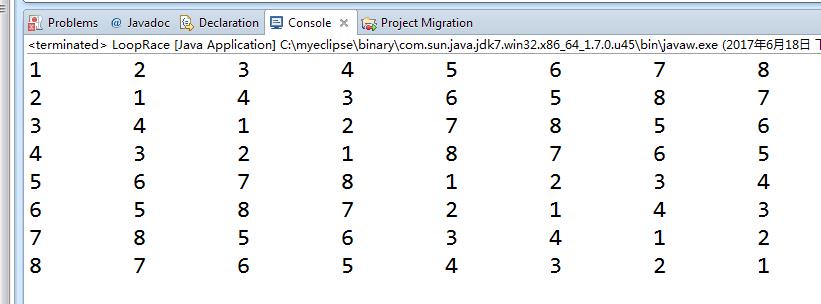
 输出如图：