浅析线性表的原理及简单实现

Posted 2020-09-23

一、线性表

原理：零个或多个同类数据元素的有限序列

原理图：

特点 ： 

1、有序性

2、有限性

3、同类型元素

4、第一个元素无前驱，最后一个元素无后继，中间的元素有一个前驱并且有一个后继

线性表是一种逻辑上的数据结构，在物理上一般有两种实现 顺序实现和链表实现 

 

二、基于数组的 线性表顺序实现

原理 ： 用一段地址连续的存储单元依次存储线性表数据元素。

原理图：

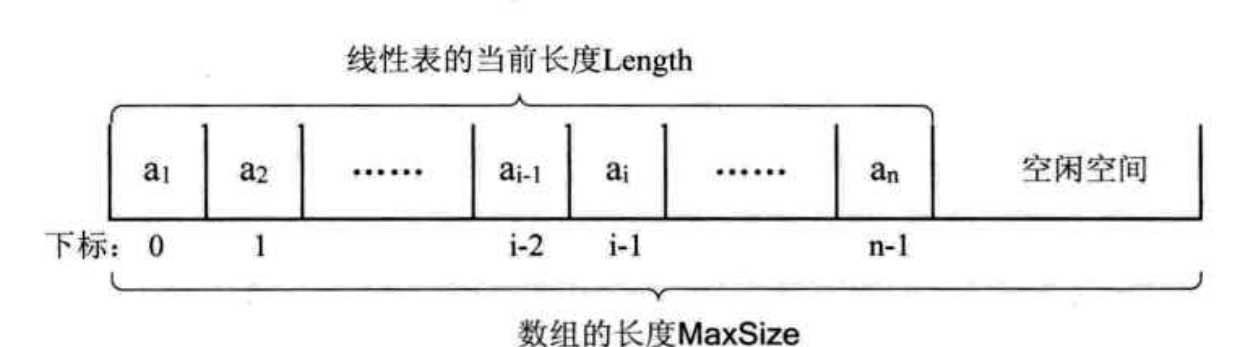
算法原理：

1、初始化一个定长的数组空间 elementData[] , size 存储长度 存储元素

2、通过索引来快速存取元素

3、通过数组复制实现元素的插入和删除

实现代码：

接口定义：

 1 package online.jfree.base;
 2 
 3 /**
 4  * author : Guo LiXiao
 5  * date : 2017-6-14  11:46
 6  */
 7 
 8 public interface LineList <E>{
 9 
10     /**
11      * lineList 是否为空
12      * @return
13      */
14     boolean isEmpty();
15 
16     /**
17      * 清空 lineList
18      */
19     void clear();
20 
21     /**
22      * 获取指定位置元素
23      * @param index
24      * @return
25      */
26     E get(int index);
27 
28     /**
29      * 获取元素第一次出现的位置
30      * @param e
31      * @return
32      */
33     int indexOf(E e);
34 
35     /**
36      * 判断 lineList是否包含指定元素
37      * @param e
38      * @return
39      */
40     boolean contains(E e);
41 
42     /**
43      * 设置指定位置数据，如数据已存在 则覆盖原数据
44      * @param index
45      * @param e
46      * @return
47      */
48     E set(int index, E e);
49 
50     /**
51      * 移除指定位置元素
52      * @param index
53      * @return
54      */
55     E remove(int index);
56 
57     /**
58      * 在lineList结尾插入元素
59      * @param e
60      * @return
61      */
62     E add(E e);
63 
64     /**
65      * 在index后面插入元素
66      * @param index
67      * @param e
68      * @return
69      */
70     E add(int index, E e);
71 
72     /**
73      * 返回lineList长度
74      * @return
75      */
76     int size();
77 
78 
79 
80 }

View Code

算法实现：

  1 package online.jfree.base;
  2 
  3 /**
  4  * author : Guo LiXiao
  5  * date : 2017-6-15  13:44
  6  */
  7 
  8 public class OrderedLineList<E> implements LineList<E> {
  9 
 10     private static final int INIT_CAPACITY = 10;
 11 
 12     private transient E[] elementData;
 13 
 14     private transient int elementLength;
 15 
 16     private int size;
 17 
 18     public OrderedLineList() {
 19         this(0);
 20     }
 21 
 22     public OrderedLineList(int initCapacity) {
 23         init(initCapacity);
 24     }
 25 
 26     private void init(int initCapacity) {
 27         if (initCapacity >= 0) {
 28             this.elementData = (E[]) new Object[initCapacity];
 29             this.elementLength = initCapacity;
 30         } else {
 31             throw new IllegalArgumentException("Illegal Capacity: " +
 32                     initCapacity);
 33         }
 34         this.size = 0;
 35     }
 36 
 37     /**
 38      * 扩容
 39      */
 40     private void dilatation() {
 41         int oldCapacity = this.elementLength;
 42         int newCapacity = oldCapacity;
 43         if (oldCapacity <= this.size) {
 44             newCapacity = oldCapacity + INIT_CAPACITY;
 45         }else if(oldCapacity - INIT_CAPACITY > this.size){
 46             newCapacity = oldCapacity - INIT_CAPACITY;
 47         }
 48         if (oldCapacity != newCapacity){
 49             E[] newElementData = (E[]) new Object[newCapacity];
 50             System.arraycopy(elementData, 0, newElementData, 0, oldCapacity);
 51             this.elementLength = newCapacity;
 52             this.elementData = newElementData;
 53         }
 54     }
 55 
 56     /**
 57      * 校验列表索引越界
 58      * @param index
 59      */
 60     private void checkCapacity(int index){
 61         if (index > this.size - 1 || index < 0)
 62             throw new IndexOutOfBoundsException(new StringBuffer("[index : ").append(index).append("] , [size : ").append(size).append("] ").toString());
 63     }
 64 
 65     @Override
 66     public boolean isEmpty() {
 67         return this.size == 0;
 68     }
 69 
 70     @Override
 71     public void clear() {
 72         this.init(0);
 73     }
 74 
 75     @Override
 76     public E get(int index) {
 77         this.checkCapacity(index);
 78         return this.elementData[index];
 79     }
 80 
 81     @Override
 82     public int indexOf(E e) {
 83         for (int i = 0; i < this.size; i++){
 84             if (e == null && elementData[i] == null || e.equals(elementData[i])){
 85                 return i;
 86             }
 87         }
 88         return -1;
 89     }
 90 
 91     @Override
 92     public boolean contains(E e) {
 93         return this.indexOf(e) > 0;
 94     }
 95 
 96     @Override
 97     public E set(int index, E e) {
 98         this.checkCapacity(index);
 99         this.dilatation();
100         E oldElement = this.elementData[index];
101         this.elementData[index] = e;
102         return oldElement;
103     }
104 
105     @Override
106     public E remove(int index) {
107         this.dilatation();
108         E e = elementData[index];
109         if (index == size - 1) elementData[index] = null;
110         else {
111             int length = size - index - 1;
112             System.arraycopy(elementData, index + 1, elementData, index, length);
113         }
114         size --;
115         return e;
116     }
117 
118     @Override
119     public E add(E e) {
120         return this.add(size, e);
121     }
122 
123     @Override
124     public E add(int index, E e) {
125         this.dilatation();
126         if (index == size) elementData[index] = e;
127         else {
128             index++;
129             int lastLength = size - index;
130             E[] lastElementData = (E[]) new Object[lastLength];
131             System.arraycopy(elementData, index, lastElementData, 0, lastLength);
132             elementData[index] = e;
133             System.arraycopy(lastElementData, 0, elementData, index + 1, lastLength);
134         }
135         size ++ ;
136         return e;
137     }
138 
139     @Override
140     public int size() {
141         return this.size;
142     }
143 
144 }

View Code