机器学习中的规则化

Posted 2020-06-23 软件心理学工程师

　　最近重新看了《机器学习实战》第八章：预测数值型数据：回归。发现了一个以前没有重视的问题，规则化（regularization），通过网上各种查找资料，发现规则化对数据的特征选择，防止回归模型过拟合都有非常大的帮助。

　　简单的讲，规则化就是给损失函数（cost function）多项式再加上一项，使得训练出的权重向量W更小一些。这样，在向量W中，就会使得一些item更趋近于0，可以认为更趋近为0的项代表的维度对模型的分类预测效果影响很小，可以选择性的忽略这些维度。

　　能够从原始数据集中提取出影响较大的维度，忽略一些影响较小的维度，就意味着能够在一定程度上防止过拟合（overfitting）。为什么？因为模型兼顾的维度越多，越容易出错，这方面有个奥卡姆剃刀原理。

　　如何选择加上的那一项呢，常用的有L1,L2范数。

　　L1范数是指向量所有item的绝对值的和:

　　

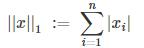
　　L2范数是指向量所有item的平方和开根号:

　　

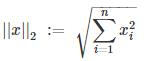
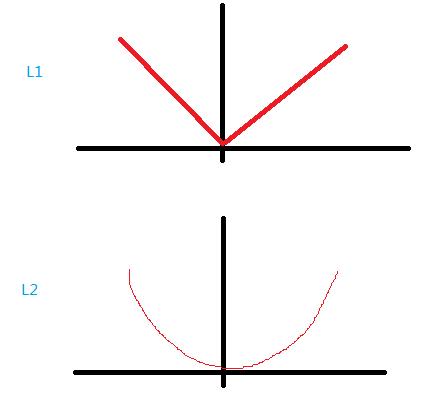
　　Spark针对不同的损失函数模型，赋予了默认的L1或L2规则化。为什么不同的模型对应不同的规则化呢，这个并不好解释，我个人觉得还是跟数据特征和先验积累有关。不过，只要了解L1和L2的不同之处，就能灵活运用。L1与L2主要的不同之处可以从变化曲线的斜率看出，L1是线性变化，L2是乘方变化的。